Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Попов Н.В. 1

---

1 ФГБОУ ВПО «Пермский государственный национальный исследовательский университет»

Одним из ключевых компонентов робототехники является искусственный интеллект. Робот должен имитировать психические функции людей, в частности, эмоции и память. Имитируемые роботом функции психики по своим характеристикам должны быть подобны человеческим: к примеру, робот c течением времени должен забывать прошлые события, поскольку память робота неабсолютна. Возникает потребность в формализации с помощью математики данных понятий и ряда других, вспомогательных, понятий, таких как эмоциональное воспитание. В статье изучена математическая модель эмоционального воспитания равномерно забывчивого робота. Доказано, что суммарное воспитание равномерно забывчивого робота всегда конечно. Найдены условия, при которых суммарное воспитание робота будет сходиться к определённому числу, то есть будет асимптотически устойчиво. Введён ряд характеристик предельного воспитания робота. Приведен пример реализации асимптотической устойчивости воспитания. Предложены идеи использования результатов статьи в моделировании эмоционального поведения роботов.

Статья в формате PDF

2800 KB

роботы

робототехника

эмоциональные роботы

эмоциональное воспитание

исследование

1. Андерсон Дж. Дискретная математика и комбинаторика. – М.: Вильямс, 2004. – 960 с.

2. Гипотезы и алгоритмы математической теории исчисления эмоций: монография / Перм. гос. ун-т; [под. ред. О.Г. Пенского]. – Пермь, 2009. – 152 с.

3. Пенский О.Г., Черников К.В. Основы математической теории эмоциональных роботов: монография / Перм. гос. ун-т. – Пермь, 2010. – 256 с.

4. Пенский О.Г. Математические модели эмоциональных роботов: монография / О.Г. Пенский. – Пермь: Перм. гос. ун-т, 2010. – 193 с.

5. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления: учеб. для вузов. – 8-е изд. – М.: ФИЗМАТЛИТ, 2001. – Т. 1. – 680 с.

6. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления: учеб. для вузов. – 8-е изд. – М.: ФИЗМАТЛИТ, 2001. – Т. 2. – 864 с.

7. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления: учеб. для вузов. – 8-е изд. – М.: ФИЗМАТЛИТ, 2002. – Т. 3. – 728 с.

8. Черников К.В. Математические модели роботов с неабсолютной памятью: дис. канд. физ.-мат. наук. – Пермь, 2013.

В математической теории эмоциональных роботов [2–4, 8] суммарное воспитание, полученное некоторым роботом в ходе воспитательного процесса, описывается формулой

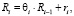
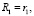
где под тактом понимаем время, в течение которого робот испытывает эмоции вследствие воспитательного воздействия [3]; ri –элементарное воспитание, полученное на i-м такте [3];

?i – коэффициент памяти для i-го такта (0 ? ?i < 1, память робота неабсолютна [8]); Ri – общее воспитание, приобрётенное роботом в течение i первых тактов [3].

Рассмотрим случай равномерно забывчивого робота 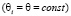[3, 4]. Суммарное воспитание такого робота описывается рекуррентным соотношением

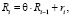
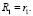(1)

Последовательность, задаваемую этой формулой, назовём неклассическим рядом. Отметим, что классический ряд 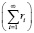[6], характеризуемый рекуррентным соотношением 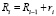, где 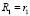, является частным случаем неклассического при ? = 1. Свойства классического ряда исчерпывающе описаны в фундаментальном труде по математическому анализу [5–7].

Целью предлагаемой статьи является изучение свойств неклассических рядов и нахождение критерия их сходимости.

Критерий сходимости неклассических рядов

Рассмотрим случай, когда последовательность 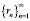– ограничена. Тогда выполняется следующая лемма.

Лемма. Если 0 ? ? < 1 и последовательность 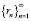– ограничена, то неклассический ряд 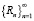– тоже ограничен.

Доказательство.

По условию леммы, найдется такое число m > 0, что 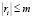для любого i. Докажем, что при сделанных предположениях 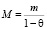ограничивает ряд 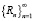, то есть, какой бы i ни взять, .

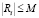Для i = 1 справедлива цепочка неравенств:

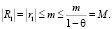
Пусть наше утверждение доказано для всех 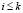, то есть 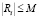для данных значений индекса. Истинность утверждения для 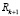следует из следующих соотношений:

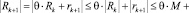
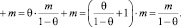
Таким образом, лемма доказана по методу математической индукции.

Следствие. Если 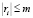при любом i, то 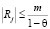для всех j (i и j – натуральные числа).

В рамках теории доказанная лемма говорит о том, что при ограниченных воздействиях на равномерно забывчивого робота его суммарное воспитание будет ограничено.

Предположим, что последовательность элементарных воспитаний робота 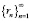при неограниченном возрастании n сходится к определённому пределу. При данном условии справедлива следующая теорема.

Теорема. Неклассический ряд 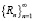при 0 ? ? < 1 сходится тогда и только тогда, когда последовательность 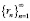имеет конечный предел при .

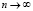Доказательство.

Необходимость.

Пусть 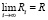. Запишем определение неклассического ряда и выразим оттуда 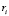: 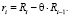Отсюда получаем

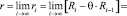
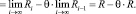
Следовательно, последовательность 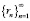сходится к числу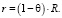

Достаточность.

Пусть 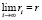и 0 ? ? < 1. Введём вспомогательные последовательности: 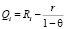, 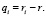Для введённых последовательностей задача переформулируется следующим образом: доказать, что для больших значений i величины 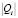оказываются меньшими любого наперёд заданного ? > 0. Заметим, что по свойствам пределов [5] qi – бесконечно малая величина.

По определению, 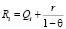, 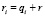. С учётом введённых обозначений преобразуем рекуррентную формулу (1):

,

.

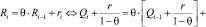
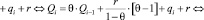
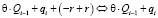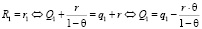Таким образом, мы получили следующее рекуррентное задание для ряда .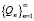

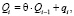
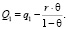
Поскольку, по свойствам пределов [5], сходящаяся последовательность 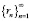– ограничена, мы можем применить лемму и сделать вывод о том, что ряд 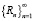, а вместе с ним и 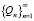ограничены. То есть найдется такое число M, не зависящее от i, что .

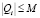Зададимся произвольным ? > 0 и введём в рассмотрение ?? – пока неизвестное для нас положительное действительное число. Подберём ?? по числу ? так, чтобы выполнялось 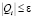, начиная с некоторого номера N. Тем самым мы установим сходимость ряда. Пусть Nq – натуральное число, такое, что для всех .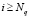

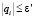Для частичных сумм неклассического ряда 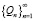, начиная с 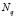справедливы следующие оценки сверху:

, ,

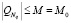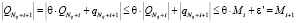где Mi – оценка сверху для величины,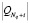

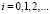
Таким образом, мы получили рекуррентно заданную последовательность:

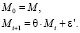
Решением полученной рекуррентной последовательности [1], удовлетворяющим начальному условию, является выражение

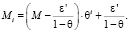
По условию, 0 ? ? < 1. А значит, 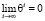. То есть по числу 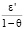(взято для удобства дальнейших выкладок) найдется такой номер N?, что для любого i ? N? справедливо неравенство 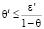. Отсюда, при условии 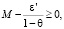следует истинность цепочки соотношений

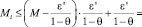
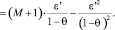(2)

Ниже будет показано, что искомый ?? обращает коэффициент при ?i в неотрицательное число, а значит, неравенство (2) верно. Используем соотношение (2) для определения значения ?? по известным и не зависящим от i величинам M, ?, ?. Таким образом, справедливо равенство

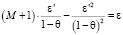. (3)

Ясно, что из наших рассуждений и равенства (3) при искомом значении ?? следует, что 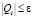, начиная с некоторого номера N (при этом легко видеть, что ).

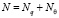Разрешив квадратное уравнение относительно ??, получаем равенство

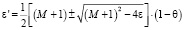. (4)

Потребуем для ?? выполнения следующих условий:

1) ?? – действительное число. А значит,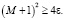

2) 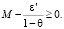Данное условие необходимо для справедливости оценки сверху, приведенной выше. После подстановки в это неравенство значения ??, определяемого формулой (4), и несложных преобразований получаем, что в соотношении (4) нужно выбрать знак «–» и .

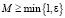Если M ? ?, то приведённые выше условия выполняются автоматически:

,

,

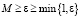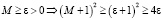так как .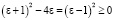

Поскольку, задавшись произвольным ?, в наших рассуждениях фактически не играла никакой роли величина M (существенным оставалось лишь то, что M ограничивает сверху ряд 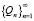), то систему условий можно заменить на одно, более простое, требование – M ? ? – и при необходимости можно увеличить M, чтобы данное требование выполнялось.

Подводя итог доказательству достаточности условий теоремы, сформулируем последовательность шагов для определения сходимости ряда :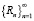

1. Возьмём некоторое положительное число ?.

2. Возьмём любое число M, удовлетворяющее следующим условиям:

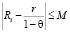? , независимо от i.

? M ? ?.

3. Вычислим

.

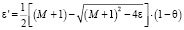4. Вычислим Nq: такой номер, что, каким бы ни был ,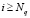

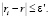
5. Вычислим N?: такой номер, что, каким бы ни был , .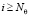

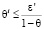6. Тогда 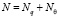, и, при любых ,

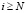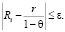
То есть 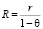– предел для ряда 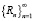по определению.

Следствие. Если 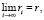то 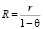– сумма неклассического ряда .

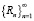Характеристики предельного воспитания робота

Согласно доказанному критерию, сходимость суммарного воспитания некоторого робота эквивалентна сходимости соответствующей последовательности элементарных воспитательных воздействий, оказанных на робота. В дальнейшем сходящуюся последовательность элементарных воспитаний будем называть планом воспитания, предельное значение суммарного воспитания – целью воспитания. Используя следствие из критерия сходимости, получаем соотношение между целью и планом воспитания:

,

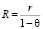где R – цель воспитания, 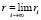, 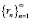– план воспитания, ? – коэффициент памяти робота [3].

На практике время, в течение которого воспитывался робот, всегда конечно. Поэтому существует потребность в вычислении времени (числа тактов), по прошествии которого цель воспитания будет достигнута с заданной точностью, при выбранном плане воспитания. Число тактов, достаточное для того, чтобы суммарное воспитание робота отклонялось от цели воспитания не более чем на заданную величину ?, назовём эффективным временем воспитания и обозначим ET(?). Вычислить ET(?), используя только план воспитания 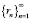и коэффициент памяти робота ?, можно, например, с помощью последовательности шагов, описанной выше. Из соображений удобства заменим второй пункт эквивалентной ему совокупностью действий:

2.1. Возьмём любое число m, такое, что 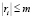для любых натуральных i.

2.2. .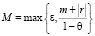

Число M, вычисленное предложенным способом, будет удовлетворять обоим условиям второго пункта:

,

.

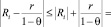
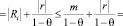
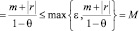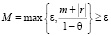Для первой цепочки неравенств использованы следствие из леммы для критерия сходимости неклассических рядов и соотношения для модулей действительных чисел.

Ясно, что при задании точности ? ~ 1 %, определяющей отклонение итогового воспитания от цели воспитания, воспитательные воздействия, начиная с ET(?) + 1-го, практически не возымеют на робота никакого эффекта.

Пример численной реализации критерия сходимости

Рассмотрим робота, коэффициент памяти [3] которого 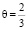. Пусть план воспитания подчиняется экспоненциальному закону ,

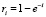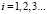
Поскольку 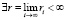, суммарное воспитание, полученное роботом, будет иметь конечный предел. Целью воспитания является .

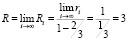Вычислим эффективное время воспитания, соответствующее точности ? = 10–2.

,

,

,

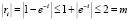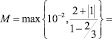
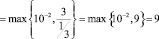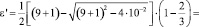
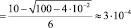(?? допустимо округлять вниз, так как из условия ? ? ?? следует справедливость цепочки неравенств 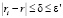и ),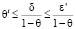

,

,

.

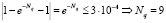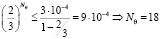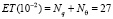Суммарное воспитание робота после двадцати семи тактов воспитательного процесса, вычисленное при помощи компьютера, составляет R ? 2,99993. Для этого числа порядок точности существенно больше, чем заданный. Объясняется это тем, что M значительно превосходит точную верхнюю грань [5] множества всех возможных значений величины .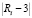

Заключение

Таким образом, в предложенной статье была исследована математическая модель суммарного воспитания равномерно забывчивого робота [3, 4, 8]. Результатом исследования стали критерий сходимости воспитательного процесса и ряд характеристик предельного воспитания робота.

Полученный критерий можно использовать в робототехнике для подбора параметров искусственного интеллекта робота, связанных с воспитанием, в частности, для того, чтобы гарантировать устойчивое воспитание робота, а значит, стабильную, предсказуемую реакцию робота на внешние воздействия. Свою ценность имеет и лемма, использованная для доказательства критерия: она фактически постулирует тот факт, что в модели роботов с неабсолютной памятью [8] воспитание, приобретённое роботом, всегда будет конечно, так как воздействия на робота ограничены. Численная характеристика эффективного времени воспитания может быть полезна при первичной «воспитательной» настройке робота при производстве, чтобы гарантировать поведение, близкое к тому, которое в идеале должно быть у робота, определяемое целью воспитания.

Библиографическая ссылка