Система образовательной подготовки специалиста в современном информационном обществе должна ориентироваться на формирование личности, способной к адекватной адаптации к быстроменяющимся информационным полям и технологиям, обладающей навыками самостоятельной постановки целей деятельности и планирования способов их достижения. Это с неизбежностью приводит к необходимости введения новых педагогических технологий и методик обучения, направленных на развитие творческой самостоятельности и познавательной активности студентов. В соответствии с этим нами предложен и апробирован ряд методов, позволяющих, по нашему мнению, усилить развивающий, креативный характер обучения. В частности, с целью развития творческих способностей, умения видеть и ставить проблему используются следующие методы организации креативной познавательной деятельности студентов:
1. Углубленный анализ решения задачи с исследованием возможностей получения дополнительной информации, обобщения и практического применения результатов.
2. Решение как известных, так и оригинальных качественных задач, задач-оценок и задач-проблем.
3. Анализ вопросов и задач по методологическим проблемам.
4. Самостоятельное составление и анализ вопросов и задач креативного характера.
На наш взгляд, решение задачи, пусть даже самое квалифицированное, т.е. ответ на вопрос в том виде, в котором он непосредственно сформулирован в задаче, не может являться самоцелью студента. Как правило, большинство задач, используемых на практических занятиях, составлено таким образом, что, помимо основного, можно задать и другие, не менее интересные вопросы, ответы на которые существенно расширяют научный кругозор студентов. Кроме того, почти всегда имеется возможность некоторого видоизменения условия задачи в рамках изучаемой темы. Это позволяет, во-первых, глубже понять суть изу чаемых явлений, во-вторых, вплотную подводит студентов к проблеме научного поиска. Таким образом, студенты не должны ограничиваться только решением задачи, а должны провести ее всесторонний анализ, причем как до, так и после решения. Схема анализа задачи, составленная на основе работ Д. Пойа [6] и Г.Е. Пустовалова, включает в себя следующие этапы:
1) идеализация условия;
2) проверка решения;
3) нахождение частных случаев;
4) формулирование дополнительных вопросов задачи;
5) видоизменение условия задачи;
6) обобщение решения задачи;
7) практическое применение решения задачи.
Проанализируем этапы решения задачи, выявив весь спектр познавательных способностей, развиваемых у обучающегося.
Идеализация условия. При анализе условия задачи необходимо обратить внимание на характер объектов. Если они реальны, то для них нужно выбрать подходящие физические модели (материальная точка, пробный заряд и т.д.). Выделяя главное свойство объекта в данном явлении и пренебрегая второстепенными, создают модель реального объекта, которая является уже новым, идеализированным объектом. Идеализация условия задачи учит видеть предмет во множестве его связей, выделять существенные и несущественные признаки явлений, главное, осознавать пределы применимости законов и формул, развивает понятие модели, абстракции, формирует исследовательские и методологические навыки. При соответствующей педагогической инструментовке этот этап используют для анализа расхождения теоретических и экспериментальных результатов.
Проверка решения. Проверка правильности решения позволяет углубить понимание смысла и значимости физических величин, обучает оценивать достоверность полученных результатов с физической и математической точки зрения.
Нахождение частных случаев. Нахождение частных случаев является одним из методов проверки правильности решения. А умение быстро и правильно дать оценку полученных результатов является необходимым качеством специалиста в современном мире больших и быстроменяющихся объемов информации. Во многих задачах решение можно расчленить на целый ряд частных случаев. Как правило, общее решение задачи не поддается непосредственной умозрительной интерпретации. Для того чтобы это решение стало более очевидным, необходимо попытаться представить его, пусть хотя бы и приблизительно, в виде совокупности некоторых частных решений. В некоторых случаях могут быть найдены еще неизвестные частные случаи, анализ которых способствует углублению знаний. Поэтому нахождение частных случаев является важным этапом анализа задачи.
Формулирование дополнительных вопросов задачи. В центре современных дидактических концепций, ориентированных на развитие способности действовать, стоит формирование способности к приобретению знаний, что, в свою очередь, предполагает умение спрашивать. Любое познание начинается с вопроса, решение вопроса – это путь к знанию. Еще И. Кант среди методов развития человеческих способностей выделял искусство задавать вопросы и находить на них правильные ответы: «Умение ставить разумные вопросы есть уже важный и необходимый признак ума или проницательности» [5]. классик герменевтики ХХ века Х.-Г. Гадамер отмечал: «Искусство вопрошания и есть, собственно, искусство мышления» [1]. умение человека задавать правильные вопросы является одним из базовых умений как для учения, так и для будущей профессиональной деятельности. При этом «понимание вопроса часто важнее, чем знание ответа» [7]. Однако анализ психолого-педагогической литературы и собственный опыт работы позволяют сделать вывод о том, что умение задавать и формулировать вопросы является одним из наиболее слабо сформированных умений и навыков студентов; в лучшем случае сформулированный вопрос соответствует первому уровню воспроизведения знаний. Между тем современный специалист должен обладать хорошими адаптационными способностями в условиях необходимости быстрого принятия решений, для этого ему нужно уметь видеть весь спектр потенциальных возможностей анализируемой ситуации, поэтому этап формулирования дополнительных вопросов задачи развивает мыслительные способности на втором и третьем уровнях, т.е. позволяет применить знания как в знакомой ситуации, так и в незнакомой. Почти во всех задачах выносимый для ответа вопрос не является единственным вопросом, который может быть задан, исходя из условия задачи. Дополнительные вопросы, которые могут формулировать студенты, способствуют формированию у студентов навыков исследовательской работы и развитию умения квалифицированно задавать вопросы, выделять главное в изучаемом материале, ставить цели и задачи деятельности и планировать работу по их решению. При этом у студентов повышается гибкость и подвижность мышления, снижается стереотипность способов мышления, развивается способность одновременно ставить и решать проблемы. Кроме того, подобные вопросы могут направлять студентов в русло их индивидуальных научных интересов.
Видоизменение условия задачи. Самостоятельность в решении задач на занятиях должна простираться, на наш взгляд, вплоть до видоизменения, разумеется, квалифицированного, условия задачи. Это должно позволить учащимся гораздо глубже проникнуть в суть явления. При таком подходе обнаруживается не «застывший», раз и навсегда данный характер задачи, а ее динамический, «живой», приближенный к реальности смысл.
Обобщение решения задачи. Важным этапом анализа задачи является ее обобщение, что весьма эффективно способствует умению систематизировать знания по какой-либо теме или разделу курса, требует от студента активной работы мысли, формирует фундаментальные физические понятия, позволяет оценить значимость полученных знаний, испытать чувство удовлетворения. На данном этапе акцент надо делать не на вопрос задачи, а на то, о каких явлениях идет речь, каковы объекты задачи в наиболее общем виде, и как они могут вести себя в других случаях. Обобщенное решение может отчетливо выявить нетривиальный набор тех законов, принципов и определений, с помощью которых могут быть описаны рассматриваемые в задаче явления. Оно также весьма эффективно способствует закреплению теоретического материала.
Практическое применение решения задачи. Практическое применение результатов любой задачи стимулирует к неформализованному решению задачи, пробуждает живой интерес к самому предмету, способствующий развитию чрезвычайно важных для специалиста прикладных способностей.
Приведем несколько конкретных примеров.
Задача № 1 [4]. Два небольших одинаково заряженных шарика, каждый массой m, подвешены в одной точке на шелковых нитках длиной l. Расстояние между шариками ![]() . Найти скорость утечки зарядов dq/dt каждого шарика, если скорость их сближения меняется по закону
. Найти скорость утечки зарядов dq/dt каждого шарика, если скорость их сближения меняется по закону ![]() , где с – постоянная.
, где с – постоянная.
Не останавливаясь на методе решения задачи, не являющемся предметом рассмотрения в данной статье, приведем сразу решение:
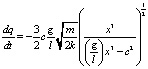 .
.
Анализ показывает, что диапазон расстояний, в котором справедливо полученное решение, определяется неравенством
![]()
Отсюда сразу дополнительный вопрос: чем физически обусловлены такие ограничения на расстояние между заряженными шариками? В анализе данной задачи наибольший интерес представляет формулирование дополнительных вопросов, неполный перечень которых приведем ниже.
Как изменяется расстояние между шариками со временем? Каков характер этого изменения? Как изменяется со временем величина заряда каждого из шариков? Чему равны напряженность и потенциал электрического поля в точке, лежащей на прямой, соединяющей шарики? Как изменяется с течением времени сила электрического взаимодействия заряженных шариков? Как изменяется со временем полная энергия шариков? Из чего она складывается? Каковы физические механизмы, обуславливающие возможность утечки заряда с шариков? Чему равна величина тока утечки? Чему равна при заданных условиях задачи удельная проводимость окружающей среды? Каково полное сопротивление утечки? По результатам расчета, сопротивление среды является переменным. Какой физический механизм может обусловить изменяющееся с течением времени сопротивление утечки? Полный анализ задачи приведен в разработанном нами учебном пособии [3].
Задача 2 [4]. Кольцо радиуса R из тонкой проволоки имеет заряд Q. Найти модуль напряженности электрического поля в точке А, лежащей на оси кольца Оy на некотором расстоянии y от его центра.
При идеализации условия толщиной проволоки пренебрегаем, распределение заряда по кольцу считаем равномерным, заряд кольца принимаем положительным. В этом случае решение имеет вид: вектор напряженности электрического поля, создаваемого кольцом, в точке А направлен вдоль оси симметрии кольца, а его модуль равен
![]() .
.
При анализе частных случаев интерес представляет вывод о том, что при у = 0, т.е в центре симметрии кольца, получаем E = 0. Опираясь на условие задачи, можно найти еще потенциал в точке А; графически изобразив зависимость Е(у), можно установить, что эта зависимость имеет экстремальный характер. Следовательно, можно найти максимальное значение Еm и координату точки ym, в которой этот максимум достигается.
Большой интерес в задаче представляет видоизменение условий задачи.
Предположим, что в точку А помещен точечный положительный заряд q. Массой заряда пока пренебрегаем. В этом случае можно рассмотреть целый ряд вопросов. В частности: чему равна электрическая энергия полученной системы? Какая сила действует на заряд q? Так как сила, действующая на заряд, имеет экстремальный характер и при у = 0 равна 0, то отсюда следует нетривиальный вывод: в определенном диапазоне расстояний (в данном случае 0<|y|<|ym|) при уменьшении расстояния между одноименно заряженными телами сила отталкивания между ними также уменьшается! Следующий вопрос: как движется положительный точечный заряд, помещенный в точку А, под действием сил электрического поля, создаваемого зарядом кольца? Считаем, что масса заряда т. Заряд будет двигаться вдоль оси Оу с положительным ускорением, величина которого переменна. При этом скорость заряда все время нарастает, до точки у = уm быстро, затем все медленнее, и заряд неограниченно удаляется от кольца. До каких пор происходит нарастание скорости заряда q? Как известно, скорость материального тела не может превышать скорости света. Что же ограничивает нарастание скорости заряда q?
Теперь предположим, что в точку А помещен точечный отрицательный заряд, масса которого т. Очевидно, что модуль силы, действующей на него, и электрическая энергия системы «кольцо-заряд» будут определяться соотношениями, полностью аналогичными полученным в случае положительного заряда. Какой характер имеет движение этого заряда? Анализ показывает, что движение заряда представляет собой механические колебания вдоль оси Oy с центром в точке О. Какой характер имеют механические колебания заряда q? Каков период этих колебаний? Какую максимальную скорость может приобрести заряд q, помещенный в точку А?
Интерес представляет и обобщение решения задачи. Если вместо проволочного кольца рассмотреть любую проволочную фигуру, обладающую осью симметрии, то качественно зависимость Е(у) будет иметь вид, аналогичный рассмотренному выше. Из этого можно сделать следующие выводы:
1. Изменение напряженности электрического поля, создаваемого заряженной симметричной проволочной фигурой вдоль оси фигуры, имеет экстремальный характер.
2. Напряженность электрического поля в центре симметрии проволочной фигуры равна нулю.
3. Если точечный заряд находится на оси симметричной проволочной фигуры, то при 0<|у|<|уm| при сближении заряженных тел сила взаимодействия между ними уменьшается, достигая нуля в центре симметрии проволочной фигуры.
Справедливы ли сделанные нами выводы для сплошных тел, имеющих ось симметрии?
Можно проанализировать и практические приложения этой задачи. В частности, систему, аналогичную рассмотренной в задаче, можно использовать для фокусировки пучков заряженных частиц; для разделения разноименно заряженных частиц; для сортировки заряженных частиц по массе.
Полный анализ задачи приведен в разработанном нами учебном пособии [3].
Накопленный в процессе применения методики решения задач с расширенным анализом опыт позволяет заключить, что достигается несколько целей обучения. Происходит углубление и расширение знаний, так как для того, чтобы провести хороший анализ, необходима основательная проработка материала по теме, внимательное изу чение как основной, так и дополнительной литературы, что способствует развитию навыков работы с научной литературой. А это является одним из основных видов самостоятельной учебной работы студентов. При этом растет интерес не только к самому содержанию изучаемого материала, но и улучшается психоэмоциональное состояние студентов, так как сам процесс анализа, особенно составления вопросов, вызывает заинтересованность у абсолютного большинства студентов, стимулирует интерес к учебе, к овладению знаниями и расширению их спектра. Поиск ответов на возникшие и сформулированные вопросы способствует формированию навыков самостоятельного поиска нужной информации и умения с ней работать, что подразумевает развитие умений самостоятельной постановки целей деятельности. Проработанный таким образом материал усваивается глубоко и надолго, а объем информации, получаемой студентами, намного расширяется по сравнению с обычно получаемой и изучаемой. При этом студенты учатся видеть проблемные аспекты, казалось бы, привычных утверждений, анализировать явление, утверждение с различных сторон, выявлять скрытые потенциальные возможности, заложенные в том или ином тексте (здесь текст понимается в смысле методологии гуманитарного познания, т.е. текст – это утверждение, формула и т.д.). Умение видеть в привычном, обыденном новые грани и возможности способствует развитию общей креативности, что ценится в любой области деятельности. При использовании этого метода формируются такие элементы творческой деятельности, как самостоятельный перенос знаний и умений в новую ситуацию, видение задачи в знакомой ситуации, выявление новой функции и структуры объекта, самостоятельное комбинирование из известных способов деятельности нового, альтернативный подход к поиску решения проблемы. А способность к обнаружению и самостоятельной постановке проблем, способность решать проблемы, умение делать выводы, умозаключения, устанавливать причинно-следственные связи, сравнивать и обобщать, т.е. способность к анализу и синтезу и некоторые другие факторы, объединенные Дж. Гилфордом в понятии «дивергентное мышление» [2], отражают познавательную сторону креативности. Мы считаем, что рассмотренный метод может быть полезен не только в процессе обучения, но и в различных сферах будущей профессиональной и социальной деятельности студентов.
Библиографическая ссылка
Елканова Т.М. РЕШЕНИЕ ЗАДАЧ КАК МЕТОД РАЗВИТИЯ КРЕАТИВНОСТИ // Современные наукоемкие технологии. 2015. № 12-2. С. 317-321;URL: https://top-technologies.ru/ru/article/view?id=35262 (дата обращения: 12.03.2026).



