При решении задач анализа и синтеза систем управления манипуляционными роботами (МР) требуется решать задачи кинематики и динамики. Различается прямая и обратная задача кинематики. Прямая задача кинематики (ПЗК) состоит в определении пространственного положения и ориентации характерной точки, как правило, схвата МР по известным значениям обобщенных координат. Обратная задача кинематики (ОЗК), как и прямая задача, является одной из основных задач кинематического анализа и синтеза манипуляторов. Управление МР, как правило, осуществляется в пространстве обобщенных координат (ОК), а координаты схвата МР задаются в некоторой базовой координатной системе. Таким образом, для управления положением звеньев и ориентацией схвата МР возникает необходимость решения ОЗК [3–5].
Формулировка ОЗК
По заданному (6×1) вектору линейных координат положения и угловых координат ориентации схвата МР
вычисляется (n×1) вектор обобщенных координат звеньев:
,
где xc, yc, zc – пространственные координаты положения схвата МР, φc, θc, ψc – угловые координаты ориентации схвата МР, qi, i = 1…n – обобщенные координаты звеньев МР [1].
Как правило, ОЗК оказывается более сложной по сравнению с прямой. Это объясняется следующим: при решении ОЗК может возникнуть кинематическая неопределенность, когда для одного и того же положения схвата может существовать две или более конфигураций манипулятора, т.е. для одного вектора линейных координат положения и угловых координат ориентации схвата Sc может существовать несколько наборов ОК q, и в результате задача решается неоднозначно. На практике для выбора однозначного решения ОЗК обычно используют дополнительные условия, такие как, ограничения в кинематических парах, учет препятствий в зоне обслуживания и др.
Методы решения ОЗК для МР можно разделить на точные (аналитические) и приближенные (итерационные).
В результате использования точных методов вектор ОК удается получить в виде аналитической зависимости геометрических параметров кинематической схемы МР. В этом случае процесс нахождения искомого вектора ОК по вектору положения и ориентации схвата МР при известной кинематической схеме сводится к вычисления значений заранее полученных аналитических зависимостей. Однако, нахождение точного решения в виде аналитических зависимостей для ОК от конструктивных параметров и заданного вектора положения манипулятора представляется возможным не для всех МР, а для определенных кинематических схем манипулятора.
В современной робототехнике наиболее широкое распространение при использовании аналитических методов решения ОЗК получили метод обратных преобразований и геометрические методы. Метод обратных преобразований позволяет решать ОЗК простых манипуляторов. Суть метода заключается в определении углов поворотов звеньев из уравнений для отдельных элементов имеющегося матричного уравнения [3]. Геометрический подход связан с использованием для нахождения аналитического решения ОЗК особенностей кинематической схемы МР. Данный способ, рассмотренный на примере шестизвенного МР типа PUMA, подробно описан в [3, 9]. К недостаткам аналитического решения ОЗК относятся сложность получения ОК в явном виде и неопределенность, связанная с кинематической неоднозначностью и используемыми тригонометрическими функциями.
В случае если решение ОЗК в виде аналитических выражений невозможно, используются приближенные методы. Приближенные методы – это методы численного решения уравнений связи. Они оказываются работоспособными для любых кинематических схем. Однако это связано с использованием рекуррентных процедур. Среди них можно выделить группу методов, основанных на использовании матрицы Якоби: метод Ньютона, метод Гаусса-Ньютона, метод Левенберга-Марквардта [1]. Приближенные методы позволяют решить ОЗК для тех конструкций МР, для которых получение точного решения в аналитических выражениях не представляется возможным либо достаточно затруднительно. Однако, использование приближенных методов в режиме реального времени затруднено в связи с тем, что время сходимости того или иного метода заранее неизвестно.
Альтернативным подходом к решению ОЗК является аппроксимация соотношений, связывающих обобщенные координаты МР и координаты схвата и ориентации для заданных конфигураций МР. Данный подход целесообразно применять тогда, если классические подходы труднореализуемы.
Рис. 1. Промышленный манипулятор KUKA KR16
В качестве примера рассмотрим МР KUKA KR16 (рис 1). Роботы этой серии активно используются в российском промышленном производстве, в частности, на автомобилестроительных и авиастроительных заводах. Анализ приведенных в [6, 8] аналитических соотношений, связывающих обобщенные координаты МР KUKA KR16 и координаты схвата и ориентации, показывает их высокую вычислительную сложность, что связано с вычислениями тригонометрических зависимостей (например, операций вычислений sin и cos требуется более 70 раз). Это затрудняет реализацию предлагаемых алгоритмов на базе простых микроконтроллерных элементов. Значительное упрощение и снижение вычислительной сложности может быть обеспечено аппроксимацией исходных соотношений в контексте решения ОЗК с помощью классической многослойной нейронной сети. В работе [7] приведен обзор современных направлений в нейросетевой аппроксимации ОЗК, связанных с использованием многослойной нейронной сети прямого распространения (МНС) и сетей с радиально-базисными активационными функциями (РБФ-сети).
Многослойная нейронная сеть
Существует множество определений термина «нейронная сеть», но в первую очередь необходимо отметить, что нейронная сеть – это функция, графически представляемая в виде многослойной структуры. По аналогии с любой функцией, НС характеризуется входными аргументами (вектором входных значений), который при прохождении через нейросетевую структуру преобразуется в выходные значения (вектор выходных значений).
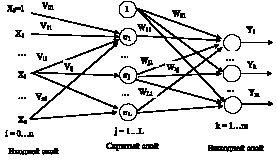
На рис. 2, а представлена схема трехслойной НС с одним скрытым слоем. На рис. 2, а приняты обозначения: Хi, 
– входные сигналы; Vij – весовой коэффициент между j-м нейроном скрытого слоя и i-м нейроном входного слоя; σj – выход j-го нейрона скрытого слоя; Wkj – весовой коэффициент между k-м нейроном выходного слоя и j-м нейроном скрытого слоя; Yk – выход k-го нейрона выходного слоя.
а б
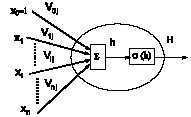
Рис. 2. а – сеть прямого распространения с одним скрытым слоем нейронов, б – модель искусственного нейрона
На j-й нейроподобный элемент поступает вектор входных сигналов 
, представляющий собой, в частном случае, выходные сигналы (значения активностей) других нейроподобных элементов, сигнал x0 = 1 представляет собой искусственно введенное смещение (англ. bias). Каждый входной сигнал линейно комбинируется с соответствующим весовым коэффициентом 
. Полученное значение определяет так называемый уровень возбуждения j-го нейрона hj:
. (1)
Величина активности j-го нейрона Hj определяется путем нелинейного преобразования уровня возбуждения hj нелинейным элементом, характеризующимся функцией преобразования σ(.):
. (2)
Для приведенной на рис. 1, а МНС выражение для выхода определяется соотношением:
, (3)
где 
– матрица весовых коэффициентов, связывающая нейроны скрытого слоя и нейроны входного слоя, столбцами матрицы являются весовые коэффициенты между нейронами скрытого слоя и входными нейронами; 
– матрица весовых коэффициентов, связывающая нейроны выходного слоя и нейроны выходного слоя.
Нейросетевая идентификация ОЗК
Рассмотрим алгоритм решения задачи нейросетевого моделирования обратной задачи кинематики в среде Matlab. Решение состоит из нескольких этапов.
1-й этап. Создание обучающей выборки. Для этого задаемся набором векторов, определяющих положение и ориентацию схвата МР 
, и, решая аналитически ОЗК, находим для каждого вектора Sc соответствующий вектор обобщенных координат 
, (n = 6). Математическая модель манипулятора KUKA KR-16, описывающая кинематические соотношения, приведена в [6, 8].
2-й этап. Создаем нейронную сеть. Для решения была выбрана трехслойная НС, имеющая по шесть входов и выходов, с сигмоидальной функцией преобразования в первом и втором слоях и линейной функцией – в третьем.
3. Последовательно предъявляя НС пары векторов из обучающей выборки, проводим обучение НС (для обучения использовались функции Matlab).
На рис. 3 приведена блок-схема алгоритма решения задачи нейросетевого моделирования обратной задачи кинематики.
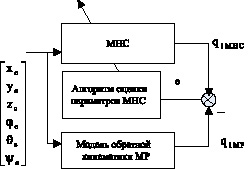
Рис. 3. Блок-схема алгоритма решения задачи нейросетевого моделирования обратной задачи кинематики
При проведении численного моделирования была проведена серия экспериментов, отличающиеся объемом выборки (от 100 до 1000 векторов), количеством итераций обучения. Ошибка обучения для многомерного выхода НС составила ~ 10-3, что приемлемо для поставленной задачи. Таким образом, проведенные численные эксперименты показали высокую эффективность предложенного метода нейросетевого моделирования обратной задачи кинематики.
Заключение
Одной из задач эффективного управления промышленными манипуляторами является решение задач кинематики. Обратная задача кинематики состоит в определении обобщенных координат робота, соответствующих заданному пространственному положению и ориентации схвата манипулятора. В связи с тем, что большинство известных аналитических подходов для решения ОЗК являются достаточно затратными с точки зрения вычислительных процедур, предложено использование альтернативного подхода, связанного с использованием многослойных нейронных сетей.
Работа поддержана Министерством науки и образования Российской Федерации, Государственный контракт 02G25.31.0025.
Библиографическая ссылка
Оськин Д.А., Дыда А.А., Константинова Е.А. НЕЙРОСЕТЕВОЕ МОДЕЛИРОВАНИЕ ЗАДАЧИ ОБРАТНОЙ КИНЕМАТИКИ ДЛЯ МАНИПУЛЯЦИОННОГО РОБОТА // Современные наукоемкие технологии. – 2015. – № 12-2. – С. 254-257;URL: https://top-technologies.ru/ru/article/view?id=35248 (дата обращения: 19.04.2024).