Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Дыда А.А. 1, 2 Оськин Д.А. 1, 2

---

1 Дальневосточный федеральный университет

2 Морской государственный университет имени адмирала Г.И. Невельского

В работе рассмотрен подход к построению системы управления электроприводом манипуляционного робота, основанный на принципах теории систем с переменной структурой, оптимального управления и адаптации. Особенностями динамики манипуляционных роботов является их нелинейность, многомерность и параметрическая неопределенность. Вследствие этого решение задачи синтеза систем управления для манипуляционных роботов имеет достаточно высокую сложность. Один из подходов, позволяющих упростить решение задачи синтеза, основан на декомпозиции сложной динамической системы на взаимодействующие подсистемы меньшей размерности. При этом взаимовлияние подсистем интерпретируется как внешнее возмущение. В статье предложены простые нелинейные регуляторы на базе систем с переменной структурой с адаптивной настройкой по параметру скольжения. Приводятся и обсуждаются результаты математического моделирования.

Статья в формате PDF

1947 KB

манипуляционный робот

субоптимальное управление

скользящий режим

1. Дыда А.А. Адаптивное и нейросетевое управление сложными динамическими объектами. Владивосток: Дальнаука, 2006. – 149 с.: 34 ил. – ISBN 978-5-8044-0811-5.

2. Павлов А.А. Синтез релейных систем, оптимальных по быстродействию. Метод фазового пространства. – М: Наука, 1966. – 392 с.

3. Теория систем с переменной структурой. / Под ред. Емельянова С.В. – М.: Наука, гл. ред. физ.-мат. лит., 1970. – 592 с.

4. Уткин В.И. Скользящие режимы в задачах оптимизации и управления. – М: Наука., гл. ред. физ.-мат. лит., 1981. – 368 с.

5. Фу К., Гонсалес Р., Ли К. Робототехника. Пер. с англ. под ред. В.Г. Градецкого. – М.: Мир, 1989. – 624 с.

6. Юревич Е.И. Основы робототехники: учеб. для вузов. – СПб.: БХВ-Петербург, 2005. – 416 с.

7. Dyda A.A., Oskin D.A., Longhi S., and Monteri? A. (2015), An adaptive VSS control for remotely operated vehicles. Int. J. Adapt. Control Signal Process., doi: 10.1002/acs.2565.

Производительность робототехнических систем в определяющей степени зависит от характеристик используемых приводов. Задача синтеза систем управления приводом манипуляционного робота (МР) является достаточно сложной. Это объясняется спецификой манипуляторов как объектов управления. Характерное для МР изменение полезной нагрузки и пространственной конфигурации ведет к существенным вариациям внешних моментов сил и моментов инерции, приведенных к валу исполнительного привода [5, 6].

В настоящей работе исследуется возможность построения простой нелинейной системы управления приводом МР, совмещающей в себе принципы и теорию систем с переменной структурой, оптимального управления и адаптации.

На рис. 1 представлена структурная схема привода МР, построенного на базе электродвигателя постоянного тока с независимым возбуждением (ДПТ НВ).

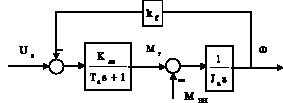
Рис. 1. Модель привода МР на базе электродвигателя постоянного тока

На рисунке приняты обозначения: Ua (В) – напряжение якорной цепи, KДВ = kf/Ra – коэффициент передачи двигателя, kf – конструктивный коэффициент двигателя, Ra (Ом) – сопротивление и индуктивность La (Гн) якорной цепи, Ja (кг·м2) – момент инерции ротора двигателя (с приведенной нагрузкой), MBH – внешний момент (Н·м), w (рад/сек) – угловая скорость вращения ротора. В ходе работы МР параметр Ja и внешний момент MBH существенно изменяются, в частности, из-за изменения конфигурации манипулятора и нагрузки в его схвате.

Естественным требованием к приводам МР является их высокое быстродействие, следствием чего является высокая производительность оборудования. Из теории оптимального управления следует, что максимальное быстродействие системы достигается при экстремальных значениях сигнала управления. Точное решение задачи синтеза системы управления МР, обеспечивающей максимальное быстродействие, едва ли возможно из-за нелинейной и многомерной динамики робота.

Поэтому поставим задачу приближенного субоптимального решения на основе декомпозиции сложной динамики МР на сепаратные взаимодействующие подсистемы.

Синтез нелинейного управления

Анализ систем оптимального управления показывает, что оптимальные по быстродействию траектории составлены из участков, соответствующих экстремальным значениям сигнала управления. Финальная часть траектории, построенной в фазовом пространстве, как правило, имеет вид параболической кривой, проходящей через начало координат.

Это соображение мотивирует нас выбрать закон децентрализованного управления приводом МР в виде

, (1)

где функция переключения может быть как линейной

, (2)

так и нелинейной

, (3)

где ei,  – соответственно, величина рассогласования и её производная.

Подобно системам с переменной структурой (СПС), в оптимальных системах могут возникать скользящие режимы [2–4], которые связаны с быстрыми переключениями управляющего сигнала и движением системы вдоль искусственной траектории (линии скольжения). Среднее значение переключаемого сигнала (эквивалентное управление Uэкв) определяет скорость движения системы в скользящем режиме. Близость модуля средней составляющей к экстремальному значению сигнала управления U0 характеризуется так называемым параметром скольжения μ, причем 0 ≤μ ≤ 1. Фактически, μ соответствует скважности прямоугольных импульсов на выходе релейного элемента sign(si) при возникновении скользящего режима. Можно показать, что Uэкв связано с μ следующим соотношением – Uэкв = U0(1 – 2μ). Граничные значения μ соответствуют Uэкв = U0 и Uэкв = – U0, т.е. максимально эффективному использованию сигнала управления.

Предположим, что выбор параметров функции переключения (2) обеспечивает возникновение скользящего режима вдоль линии si = 0 в подсистеме управления конкретной степени подвижности МР при наименее благоприятных значениях внешнего момента (максимальным и противодействующим) и максимальным моментом инерции.

Тогда при более благоприятном сочетании значений MBH и Ja (например, за счет изменения конфигурации манипулятора) скольжение вдоль si = 0 обеспечивается меньшим значением Uэкв, что проявляется в изменении параметра скольжения μ. Отмеченные свойства могут быть использованы для повышения скорости скользящих режимов за счет адаптивной подстройки параметров линии переключения [1, 7].

Суть предлагаемого алгоритма адаптивной настройки состоит в том, чтобы путем настройки параметров линии переключения добиться стремления текущего измеряемого параметра μ(t) к эталонному значению μэтал, которое выбирается близким к своему экстремальному значению.

Такая настройка обеспечивает близость Uэкв к экстремальным значениям управляющего сигнала U0 и, следовательно, максимально эффективной финальной стадии движения системы. В результате изображающая точка системы попадает в начало координат фазового пространства по траектории, близкой к оптимальной по быстродействию.

На рис. 2 приведена обобщенная структурная схема подсистемы управления i-м приводом МР. Здесь φi, φiж – соответственно фактическое и программное значение выходной координаты.

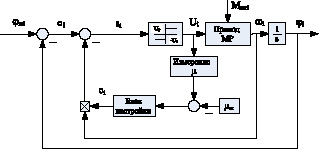
Рис. 2. Обобщенная структурная схема подсистемы управления приводом МР

Настройка коэффициента сi может быть выполнена, например, в соответствии с законом [1, 7]:

. (4)

Суть алгоритма настройки состоит в том, что линия скольжения поворачивается (деформируется) до тех пор, пока текущее значение μ(t) не станет близким к заданному значению μэт, при этом .

На рис. 3 и 4 приведены графики переходных процессов и фазовые траектории. На графиках цифрами 1 и 2 обозначены соответствующие постоянному и адаптивно настраиваемому значению коэффициента сi.

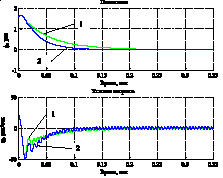
1) 2)

Рис. 3. Переходные процессы 1) и фазовые траектории 2) в СПС с линейной функцией переключения (2)

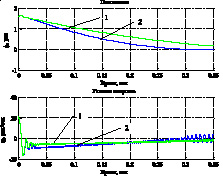
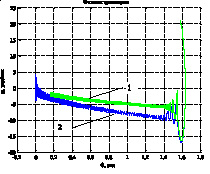
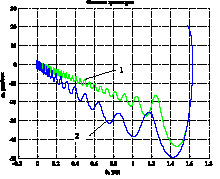
1) 2)

Рис. 4. Переходные процессы1) и фазовые траектории 2) в СПС с нелинейной функцией переключения (3)

Результаты моделирования показывают, что при адаптивной настройке параметра ci (процесс настройки приведен на рис. 5) линия скольжения поворачивается (деформируется) в область более высоких скоростей протекания переходных процессов. При этом параметр скольжения m стремится к своему экстремальному значению, а средняя составляющая сигнала управления Uэкв стремится к максимальному по модулю значению.

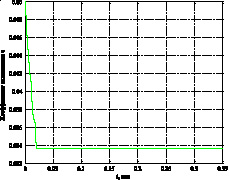
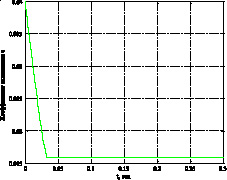
1) 2)

Рис. 5. Процесс настройки параметра скольжения ci для линейной 1) и нелинейной2) функции переключения

Заключение

Предложенный алгоритм децентрализованного управления приводом манипуляционного робота прост в реализации и сочетает в себе принципы СПС, оптимального и адаптивного управления. В отличие от стационарных линий скольжения в традиционных СПС, в предложенном алгоритме и системе управления выполняется адаптивная настройка параметров линии переключения, позволяющая повысить эффективность использования управляющего сигнала и, как следствие, повысить быстродействие системы.

Работа поддержана Министерством науки и образования Российской Федерации, Государственный контракт 02G25.31.0025.

Библиографическая ссылка