Огромные волны цунами, которые неожиданно обрушиваются на прибрежные города морей и океанов, являются одним из наиболее опасных и катастрофических явлений природы. Вдали от береговой линии эти волны не представляют никакой опасности, так как их высота редко превышает 1 метр. Но при входе волны в зону мелководья скорость переднего фронта волны резко уменьшается, а высота волн увеличивается в десятки раз. Ясно, что изучать волну цунами в натурных условиях практически не представляется возможным. Поэтому при исследовании волны цунами широко используют аналитические методы исследования, а также методы численного (компьютерного) моделирования и эксперименты в наземных установках [1–3].
В работе [4] была предложена математическая модель и ее программная реализация для комплексного исследования проблем волн цунами в гидродинамическом лотке. Проведена ее верификация, которая показала хорошее согласование численных расчетов с экспериментальными данными, полученными в лабораторной установке [3, 4]. Эксперименты проводились в 15-метровом гидродинамическом лотке ИПРИМ РАН, в котором генерировалась гравитационная волна длиной ? = 3 м и средней амплитудой A от 4,5 до 10 мм. Начальная глубина воды в лотке Н изменялась от 100 до 103 мм. При этом измеренная скорость распространения волн в лотке соответствовала теоретической в приближении «мелкой воды» (? >> H): 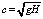 = 1,0003 м/с. В частности, в работе [4] показано, что при исследовании коэффициентов отражения волн от одиночной преграды данные экспериментов и численного моделирования при А/Н < 0,1 обобщаются единой зависимостью, но сильно отличаются от расчетной зависимости по линейной теории длинных волн. В работе [5] предложен безразмерный параметр преграды h/(H + A), учитывающий амплитуду падающей волны и высоту преграды h, относительно которого данные обобщаются в более широком диапазоне А/Н < 0,3. Установлено, что при определенных условиях вблизи тонких и непроницаемых подводных преград образуются крупномасштабные вихревые структуры, которые аккумулируют значительную часть энергии падающей волны. При значениях параметра h/(H + A) ? 0,8 – 0,9 энергия, сосредоточенная в вихревых структурах, имеет максимум, при этом энергия прошедшей через преграду волны может быть уменьшена почти вдвое относительно падающей волны [5, 6].
= 1,0003 м/с. В частности, в работе [4] показано, что при исследовании коэффициентов отражения волн от одиночной преграды данные экспериментов и численного моделирования при А/Н < 0,1 обобщаются единой зависимостью, но сильно отличаются от расчетной зависимости по линейной теории длинных волн. В работе [5] предложен безразмерный параметр преграды h/(H + A), учитывающий амплитуду падающей волны и высоту преграды h, относительно которого данные обобщаются в более широком диапазоне А/Н < 0,3. Установлено, что при определенных условиях вблизи тонких и непроницаемых подводных преград образуются крупномасштабные вихревые структуры, которые аккумулируют значительную часть энергии падающей волны. При значениях параметра h/(H + A) ? 0,8 – 0,9 энергия, сосредоточенная в вихревых структурах, имеет максимум, при этом энергия прошедшей через преграду волны может быть уменьшена почти вдвое относительно падающей волны [5, 6].
Авторы работы [9] в 5-метровом гидродинамическом лотке исследовали возможность подавления волн цунами двойными подводными преградами. Важным результатом этой работы является то, что расстояние между преградами ? и при значениях ?<<? влияет на высоту (и энергию) проходящей волны, причем существует минимум высоты берегового заплеска при определенных расстояниях между преградами. Объяснение этому эффекту до сих пор отсутствовало.
В данной работе авторами приведены результаты численного моделирования взаимодействия волн типа цунами с двойными преградами (рис. 1) при оптимальном [5] значении параметра h/(H + A) ? 0,84 для обеих преград. Толщина преград В = 10 мм, первая преграда располагалась на расстоянии 9 м от начала лотка, расстояние между преградами изменялось от 50 до 721 мм.
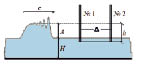
Рис. 1. Схематический чертеж численных экспериментов с двумя преградами (№ 1 и № 2)
Материалы и методы исследования
Рассматривается нестационарная задача о течении вязкой несжимаемой жидкости со свободной поверхностью раздела в канале переменного сечения. Течение в лотке считается двумерным, т.е. геометрия лотка имеет бесконечную длину в z-направлении, ось х направлена вдоль лотка, а ось у – вертикально вверх.
Течение жидкости в лотке описывается уравнениями Навье-Стокса (1–3), которые решаются численным методом конечных объемов при использовании модели VOF (Volume of Fluid) [10] совместно с уравнением сохранения скалярной величины ?:
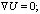 (1)
(1)
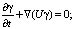 (2)
(2)
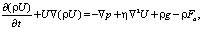 (3)
(3)
где U(x,y,t) – скорость жидкости, p – давление, g = 9,81 м/с2 – ускорение силы тяжести, ? – объемная концентрация несущей жидкости в расчетной ячейке. Значение скалярной функции ? в ячейке может обозначать одно из трех состояний: ? = 0 – ячейка содержит только воздух; ? = 1 – ячейка содержит только воду; 0 < ? < 1 – ячейка содержит границу раздела между жидкостью и газом. Физические свойства среды рассчитываются как средневзвешенные величины в соответствии с объемными концентрациями фаз в каждой ячейке. Средневзвешенная плотность в ячейке рассчитывается как 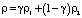 , где ?1 – плотность несущей жидкости, ?2 – плотность воздуха; соответственно вязкость
, где ?1 – плотность несущей жидкости, ?2 – плотность воздуха; соответственно вязкость 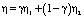 . F? – сила, обусловленная поверхностным натяжением:
. F? – сила, обусловленная поверхностным натяжением: 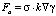 , где ? = 72,8?10-3 Н/м – коэффициент поверхностного натяжения вода-воздух,
, где ? = 72,8?10-3 Н/м – коэффициент поверхностного натяжения вода-воздух, 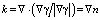 .
.
Граничные условия на жестких стенках канала (и стенках жестких преград) устанавливаются следующими:
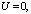
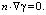 (4)
(4)
Программная реализация численного метода построена на основе свободно распространяемого (http://www.openfoam.org) вычислительного инструментария OpenFOAM.
Оценка точности и достоверности численных результатов проводилась сопоставлением расчетов с экспериментальными данными, полученными в идентичных условиях.
Результаты исследования и их обсуждение
Для регистрации волновых процессов в лотке используются резистивные датчики уровня воды, измерительная аппаратура [7, 8], цифровой осциллограф и двухканальный регистратор Velleman PCS 500. Резистивными датчиками, измерялось смещение свободной поверхности воды в зависимости от времени ?(t). Это позволило построить волновые диаграммы для каждого эксперимента, определить скорости всех волн, а также, при взаимодействии с преградами вычислять энергии волн: падающей W, отраженной WR и прошедшей WT через преграду волн [5].
На рис. 2 дано сравнение экспериментальной осциллограммы высоты волны от времени ?(t), измеренной датчиком уровня на расстоянии 5,245 м от начала лотка, с расчетной зависимостью при идентичных начальных условиях: Н = 0,103 м; A/H = 0,035. Видно, что экспериментальная зависимость очень хорошо согласуется с расчетной.
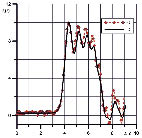
Рис. 2. Зависимость высоты волны от времени ?(t) на расстоянии 5,245 м от начала лотка: (1) – эксперимент, (2) – численный расчет
На рис. 3 приведена зависимость относительной энергии прошедшей волны в процентном отношении от расстояния между преградами, полученная путем численного расчета в данной работе. Численное моделирование проводилось при значениях безразмерных параметров: h/(H + A) ? 0,84 и A/H = 0,035. Расстояния между преградами выражены в виде безразмерного параметра ?/Н. Видно, что относительная энергия прошедшей волны зависит от расстояния между преградами и имеет ярко выраженный минимум в области, соответствующей расстоянию ? = 2Н, при этом энергия прошедшей волны составляет всего 35 % от падающей. При расстоянии ? = 0, т.е. для одиночной преграды, энергия прошедшей волны составляет около 50 % от падающей волны. В работе [9], в которой все результаты приведены в размерных координатах, наиболее выраженный минимум заплеска наблюдался при высоте преград h = 75 мм и расстоянием между ними ? = 200 – 250 мм, при этом: А = 30 мм, Н = 105 мм, а ? = 3 м. Таким образом, условия этих экспериментов соответствуют безразмерным параметрам: A/H = 0,29, h/(H + A) ? 0,55, ?/Н = 0 – 4,57. Так как по высоте заплеска можно судить об энергии прошедшей волны, на рис. 3, для сравнения, приведены величины L(мм) заплесков прошедшей через двойные преграды волны, в зависимости от безразмерного параметра ?/Н. Видно, что эксперименты работы [9] качественно соответствуют нашим расчетным данным – при ?/Н = 2 наблюдается ярко выраженный минимум заплеска.
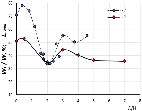
Рис. 3. 1 – обобщенная зависимость высоты заплеска L от расстояния между преградами [9] при значениях безразмерных параметров h/(H + A) ? 0,55, A/H = 0,29; 2 – обобщенная зависимость относительной энергии прошедшей волны от расстояния между преградами при значениях безразмерных параметров h/(H + A) ? 0,84 и A/H = 0,035
Чем же объясняется экспериментально обнаруженный минимум заплеска [9] и минимум энергии прошедшей волны, полученный в результате нашего численного эксперимента?
На рис. 4 приведены поля скоростей вблизи затопленных преград, полученные в результате наших численных расчетов, в моменты времени, когда образовавшиеся вихревые структуры за преградами уже установились.
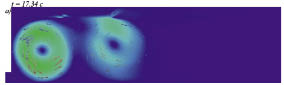

Рис. 4. Визуализация полей скоростей в момент установления вихревых структур вблизи погруженных преград при прохождении через неё гравитационной волны типа цунами при A/H = 0,035: а) для одной преграды; б) для двух преград при ?/Н = 2



