МОДЕЛИРОВАНИЕ АКУСТООПТИЧЕСКОГО ВЗАИМОДЕЙСТВИЯ С ИСПОЛЬЗОВАНИЕМ БОРНОВСКОГО ПРИБЛИЖЕНИЯ
1
Базыкин С.Н. 1 Базыкина Н.А. 1 Кучумов Е.В. 1 Чураков П.П. 1
1 ГОУ ВПО «Пензенский государственный университет»
В статье проведено теоретическое рассмотрение вопросов акустооптического рассеяния света на ультразвуке в акустооптических лазерных интерферометрах информационно-измерительных систем. Определено, что одним из основных элементов информационно-измерительных систем на основе лазерных интерферометров является акустооптический модулятор, в котором происходит взаимодействие оптических и ультразвуковых волн в результате дифракции света на ультразвуке. Показано, что акустооптическое взаимодействие представляет собой процесс рассеяния оптического поля на вариациях оптической неоднородности среды, создаваемой акустическими волнами. В статье делается вывод о том, что моделирование акустооптического рассеяния света на ультразвуке с использованием борновского приближения позволяет решить сложную задачу построения интерференционной картины, которую можно использовать для анализа метрологических характеристик информационно-измерительных систем с использованием лазерных интерферометров.
акустооптическое взаимодействие
акустооптический модулятор
борновское приближение
информационно-измерительная система
интерференционная картина
оптические и акустические волны
1. Базыкин С.Н. Анализ помехоустойчивости информационно-измерительных систем / Базыкин С.Н., Базыкина Н.А. // Фундаментальные исследования. – 2015. – № 3. – С. 19–22.
2. Базыкин С.Н. Принципы построения и состояние производства информационно-измерительных систем линейных перемещений / С.Н. Базыкин, Н.А. Базыкина, Н.П. Кривулин // Современные проблемы науки и образования. – 2015. – № 1; URL: http://www.science-education.ru/121-17219.
3. Ландау Л.Д. Теоретическая физика / Ландау Л.Д., Лифшиц Е.М. // Уч. пособ. для вузов. В 10 т. Т. VI. Гидродинамика. – 5-е изд., стереот. – М.: Физматлит, 2001. – 736 с.
4. Шутилов В.А. Основы физики ультразвука // Учеб. пособ. – Л.: Изд-во Ленингр. ун-та, 1980. – 280 с.
5. Руденко О.В. Теоретические основы нелинейной акустики / Руденко О.В., Солуян С.И. – М.: Наука, 1975. – 287 с.
6. Ландсберг Г.С. Оптика // Учеб. пособие для вузов. – 6-е изд., стереот. – М.: Физматлит, 2003. – 848 с.
7. Сивухин Д.В. Общий курс физики // Уч. пособ. для вузов. В 5 т. Т. IV. Оптика. – 3-е изд., стереот. – М.: Физматлит, 2005. – 792 с.
8. Тихонов А.Н. Уравнения математической физики / Тихонов А.Н., Самарский А.А. // Уч. пособие. – 6-е изд., испр. и доп. – М.: Изд-во МГУ, 1999. – 799 с.
Метрологические требования контроля автоматизированного технологического оборудования имеют тенденцию к увеличению числа параметров контроля, что приводит к созданию измерительных систем, качество которых во многом зависит от точностных характеристик входящих в их состав устройств. К таким системам относятся измерительные системы, в состав которых входят акустооптические лазерные интерферометры, работающие на принципах гетеродинной лазерной интерферометрии [1, 2].
Одним из основных элементов акустооптических лазерных интерферометров является акустооптический модулятор, в котором происходит взаимодействие оптических и ультразвуковых волн в результате дифракции света на ультразвуке.
Акустооптическое взаимодействие представляет собой процесс рассеяния оптического поля на вариациях оптической неоднородности среды, создаваемых акустическими волнами. Акустическое поле, возбуждаемое в пространстве, образует в среде светозвуковода сложное распределение показателя оптического преломления среды.
Рассмотрим распространение акустических колебаний ультразвукового диапазона малой амплитуды в прямоугольном волноводе, заполненном немагнитной диэлектрической жидкостью. Будем отталкиваться от фундаментального уравнения акустики [3]
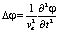 , (1)
, (1)
где 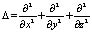 – оператор Лапласа в декартовых координатах; ?(x, t) – потенциал скоростей, т.е.
– оператор Лапласа в декартовых координатах; ?(x, t) – потенциал скоростей, т.е. 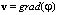 или
или 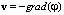 ;
; 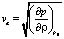 , ?0 – равновесная плотность жидкости. Связь изменения локальной плотности жидкости с потенциалом скорости ? выразится следующим образом [4]:
, ?0 – равновесная плотность жидкости. Связь изменения локальной плотности жидкости с потенциалом скорости ? выразится следующим образом [4]:
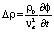 . (2)
. (2)
В одном из торцов волновода расположен источник ультразвуковых волн, противоположный торец устроен так, чтобы не создавать отражённых волн в объёме волновода. Начало координат совпадает с центром излучателя, ось Ox совпадает с осью волновода, оси Oy и Oz перпендикулярны стенкам волновода, а в местах с координатами 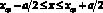 ,
, 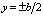 имеются оптически-прозрачные окна (рис. 1).
имеются оптически-прозрачные окна (рис. 1).
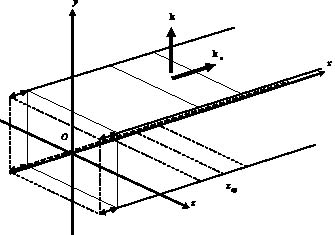
Рис. 1. Схема распространения акустических колебаний в прямоугольном волноводе
Излучатель представляет собой пьезокварцевую пластинку, колеблющуюся по толщине. В этом случае излучатель будет генерировать плоские акустические волны, распространяющиеся вдоль оси Ox [3, 4]:
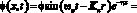
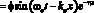 , (3)
, (3)
где ?a – частота колебаний излучателя, Ka = (ka, 0, 0) – волновой вектор, 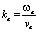 – волновое число, ? – коэффициент поглощения ультразвуковой волны в результате вязких потерь.
– волновое число, ? – коэффициент поглощения ультразвуковой волны в результате вязких потерь.
Акустические волны распространяются вдоль волновода без искажения в соответствии с законами геометрической акустики, так как имеют малую длину волны и сохраняют плоскую волну при распространении в волноводе [4]. Таким образом, вследствие малой амплитуды, можно пренебречь такими эффектами, как акустическое течение, деформация волнового фронта около стенок волновода и т.п. [4, 5].
Подставляя (3) в (2), получаем выражение для изменений локальной плотности среды:
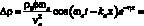
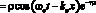 .
.
Плотность среды ? определяется выражением
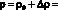
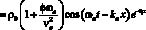 . (4)
. (4)
Рассмотрим связь плотности жидкости ? с её абсолютным показателем преломления n. Известно [6, 7], что связь показателя преломления с микроскопическими характеристиками среды выражается следующим образом:
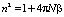 , (5)
, (5)
где N – число молекул в единице объёма; ? – поляризуемость молекул среды.
Учитывая, что N = ?/?, где ? – молярная масса вещества, выражение (5) можно переписать в следующем виде:
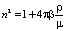 . (6)
. (6)
Уравнения изменения напряженности световой электромагнитной волны для вектора напряженности электрического поля через оптически неоднородную среду определяется выражением [6, 7]:
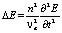 . (7)
. (7)
Так как среда представляет собой жидкость немагнитную и диэлектрическую (поляризация волны не играет роли), можно описать ее с помощью вектора одной из её проекций E(x, y, z, t) [6, 7, 8]. С учётом данного замечания и выражений (4) и (6), уравнение (7) перепишется в виде
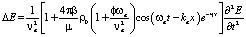
или
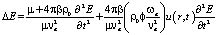 , (8)
, (8)
где
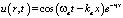 .
.
Так как значения оптических частот намного больше акустических 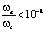 , то можно воспользоваться так называемым бриллюэновским квазистатическим приближением и считать, что u(r, t) ? u(r) (рис. 2), предполагая акустическую волну неподвижной в процессе рассеяния, а ?at в выражении
, то можно воспользоваться так называемым бриллюэновским квазистатическим приближением и считать, что u(r, t) ? u(r) (рис. 2), предполагая акустическую волну неподвижной в процессе рассеяния, а ?at в выражении 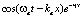 рассматривать как параметр.
рассматривать как параметр.
Представив решение уравнения (8) в виде 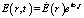 , приходим к следующему уравнению:
, приходим к следующему уравнению:
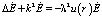 , (9)
, (9)
где 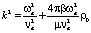 ,
, 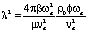 .
.
Используя функцию Грина, с учетом 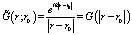 и уравнения (8), переходим от уравнения (9) к интегральному уравнению
и уравнения (8), переходим от уравнения (9) к интегральному уравнению
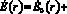
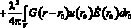 , (10)
, (10)
где 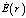 представляет собой решение уравнения (9) для ? = 0 и удовлетворяющее соответствующим граничным условиям.
представляет собой решение уравнения (9) для ? = 0 и удовлетворяющее соответствующим граничным условиям.
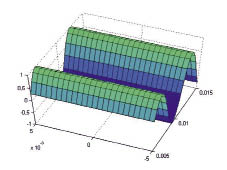
Рис. 2. Функция 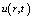 для t = 0
для t = 0
Трехмерное сингулярное интегральное уравнение имеет вид:
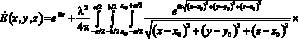
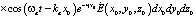 . (11)
. (11)
Вследствие малого значения амплитуды акустической волны, т.е. при малом значении второго слагаемого уравнения (8), напряжённость E на выходе из области взаимодействия с акустическим полем можно представить в виде
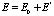 , (12)
, (12)
где E0 – невозмущённая составляющая напряженности световой волны, E’ – рассеянная составляющая, 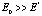 .
.
Подставляем (12) в (8). После отбрасывания членов порядка выше первого получаем следующее неоднородное уравнение:
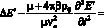
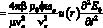 . (13)
. (13)
Рассмотрим наиболее важный практический случай, когда падающая и рассеянная волны монохроматичны, то есть:
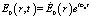 ,
,
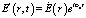 . (14)
. (14)
Точка над функцией означает умножение на ei?t. Подставляя (14) в (13) и сокращая множитель 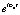 , окончательно приходим к неоднородному уравнению Гельмгольца:
, окончательно приходим к неоднородному уравнению Гельмгольца:
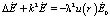 . (15)
. (15)
В первом борновском приближении теории возмущений [8] решение уравнения (15) можно представить в виде
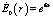 ,
, 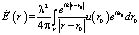 .
.
Наиболее интересным является случай, когда V – объём в виде прямоугольного параллелепипеда 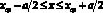 ;
; 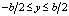 ;
; 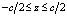 со сторонами a, b и c (a ? b ? с) и k = (0, k, 0) – плоская волна. Тогда:
со сторонами a, b и c (a ? b ? с) и k = (0, k, 0) – плоская волна. Тогда:
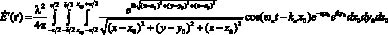 . (16)
. (16)
К сожалению, факторизовать ядро в выражении (16) в декартовых координатах невозможно. Это не позволяет получить аналитическое выражение или хотя бы упростить данный интеграл. Поэтому целесообразно рассматривать интерференционную картину на плоскости 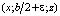 , ? > 0, оставаясь в области, где интеграл (16) не является сингулярным.
, ? > 0, оставаясь в области, где интеграл (16) не является сингулярным.
При описании интерференции интенсивность света определяют по усреднённому по времени квадрату напряженности [6, 7]:
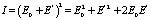 . (17)
. (17)
Для случая монохроматических волн уравнение (17) будет иметь вид
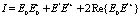 , (18)
, (18)
где * означает комплексное сопряжение.
На рис. 3 представлена интерференционная картина, рассчитанная по предложенной методике, для следующих значений параметров: t = 0 сек, a = b = c 10–2 м, xcp 10–2 м, ? = 5?10–2, ? = 1,5?10–30 м3, ?0 = 103 кг/м3, ? = 18 а.е.м. = 3?10–26 кг, va = 1,4?103 м/с, ?a = 6? ?106 рад/с, vc = 3?108 м/с, ?c = 1015 рад/с, k = 4,3? ?106 рад/м, ? = 2,4?103 рад/м, ka = 103 рад/м, ? = 0,5 м-1.
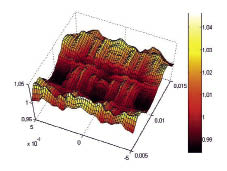
Рис. 3. Интерференционная картина акустооптического взаимодействия
Применим к уравнению (20) метод разделения переменных (метод Фурье) и представим решение уравнения в факторизованном виде [6]:
После подстановки (21) в (20), получаем систему обыкновенных дифференциальных уравнений со следующими граничными условиями:
Условия (24) для уравнения (23) подразу мевают, что стенки у волновода на рис. 1 сделаны из светоотражающего материала, за исключением оптически-прозрачных окон. Решение (23) с граничными условиями (24) имеет вид
Таким образом, в описании акустооптического взаимодействия возможно применение борновского приближения. Однако стоит отметить, что даже при вычислении интеграла (16) приходится использовать нестандартные подходы, т.к. интегрируемая часть является сильноосциллирующей функцией и данный вопрос требует отдельного рассмотрения.
Моделирование акустооптического взаимодействия с использованием борновского приближения позволяет решить достаточно сложную задачу построения интерференционной картины, которую можно использовать для анализа метрологических характеристик информационно-измерительных систем с использованием лазерных интерферометров.
Базыкин С.Н., Базыкина Н.А., Кучумов Е.В., Чураков П.П. МОДЕЛИРОВАНИЕ АКУСТООПТИЧЕСКОГО ВЗАИМОДЕЙСТВИЯ С ИСПОЛЬЗОВАНИЕМ БОРНОВСКОГО ПРИБЛИЖЕНИЯ // Современные наукоемкие технологии. 2015. № 12-1.
С. 9-13;
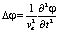 , (1)
, (1)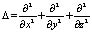 – оператор Лапласа в декартовых координатах; ?(x, t) – потенциал скоростей, т.е.
– оператор Лапласа в декартовых координатах; ?(x, t) – потенциал скоростей, т.е. 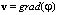 или
или 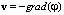 ;
; 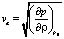 , ?0 – равновесная плотность жидкости. Связь изменения локальной плотности жидкости с потенциалом скорости ? выразится следующим образом [4]:
, ?0 – равновесная плотность жидкости. Связь изменения локальной плотности жидкости с потенциалом скорости ? выразится следующим образом [4]: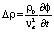 . (2)
. (2)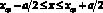 ,
, 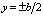 имеются оптически-прозрачные окна (рис. 1).
имеются оптически-прозрачные окна (рис. 1).




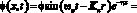
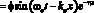 , (3)
, (3)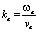 – волновое число, ? – коэффициент поглощения ультразвуковой волны в результате вязких потерь.
– волновое число, ? – коэффициент поглощения ультразвуковой волны в результате вязких потерь.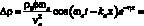
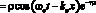 .
.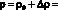
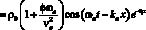 . (4)
. (4)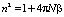 , (5)
, (5)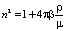 . (6)
. (6)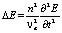 . (7)
. (7)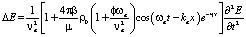
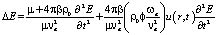 , (8)
, (8)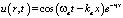 .
.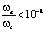 , то можно воспользоваться так называемым бриллюэновским квазистатическим приближением и считать, что u(r, t) ? u(r) (рис. 2), предполагая акустическую волну неподвижной в процессе рассеяния, а ?at в выражении
, то можно воспользоваться так называемым бриллюэновским квазистатическим приближением и считать, что u(r, t) ? u(r) (рис. 2), предполагая акустическую волну неподвижной в процессе рассеяния, а ?at в выражении 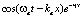 рассматривать как параметр.
рассматривать как параметр.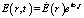 , приходим к следующему уравнению:
, приходим к следующему уравнению: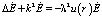 , (9)
, (9)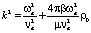 ,
, 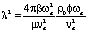 .
.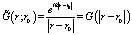 и уравнения (8), переходим от уравнения (9) к интегральному уравнению
и уравнения (8), переходим от уравнения (9) к интегральному уравнению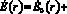
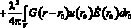 , (10)
, (10)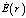 представляет собой решение уравнения (9) для ? = 0 и удовлетворяющее соответствующим граничным условиям.
представляет собой решение уравнения (9) для ? = 0 и удовлетворяющее соответствующим граничным условиям.
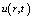 для t = 0
для t = 0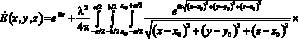
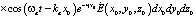 . (11)
. (11)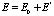 , (12)
, (12)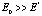 .
.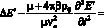
 . (13)
. (13)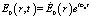 ,
, 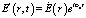 . (14)
. (14)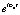 , окончательно приходим к неоднородному уравнению Гельмгольца:
, окончательно приходим к неоднородному уравнению Гельмгольца: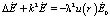 . (15)
. (15)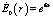 ,
, 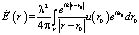 .
.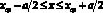 ;
; 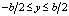 ;
; 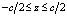 со сторонами a, b и c (a ? b ? с) и k = (0, k, 0) – плоская волна. Тогда:
со сторонами a, b и c (a ? b ? с) и k = (0, k, 0) – плоская волна. Тогда: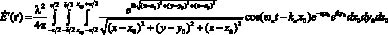 . (16)
. (16)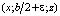 , ? > 0, оставаясь в области, где интеграл (16) не является сингулярным.
, ? > 0, оставаясь в области, где интеграл (16) не является сингулярным.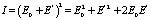 . (17)
. (17)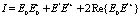 , (18)
, (18)
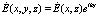 . (19)
. (19)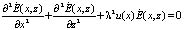 . (20)
. (20)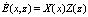 . (21)
. (21)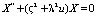 , (22)
, (22)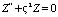 , (23)
, (23)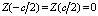 . (24)
. (24)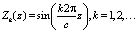 .
.