Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Тувин А.А. 1

---

1 ФГБОУ ВО «Ивановский государственный политехнический университет»

Технологический процесс ткачества сетки, учитывая специфические свойства металлонитей, оказывается особенно чувствительным к деформационным свойствам звеньев механизмов, к колебательным процессам в исполнительных механизмах станка. Деформационные и колебательные процессы можно минимизировать на стадии проектирования или модернизации ткацкого оборудования. Решение данных задач можно получить при наличии динамических и математических моделей, учитывающих взаимосвязи между технологическими объектами (нити основы и утка) и исполнительными механизмами. В частности, необходим учет взаимодействия батанного и рапирного механизмов с упругой системой заправки станка, через которую раскрываются согласующие связи работы основных исполнительных механизмов. Разработана математическая модель анализа собственных частот и форм изгибно-крутильных колебаний бруса широких металлоткацких станков с n лопастями, соответствующая его уточненной динамической модели. Установлено, что на вибрационные процессы в батанных механизмах металлоткацких станков типа СТР влияют изгибная жесткость бруса и его погонная масса, в связи с этим при проектировании или модернизации батанных механизмов нужно стремиться к увеличению изгибной жесткости бруса и снижению его погонной массы.

Статья в формате PDF

961 KB

ткацкий станок

батан

брус

опушка ткани

частота колебаний

амплитуда

1. Беляев, Н.М. Сопротивление материалов. – 15-е изд. перераб. – М.: Главная редакция физико-математической литературы изд-ва «Наука». – 1976. – С. 608.

2. Мельяченко Ж.В. Взаимосвязь технологических параметров ткачества и параметров строения вырабатываемых тканей / Ж.В. Мельяченко, С.Д. Николаев // Изв. вузов. Технология текстильной промышленности. – 1991. – № 1. – С. 47–50.

3. Мигушов И.И. Механика текстильной нити и ткани. – М.: Легкая индустрия, 1980. – 160 с.

4. Смирнов В.И. Курс высшей математики: учебное пособие для втузов: В 6-ти т. Т.1. – М.: Наука, 1965. – 480 с.

5. Суров В.А. Динамика упругих систем батанных механизмов металлоткацких станков / В.А. Суров, А.А. Тувин. – Иваново: ИГТА, 2004. – 188 с.

6. Суров В.А. Исследование батанного механизма металлоткацких станков типа СТР с выстоем в момент прибоя / В.А. Суров, А.А. Тувин, А.В. Ковалевский, В.Г. Чумиков // Изв. вузов. Технология текстильной промышленности. – 1996. – № 3. – С. 90–93.

7. Тимошенко С.П. Колебания в инженерном деле. – М.: Наука, 1967. – 444 с.

Серийно выпускаемые металлоткацкие станки имеют цикловую диаграмму работы кулачкового привода батана типа «выстой – подъем – опускание – выстой» [5, 6]. Этот цикл можно представить состоящим из нескольких фаз: первая фаза – движение батана до зоны формирования сетки (движение батана до момента касания берда с опушкой вырабатываемой сетки); вторая фаза – движение батана в процессе формирования сетки; третья фаза – отход батана от зоны формирования и четвертая фаза – выстой. Поставленная цель требует первоначально решения задачи динамики бруса в первой и второй фазах его движения, т.к. в других фазах колебания бруса батана не влияет на процесс формирования сетки.

В первой фазе движения на брус действуют только инерционные нагрузки. Тем не менее вызываемые ими колебательные процессы приводят к тому, что при подходе к зоне формирования сетки брус теряет первоначальную прямолинейную форму, деформируясь в плоскости касательной к поверхности движения. Кроме того различные сечения бруса будут иметь в этот момент и различные скорости. То есть вторая фаза движения батана, на которой к брусу дополнительно прикладывается сопротивление со стороны опушки вырабатываемой сетки, имеет конкретные начальные условия. Известно [7], что при этом в системе будут возникать свободные, свободные-сопровождающие и вынужденные колебания. А поскольку плоскость действия сил технологического сопротивления не является плоскостью расположения линии центров изгиба бруса, то это будут изгибно-крутильные колебания. С точки зрения механики интерес представляют возникающие при этом в системе силы и напряжения. С точки зрения технологии – форма берда (форма линии берда, соприкасающейся с опушкой) в момент отхода его от опушки вырабатываемой сетки.

Брус – равного сечения, поэтому в динамической модели представим его в виде стержня с равномерно распределенной массой интенсивностью m. Если через mв обозначим массу бруса в сборе с бердом, то 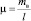(рис. 1).

Рис. 1. Динамическая модель бруса батана станка с n – лопастями

Изгибом бруса в плоскости ZOX аналогично [2] будем пренебрегать ввиду его малости. Действующие в этой плоскости инерционные силы существенно ниже инерционных сил и сил технологического сопротивления, действующих в плоскости XOY. При изгибе бруса в плоскости XOY лопасти будут испытывать деформацию кручения, а подбатанный вал будет подвергаться изгибу. Причем на прогиб подбатанного вала под действием моментов со стороны лопастей оказывает влияние не только жесткость самого вала, но и радиальная податливость его подшипниковых опор. Податливость этой системы в динамической модели отражается упругой связью с коэффициентом жесткости с₂ – приведенной к лежащей в плоскости изгиба оси бруса крутильной жесткостью системы лопасть – подбатанный вал – подшипники подбатанного вала, с₃ – приведенный к крутильной коэффициент жесткости лопасти. Лопасти обладают инерционными свойствами, которые моделируются сосредоточенными массами m – приведенными к концевым сечениям бруса массами лопасти в сборе с подбатанным валом.

Податливости подшипниковых соединений брус – шатун, шатун – коромысло, главный вал – станина отражаются упругой связью с коэффициентом жесткости c₁ – приведенной к концевым сечениям бруса жесткостью указанных подшипниковых соединений.

Упругое сопротивление системы заправки на фазе формирования сетки моделируется коэффициентом kn постели [3]. Кроме того, поскольку сопротивление со стороны опушки вырабатываемой сетки действует не в плоскости изгиба бруса, на брус будет действовать распределенный крутящий момент, интенсивностью Mk. Кроме силового возмущения брус испытывает кинематическое возмущение – по определяемому профилем кулачков закону 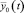перемещаются точки крепления упругих связей c₁. Массами шатунов и коромысел при этом по малости будем пренебрегать. Методика определения коэффициента постели kп, модуль или жесткость упругого основания – коэффициент пропорциональности между интенсивностью q(x) реакции упругого основания (реакции, приходящейся на единицу длины основания), и прогибом y(x) основания в рассматриваемом сечении, коэффициентов С₁, С₂ и С₃ изложена в [5].

Обозначим через EI_z жесткость поперечного сечения бруса батана при изгибе. Здесь E – модуль упругости первого рода материала бруса; I_z – момент инерции площади поперечного сечения бруса относительно нейтральной оси [1]. Жесткость бруса на кручение обозначим через GI_к, где G – модуль сдвига материала бруса; I_к – момент инерции при кручении. При расчете жесткости лопасти следует иметь в виду, что она имеет переменное сечение. Поскольку угол dφ закручивания элемента dz лопасти под действием момента M_σ со стороны бруса равен 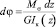, то приведенная жесткость 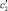лопасти определится выражением

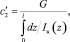(1)

где l – длина скручиваемого участка лопасти.

Рассмотрим схему станка СТР-130-М и представим подбатанный вал в виде четырехопорной статически неопределимой балки, нагруженной сосредоточенными моментами, возникающими от кручения лопастей батана (рис. 1). Приведенный коэффициент жесткости c₂ системы лопасть – подбатанный вал – подшипники подбатанного вала будет равен [5]

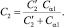(2)

Уравнение движения бруса на различных фазах его движения получим, применяя вариационный принцип Гамильтона – Остроградского [7]. Интеграл действия (интеграл Гамильтона) согласно [7] для системы с распределенными параметрами можно представить в виде

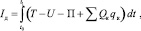
где T – кинетическая энергия; U – потенциальная энергия упругой системы; П – потенция внешних сил; Q_к – обобщенные неконсервативные силы; q_к – обобщенные координаты. Принцип Гамильтона – Остроградского имеет форму δI_д = 0.

Как отмечалось, в общем случае брус батана подвержен изгибу в плоскости X0Y и кручению. На брус действуют:

– инерционное (кинематическое) возмущение интенсивностью

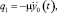
где y₀(t) – кинематическое перемещение точек крепления упругих связей c₁ на рассматриваемой фазе движения;

– внутреннее неупругое сопротивление [7] интенсивностью

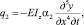
где α₂ – модуль вязкости;

– внешнее неупругое сопротивление

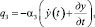
где y(x, t) – прогиб сечений бруса; α₃ – коэффициент пропорциональности;

– внутреннее неупругое сопротивление

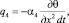
где θ(x, t) – угол поворота сечений бруса при кручении; α₄ – коэффициент пропорциональности;

– внешнее неупругое сопротивление

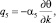
где α₅ – коэффициент пропорциональности;

– сила сопротивления со стороны упругой системы заправки станка (УСЗ)

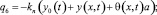
– момент сопротивления со стороны УСЗ

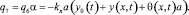
Вид выражений для кинетической и потенциальной энергий системы зависит от принимаемой теории. При анализе крутильных колебаний в данном случае применима техническая теория. При анализе поперечных колебаний мы будем опираться на уточненную теорию изгибных колебаний стержней – теорию С.П. Тимошенко [7]. В нашем случае, согласно [7], поправки, учитывающие влияние инерции поворотов и сдвигов, могут иметь большое значение. Тогда пренебрегая для данного сечения бруса смещением линии центров изгиба относительно центральной оси, будем иметь следующие выражения для кинетической и потенциальной энергий бруса батана:

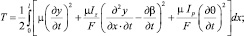
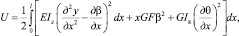
где F – площадь поперечного сечения бруса; I_p – полярный момент инерции площади поперечного сечения относительно центра масс; β – средний угол сдвига; x – численный коэффициент, зависящий от формы поперечного сечения.

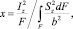
где 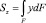– статический момент относительно нейтральной оси Z части поперечного сечения, отсеченного плоскостью y = const; b – ширина поперечного сечения на уровне y = const.

Интеграл действия в общем случае принимает вид

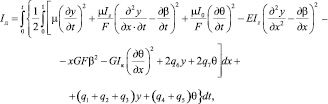
то есть

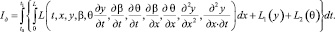
Уравнения Эйлера ‒ Пуассона [4] примут вид

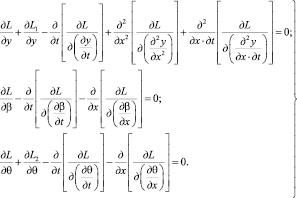(3)

Имея результаты частотного анализа изгибных и крутильных колебаний бруса на второй фазе движения батана [3], можно оценить и влияние связанности этих колебаний. При этом мы не будем учитывать возникающую при кручении депланацию поперечного сечения бруса. Если пренебречь силами неупругого сопротивления, то на основании уравнений (3) уравнения, описывающие собственные изгибно-крутильные колебания бруса на второй фазе движения батана, будут иметь вид

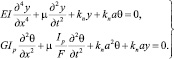(4)

Принимая решение в виде 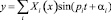и 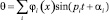, для балки, рис. 1, получим

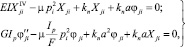(5)

где j – номер участка балки (от 1 до n – 1).

Решение уравнений форм (5) для каждого j-го участка ищется в виде

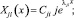
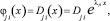(6)

где C_ji, D_ji – постоянные коэффициенты форм.

Подставляя (6) в (5), будем иметь

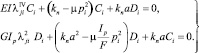(7)

Для получения частотного уравнения системы (7) воспользуемся граничными условиями участков балки:

при изгибе

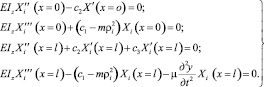(8)

при кручении

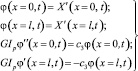(9)

и условиями сопряжения участков:

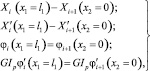(10)

при этом согласно первому уравнению системы (5) имеем

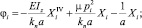
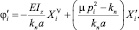
Таким образом, получено 12 уравнений, соответствующие граничным условиям и условиям сопряжения участков бруса батана, которые можно представить в виде следующей системы:

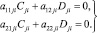
В результате решения данной системы уравнений с помощью формул Крамера [4] получаем коэффициенты форм C_ji, D_ji.

С использованием разработанной методики расчета собственных изгибно-крутильных колебаний применительно к станку СТР-100-М были получены результаты, аналогичные приведенным в работе [5]. Первые три формы собственных изгибно-крутильных колебаний бруса батана станка СТР-100-М приведены на рис. 2.

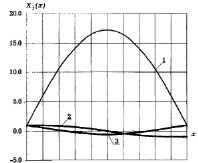
Рис. 2. Первые три формы собственных изгибно-крутильных колебаний бруса батана металлоткацкого станка СТР-100-М

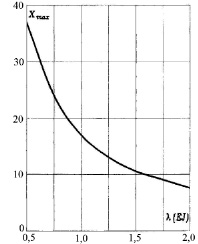
Рис. 3. Влияние жесткости бруса на амплитуду первой формы изгибно-крутильных колебаний бруса батана металлоткацкого станка СТР-100-М

Как следует из рис. 2, максимальное отношение между амплитудами колебаний различных сечений бруса при реализации первой формы. Максимальный прогиб при этом будет иметь место в сечении x = l/2. Относительные амплитуды колебаний при второй и третьей формах имеют небольшие значения. При этом нужно отметить, что высокочастотные колебания затухают значительно быстрее, т.е. в первую очередь при анализе динамики батанного механизма нужно обращать внимание на колебания, соответствующие первой гармонике. Влияние жесткости бруса батана на максимальные значения относительной амплитуды при реализации первой формы колебаний приведено на рис. 3. Ввиду незначительности (< 1) данной зависимости по второй и третьей формам они не показаны, а по первой форме видно значительное снижение амплитуды колебаний при увеличении жесткости бруса батана.

Необходимо отметить, что хотя абсолютные значения амплитуд колебаний сечений бруса батана определяются анализом вынужденных колебаний, однако и анализ собственных изгибно-крутильных колебаний показывает, что при проектировании (или модернизации) бруса батанного механизма металлоткацких станков необходимо стремиться к реализации возможностей увеличения первой собственной частоты колебаний, тем самым – к увеличению изгибной собственности бруса.

Выводы

1. Разработана математическая модель собственных частот и форм изгибно-крутильных колебаний бруса широких металлоткацких станков с n лопастями, соответствующая его уточненной динамической модели бруса на фазе взаимодействия берда с опушкой вырабатываемой сетки.

2. Установлено, что на вибрационные процессы в батанных механизмах металлоткацких станков типа СТР влияют изгибная жесткость бруса и его погонная масса, в связи с этим при проектировании или модернизации батанных механизмов нужно стремиться к увеличению изгибной жесткости бруса и снижению его погонной массы.

Библиографическая ссылка