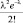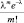Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Сафронова Т.И. 1 Самурганов Е.Е. 1 Степанов В.И. 2

---

1 ФГБОУ ВПО «Кубанский государственный аграрный университет»

2 Алтайский экономико-юридический институт

Развитие сельского хозяйства и промышленности должно основываться на освоении новых методов управления и внедрения новейших технологий и использовании эффективных методов научных исследований. К таким эффективным методам следует отнести математизацию исследований. Прогресс в области вычислительной техники создал базу для перехода от описательного подхода к использованию количественных методов, основанных на использовании математических процедур и соответствующих моделей. Математическая модель – мощное средство обобщения разнородных данных об объекте, позволяющее осуществить прогнозирование будущего поведения объекта. В статье приведены задачи прикладного характера, которые показывают применение теории вероятностей в практической деятельности выпускника вуза.

Статья в формате PDF

746 KB

высшее образование

случайные величины

математическая модель

вероятностный расчет

1. Кузнецов Е.В., Хаджиди А.Е. Сельскохозяйственный мелиоративный комплекс для устойчивого развития агроландшафтов: монография. – Краснодар: Изд-во «ЭДВИ», 2014. – 199 с.

2. Сафронова Т.И. Математическая модель экологической ситуации на рисовой оросительной системе / Т.И. Сафронова, Л.М.Рекс, Умывакин В.М., Приходько И.А. // Научный журнал КубГАУ. – 2008. – № 44(10). – 17 с. http://ej.kubagro.ru

3. Сафронова Т.И. Математическая модель экологической ситуации на рисовых оросительных системах // Известия вузов. Северо-Кавказский регион, технические науки, приложение № 1. – Новочеркасск, 2005. – С. 137–140.

4. Сафронова Т.И., Кузнецов Е.В. Системно-информационная оценка экологического состояния рисовой оросительной системы // Мелиорация и водное хозяйство. – 2005. – № 3. – С. 28–30.

5. Сафронова Т.И., Степанов В.И. Математическое моделирование в задачах агрофизики. – Краснодар: КубГАУ, 2012. – 183 с.

В настоящее время высшее образование должно способствовать формированию специалистов широкого профиля, сочетающих глубокие фундаментальные знания и обстоятельную практическую подготовку конкретной отрасли производства.

Практика обучения студентов показывает, что, даже владея достаточным объемом математических сведений, многие студенты затрудняются использовать известные знания. Одной из причин следует назвать недостаточную ориентированность на использование дисциплин других циклов. Следует отметить, что в рабочих программах курса математики часто отсутствует профильный подход.

Важно правильно сочетать фундаментальность с профессионально-прикладной направленностью. В курсе математики нужно формулировать прикладные задачи с четким выявлением их математической сущности. Необходимо научить студентов математически моделировать прикладную ситуацию, отбрасывая все несущественные стороны рассматриваемого процесса. В рамках прикладной направленности для каждой специальности важно разработать свою программу с примерами из данной специальности. Такие примеры оживляют учебный процесс и вызывают интерес к углубленному изучению математики.

Развитие сельского хозяйства и промышленности должно основываться на освоении новых методов управления и внедрения новейших технологий и использовании эффективных методов научных исследований. К таким эффективным методам следует отнести математизацию исследований.

Математизация исследований предполагает в первую очередь получение математической модели исследуемого процесса, достаточно точно, адекватно его описывающей. При наличии такой модели возникает возможность дальнейшее исследование процесса заменить анализом его математической модели для получения решения поставленных конкретных задач.

На заключительном этапе исследования формируется математическая модель исследованных явлений во взаимосвязи с факторами внешней среды. Составленная модель дает возможность научно обоснованно управлять этими явлениями с учетом всех тех взаимосвязей, которые изучили экспериментаторы на предыдущих этапах.

В статье приведем задачи прикладного характера, которые показывают применение теории вероятностей в будущей практической деятельности инженера.

Пример 1. Рассмотрим случайную величину Х, возможные значения которой – целые неотрицательные числа 0, 1, 2, …, m, …, причем последовательность этих значений теоретически не ограничена [1].

Случайная величина Х распределена по закону Пуассона, если вероятность того, что она примет отдельное значение m, выражается формулой

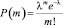(m = 0, 1, 2, …), (1)

где λ = np – параметр закона Пуассона.

Ряд распределения случайной величины Х имеет вид

Числовые характеристики случайной величины, распределенной по закону Пуассона, таковы:

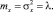(2)

Это единственное распределение, у которого математическое ожидание и дисперсия равны между собой и равны параметру распределения λ.

Примерами случайных величин, подчиняющихся закону распределения Пуассона, могут служить: число обрывов нити определенного сорта пряжи в течение времени Т; число дефектов в куске ткани определенной длины.

Отметим условия, при которых возникает пуассоновское распределение.

Прежде всего, оно является предельным для биномиального, когда число опытов n неограниченно увеличивается (n → ∞) и одновременно вероятность «успеха» в одном опыте неограниченно уменьшается (p → 0), но так, что их произведение np сохраняется в пределе постоянным. Известно, что математическое ожидание случайной величины Х, распределенной по биномиальному закону с параметрами n и р, равно np. В распределении Пуассона обозначено np = λ; из предельного свойства этого распределения с параметром λ = np следует, что его можно приближенно применять вместо биномиального, когда число опытов n очень велико, а вероятность р очень мала, т.е. в каждом отдельном опыте событие А появляется крайне редко.

Помимо этого предельного случая возникновения пуассоновского распределения на практике встречается ряд ситуаций, где это распределение имеет место. В теории надежности параметр λ означает интенсивность потока событий – среднее число появлений события в единицу времени. Значит, если известна продолжительность t испытаний и интенсивность λ, то λt – это среднее число появлений события за время t. В этом случае вероятность того, что за это время событие А появится ровно m раз, вычисляется по формуле

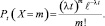(3)

Распределение случайной величины Х, определяемое формулами (1) и (3), называется пуассоновским.

Формула (3) определяет математическую модель простейшего потока событий.

Например, поступление вызовов на станцию «Скорой помощи», моменты прибытия судов в порты.

Интенсивностью потока λ называется среднее число событий, которые появляются в единицу времени.

Тогда, если постоянная интенсивности потока известна, вероятность появления m событий простейшего потока за время t определяется по формуле Пуассона (3):

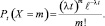
Таким образом, поток событий – еще один тип условий, в которых возникает распределение Пуассона. Тогда указывается среднее число λ появления данного события в некоторой области и размеры S самой области. События в области задания должны быть распределены равномерно и поодиночке и положение каждого из них случайно.

Распределение Пуассона играет важную роль в системе массового обслуживания, когда предполагается, что существует некоторый пуассоновский поток требований с интенсивностью λ (например, среднее число людей, подходящих к кассе магазина за единицу времени). Как систему массового обслуживания можно трактовать фильтрацию влаги в почве, где функцию «касс» выполняют поры, «очередей» – поверхностный сток, возникающий в тех случаях, когда подавляющее большинство пор заполнено водой, а вода продолжает поступать с осадками. Разложение опада в лесу также можно рассматривать как систему массового обслуживания, где в качестве «кассиров» выступают почвенные беспозвоночные и микроорганизмы. Подстилку на поверхности почвы и гумус можно трактовать как «очередь» в системе обслуживания. С этих позиций развитие болота или чернозема можно рассматривать как результат формирования бесконечной очереди.

Пример 2. На балку действует случайная сила Q с известными характеристиками M_Q и D_Q (рис. 1). Требуется определить математические ожидания и дисперсии реакций прогиба в точке приложения силы Q и максимального нормального напряжения. Жесткость балки на изгиб E_Ix.

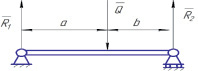
Рис. 1. Шарнирно-опертая балка: Q – активная сила, R₁ и R₂ – реакции опор

Решение

Найдем реакции, прогиб в точке приложения силы Q и максимальное нормальное напряжение в сечении по формулам для детерминированных сил

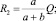
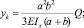
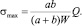
Запишем вероятностные характеристики R₁, R₂, y_k, σ_max

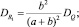
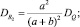
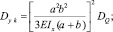
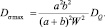
Расчет закончен.

Пример 3. Произвести расчет шарнирно-опертой балки, находящейся под действием случайной нагрузки Р, распределенной по нормальному закону (рис. 2).

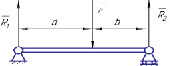
Рис. 2. Шарнирно-опертая балка: Р – активная сила; R₁ и R₂ – реакции опор

а) Детерминированный расчет

1. Находим опорные реакции

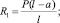
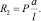
2. Находим максимальный изгибающий момент. Для рассматриваемой балки такой момент находится под силой Р:

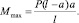
3. Находим максимальное нормальное напряжение

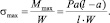
4. Находим допустимый момент сопротивления W из условия прочности

σ_max ≤ σ₀,

где σ₀ – допустимое напряжение на прочность.

Для рассматриваемой балки

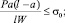
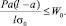
Обычно принимается наименьшее значение W, т.е.

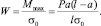
По этому значению W подбирается поперечное сечение балки. Расчет балки закончен.

б) Вероятностный расчет

Целью этого расчета также является получение W для поперечного сечения балки.

Пусть сила Р – случайная величина (СВ) со следующими характеристиками:

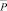– математическое ожидание МО;

P_σ – среднее квадратическое отклонение СКО.

Для определения W условие σ_max ≤ σ₀ заменяется следующим:

P(σ_max ≤ σ₀) = p₀.

Это означает, что неравенство осуществляется с заданной вероятностью p₀, причем p₀ задается в зависимости от степени ответственности балки.

σ_max находится по формуле

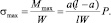
Так как случайная величина Р распределена по нормальному закону, то σmax также будет распределена по нормальному закону со следующими характеристиками:

.

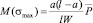Получили уравнение для определения W:

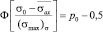
или

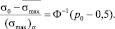
Итак, задаваясь вероятностью p₀ по таблице интеграла вероятностей, найдем значение 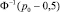. Получаем выражение для определения W.

Рассмотрим численный пример. Пусть a = 50 см, l = 150 см, σ0 = 2100 кг/см²;

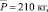P_σ = 30 кг, p₀ = 0,95.

Подготовим выражения для :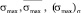

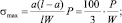
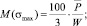
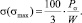
По таблице интеграла вероятностей найдем

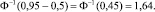
Далее

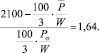
Отсюда W = 4,1 см³.

Таким образом, если принять что неравенство σmax < σ₀ осуществляется с вероятностью p₀ = 0,95, то момент сопротивления поперечного сечения балки следует брать равным 4,1 см³.

Теперь отметим, что, так как случайная величина Р распределена по нормальному закону, согласно правилу трех сигм ее максимальное значение будет 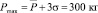. Если провести детерминированный расчет на эту нагрузку, равную 300 кг, то получим W = 4,7 см³.

Полученный результат подчеркивает экономическую целесообразность учета случайности нагрузки.

Выводы

Содержание математического образования с примерами прикладного характера способствует формированию математической культуры и математической компетентности студентов, привлекает студентов к выполнению научно-исследовательских работ и участию в научных конференциях, конкурсах, олимпиадах и выставках.

Библиографическая ссылка