Ряд исследований [1, 4], проведенных в последние годы на шахтах и рудниках различных стран, указывают на влияние взаимной ориентации главных горизонтальных напряжений и горных выработок, что часто является одним из главных факторов, определяющих устойчивость выработок.
Установлено, что выработки, расположенные параллельно оси север-юг, более устойчивы, чем выработки, расположенные перпендикулярно им. Значения максимальных главных напряжений в 2–3 раза больше при перпендикулярном расположении [2, 5], чем при параллельном расположении.
В Карагандинском угольном бассейне с целью изучения влияния направления заложения выработок относительно направления максимальных горизонтальных напряжений на шахтах были проведены наблюдения в 55 выработках на предмет их дефектности. Выработки были разбиты на проведенные параллельно направлению максимальных горизонтальных напряжений (север-юг) и перпендикулярно им.
Анализ результатов производился с учетом следующих факторов [3]:
– расположение выработки: в целике, в присечку, в зоне влияния очистных работ, вне ее;
– вид крепления: металлическое рамное, смешанное (металлоарочное-анкерное) и анкерное.
При расположении выработок вне зоны влияния очистных работ направление их заложения не оказывает существенного влияния на их устойчивость. В зоне влияния очистных работ выработки, пройденные параллельно направлению север-юг, более устойчивые. Так, в них конвергенция со стороны кровли-почвы на 37 %, а со стороны боков на 34 % меньше, чем в перпендикулярных выработках. Анализ работы приведен на диаграмме (рис. 1).
Рис. 1. Конвергенция выработок, располагающихся в зоне влияния очистных работ
В результате проведенных исследований поведения горных выработок на шахтах Карагандинского угольного бассейна были установлены эмпирические зависимости, характеризующие влияние угла расположения выработок относительно главных горизонтальных напряжений.
Для расчета зависимости был использован метод наименьших квадратов. Общее уравнение параболы имеет вид
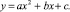(1)
Обобщая вычисления, получим систему трех уравнений с тремя неизвестными (коэффициенты перед неизвестными выражены через смешанные начальные моменты)
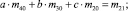
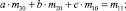(2)
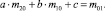
Для того чтобы найти коэффициенты a, b, c в уравнении параболы (1), нужно вычислить все компоненты, входящие в систему (2), и решить ее. Уравнение аппроксимирующей параболы имеет вид (график зависимости приведен на рис. 2):
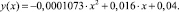(3)
Сравнение фактических yi и теоретических yТ значений конвергенций, рассчитанных по уравнению параболы, свидетельствует об удовлетворительном их совпадении.
Определим дисперсии: случайных отклонений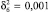 
, исходных значений 
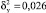, учтенная параболической зависимостью 
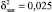. Корреляционное отношение составит h = 0,98, индекс детерминации d = 0,96, доля вариации Y за счет Х.
Найдем стационарные точки функции y(x) (3). Для этого составим уравнение, продифференцировав y(x) по аргументу х:
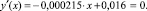
Решая которое, получим стационарную точку x0 = 74,557 ≈ 75°. Найдем вторую производную заданной функции y(x): y″(x) = –0,000215. Так как y″ < 0, то в точке хо имеет место максимум (согласно достаточному условию экстремума) (рис. 2).
Определение зависимости конвергенции боков от угла заложения выработок относительно главных максимальных горизонтальных напряжений.
Исследовано также влияние направления заложения выработок относительно главных горизонтальных напряжений на конвергенцию боков. Данная зависимость также определяется параболическим уравнением (рис. 2):
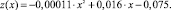(4)
Определим дисперсии: случайных отклонений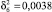 
, исходных значений 
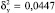, учтенная параболической зависимостью 
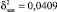. Корреляционное отношение h = 0,96, индекс детерминации d = 0,92, доля вариации Z за счет Х.
Cтационарной точкой функции z(x) (4) является x0 = 72,7 ≈ 73°. Также найдем вторую производную заданной функции z(x): z″(x) = –0,00022. Так как z″ < 0, то в точке x0 имеет место максимум (рис. 2).
Произведем определение напряжений по найденным из эксперимента перемещениям. Можно, используя уравнения теории упругости, перейти от перемещений к напряжениям. Формулы (5) дают возможность вычислить деформации
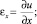
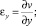
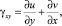(5)
и далее по закону Гука (6) определены напряжения σx, σy и txy.
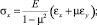
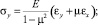(6)
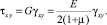
Установлены зависимости напряжений σy, σх, txy от угла заложения выработки, которые приведены в формулах (7), (8), (9). Напряжения заданы в МПа.
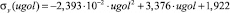[МПа]; (7)
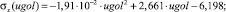(8)
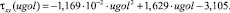(9)
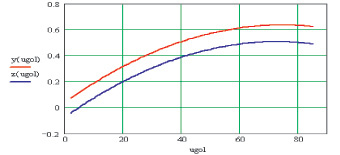
Рис. 2. Зависимость конвергенции кровли и почвы y(ugol), а также конвергенции боков z(ugol) от угла заложения выработок относительно главных горизонтальных напряжений
Коэффициенты корреляции составляют r = 0,9.
Графики зависимостей напряжений от угла заложения выработки представлены на рис. 3.
Рис. 3. Графики зависимостей напряжений σy, σx, txy от угла заложения выработок
Как видно из графиков (рис. 3), наибольшее влияние угол заложения выработки оказывает на σy. Максимальное значение 121,0 МПа – напряжение σy достигает при значении угла заложения 71°. Для σx и txy имеет место максимум при значении угла 70°, значения в точке максимума составляют 86,5 и 53,7 МПа соответственно. Таким образом, максимальное значение напряжения σy в 1,4 раза больше, чем максимальное значение σx, и в 2,3 раза больше, чем максимальное значение txy. В зоне от 0 до 70° – функция возрастает, далее идет на убывание (используется шкала от 0 до 90°).
Для уменьшения времени расчетов при определении напряжений в зависимости от угла заложения выработки и от значения модуля упругости окрестности выработок разработано программное обеспечение. Интерфейс основного окна программы представлен на рис. 4.
Рис. 4. Основная форма программы
Основная форма программы позволяет вычислить напряжения и конвергенции в зависимости от угла заложения выработки. Результаты выводятся в табличной форме и в виде графика, также можно их сохранить в отдельном файле и просмотреть в наглядном виде на дополнительной форме (рис. 5).
Рис. 5. Форма для вывода значений напряжений
Для вывода значений напряжений использован метод конечных элементов.
Библиографическая ссылка
Демин В.Ф., Яворский В.В., Демина Т.В. АНАЛИЗ ДЕФЕКТНОСТИ ВЫЕМОЧНЫХ ВЫРАБОТОК // Современные наукоемкие технологии. – 2015. – № 9. – С. 21-24;URL: https://top-technologies.ru/ru/article/view?id=35111 (дата обращения: 21.11.2024).