Причинами сбоев работы информационной системы может быть воздействие внешних дестабилизирующих факторов на линию связи канала передачи данных, вызывающие отклонение параметров уровней кодированного сигнала в среде передачи данных линии связи локальной вычислительной сети с выхода цифрового модема, функциональные нарушения в декодирующих системах, а также ошибки непосредственно в оконечных устройствах (сетевой карте, компьютере, концентраторе и т.д.).
Цель работы – построение модели автоматизированного контроля линии связи канала передачи данных локальной вычислительной сети.
В работе [2] модель оперативного контроля была построена на основе анализа параметров цифровых видеосигналов и аналоговых сигналов, модулированных многоуровневой квадратурной амплитудной фазовой модуляцией [4].
Цифровое преобразование сигналов подразумевает двоичное кодирование сигналов. Когда же нужно получить высокую скорость передачи данных в условиях ограниченной полосы, прибегают к методам повышения информационной емкости передаваемых символов. Одним из таких методов является многоуровневая система, когда каждый сигнал может принимать несколько уровней амплитуды в зависимости от значения исходного символа [1] (рис. 1).
Сложность синтеза модели автоматизированного контроля линии связи канала передачи данных локальной вычислительной сети заключается в том, что необходимо произвести «совмещение» в единой системе уравнений параметры сигналов с цифровой амплитудной модуляцией (рис. 1) [6] в линии связи канала передачи данных (ЛСКПД) и цифровые сигналы оконечных устройств [4].
Решение данной задачи возможно, если использовать функциональную модель информационной системы. В функциональной модели автоматизированного контроля и диагностирования линии связи канала передачи данных локальной вычислительной сети (рис. 2) особенностью построения и работы является наличие двух входов контролирующей системы, один из которых является одновременно выходом анализируемой системы – ЛСКПД и одновременно выходом анализируемой динамической системы – сетевой карты, а другой вход контролирующего объекта является выходом оконечного устройства [5].
Объектом исследования будет являться цифровой модем, в качестве которого может использоваться сетевая карта персонального компьютера.
Так как параметры ЛСКПД подвержены воздействию дестабилизирующих факторов и не статичны, а параметры анализируемой системы квазидетерминированы, необходимо «расщепление» модели объекта, причем с дальнейшим «совмещением» по параметрам сигналов с выхода оконечной аппаратуры и сигналов с выхода цифрового модулятора.
Сигнал S(t) – оригинал, которому соответствует функция S(p), называемая изображением
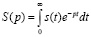. (1)
Переменная в этой формуле имеет смысл комплексной частоты p = α + jω.
Для сигналов, которые подчиняются условию (1), можно применить метод Лапласа [6]. Например, одиночный прямоугольный импульс, длительностью τ может быть представлен в виде:
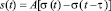. (2)
Используя свойства линейности и запаздывания для преобразования Лапласа, изображение S(p) сигнала S(t) можно записать в виде
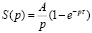(3)
Тогда спектральная плотность видеоимпульса будет иметь вид
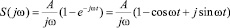, (4)
а ее модуль
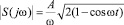. (5)
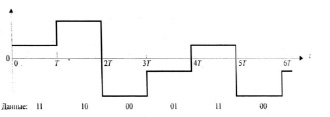
Рис. 1. Осциллограмма многоуровневого цифрового сигнала
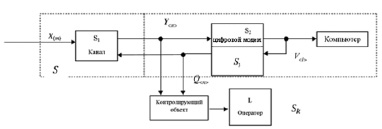
Рис. 2. Функциональная модель автоматизированного контроля и диагностирования линии связи канала передачи данных локальной вычислительной сети
В самом общем виде модель объекта может быть представлена упорядоченным множеством [3]:
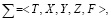
где T – множество моментов времени t, в которые наблюдается объект;
X, Y – множество входных и выходных сигналов X<m> Y<l> соответственно.
Элементы вектора X<m> в зависимости от его природы являются переменными управления или возмущениями;
z – множество состояний Z<n> объекта. Элементы вектора Z<n> являются переменными состояниями объекта или фазовыми координатами, а сам вектор Z<n> – вектор состояний. Множество векторов динамической системы составляет пространство состояний (фазовое пространство). Всякое состояние (не как вид технического состояния, а положение объекта как абстрактной динамической системы в некотором пространстве в рассматриваемый момент времени) объекта Z<n> характеризуется в каждый момент времени t∈T набором переменных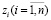 
, изменяющихся под влиянием воздействий и внутренних возмущений, обусловленных, например, отказами отдельных элементов объекта.
F – оператор переходов, отражающий механизм изменения объекта под действием внутренних и внешних возмущений, то есть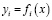 
; 
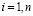, или в векторной форме 
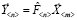. В явном виде оператор F не определяется, а оценивается принадлежность состояния объекта, характеризуемого оператором F, к одному из априорно заданных видов технического состояния:
; 
; 
.
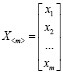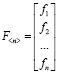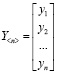Состояние объекта как динамической системы и его техническое состояние не являются эквивалентными понятиями. Техническое состояние объекта – это совокупность таких признаков, по которым можно судить о функциональной пригодности объекта, т.е. установить, является ли в данный момент объект исправным или неисправным, работоспособным или неработоспособным, правильно функционирующим или неправильно функционирующим и т.д. [3].
Состояние же объекта есть набор таких переменных, которые хотя и полностью определяют положение объекта как абстрактной динамической системы в некотором пространстве в рассматриваемый момент времени, но сами по себе не позволяют установить, правильно ли функционирует объект и исправен ли он. Для того, чтобы вынести такое суждение, необходимо сопоставить каждую переменную состояния объекта с некоторым конкретным значением, характеризующим уровень работоспособности (исправности) объекта или вид наблюдаемого в нем дефекта. Только на основании результатов сопоставления всех переменных состояний объекта с априорно заданными их значениями можно отнести это состояние к тому или иному виду его технического состояния. Однако такое сопоставление не всегда осуществимо, так как переменные состояния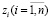 
в общем случае являются некоторыми абстрактными переменными, физическая природа которых не всегда оказывается известной, а их измерение не всегда возможно.
В отличие от них выходные переменные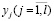 
можно наблюдать и измерять, поскольку они являются вполне конкретными физическими величинами (токами, напряжениями, угловыми и линейными перемещениями и т.д.). В этом отношении выходные сигналы являются более удобными для использования их в качестве признаков при определении технического состояния объекта, т.е. в качестве диагностических признаков. Иными словами, определение технического состояния объекта практически осуществимо не в пространстве переменных состояния 
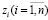, а в пространстве выходных сигналов 
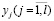или других переменных, являющихся конкретными физическими величинами (например, параметров объекта).
Возникает неопределенность в необходимости использования выходных сигналов в качестве диагностических признаков динамических систем и заданием их значений для различных видов технического состояния объекта, в частности, их номинальных значений для различных режимов нормального функционирования. Можно сформулировать, что всякому изменению вектора выхода Y<l> при фиксированном векторе X<m> соответствует определенное изменение вектора состояния объекта, т.е.
;
; 
.
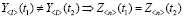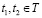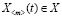Задача. Пусть первый контролируемый объект (ЛСКПД) S1 динамической системы S, представляет собой динамическую подсистему, которая в ответ на векторное входное воздействие X<m> вырабатывает выходные сигналы (y1,y2,…,yn), составляющие вектора выходов Y<n>, которые, в свою очередь, являются входными воздействиями на второй контролируемый объект (сетевая карта) S2 динамической системы S, представляющий собой вторую динамическую подсистему, вырабатывающую выходные сигналы (b1,b2,…,b1), составляющие вектора выходов V<l>, цифровой модем осуществляет «обратное» преобразование цифрового сигнала в многоуровневый кодированный сигнал, соответственно на выходе кодера будут присутствовать выходные сигналы (q1,q2,…,qn), составляющие вектора Q<n>.
Требуется построить модель Sk, такую, чтобы ее выходы совместно с выходами объекта S удовлетворяли заданному алгебраическому соотношению вида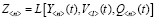 
, инвариантную к входному воздействию X<m>(t).
Составим эквивалентные матрицы.
Матрица системы S2
,
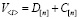где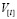 
– матрица кодов; 
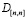– матрица приращений уровней амплитуд многоуровневого сигнала в ЛСКПД, обусловленных мультипликативными и аддитивными помехами; 
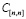– матрица уровней амплитуд уровней выходных сигналов цифрового модема в ЛСКПД.
Матрица приращений амплитуд уровней:
;
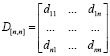матрица амплитуд уровней:
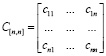
где dnn – приращение уровней многоуровневого сигнала, а cnn – амплитуда уровней многоуровневого сигнала, соответствующая определенным цифровым кодам, определяемым протоколом кодирования.
Наиболее употребительной моделью динамических объектов являются дифференциальные уравнения (ДУ). Необходимо использовать ДУ в частных производных, так как в дифференциальные уравнения, описывающие информационную систему передачи данных, входят функции нескольких аргументов.
Запишем дифференциальные уравнения модели динамической системы, представленной на рис. 1 в нормальной форме Коши.
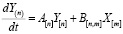– вид дифференциального уравнения для многомерного динамического линейного объекта (ЛСКПД) S1.
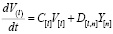– вид дифференциального уравнения для многомерного динамического линейного объекта (декодера сетевой карты) S2, причем приращение 
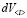будет обозначать изменение кодовой структуры цифрового видеосигнала на выходе декодера сетевой карты.
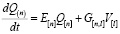– вид дифференциального уравнения для многомерного динамического линейного объекта (кодера) S3.
Исходя из вышеизложенного можно построить систему уравнений модели автоматизированного контроля линии связи канала передачи данных локальной вычислительной сети:
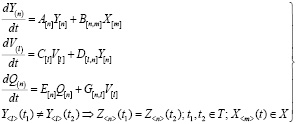
с начальными условиями
.
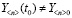При использовании данной модели множества входных и выходных сигналов X<m> Y<l> соответственно, можно использовать аналитические выражения 1, 2, 3 в зависимости от необходимости исследования воздействия дестабилизирующих факторов или на уровни амплитуд сигналов в ЛСКПД, или на ошибки кодов на входе оконечной аппаратуры, или на изменение спектральных характеристик сигналов в ЛСКПД.
Полученная математическая модель позволяет при проведении дальнейших исследований учитывать влияние отклонения параметров многоуровневых сигналов в ЛСКПД в результате воздействия мультипликативных и аддитивных помех на изменение кодовых структур сигналов на выходе цифрового модулятора, а также влияние дефектов в цифровом модуляторе и оконечных устройствах канала передачи данных на результаты оперативного контроля.
Библиографическая ссылка
Власов В.И., Власов С.В. МОДЕЛЬ АВТОМАТИЗИРОВАННОГО КОНТРОЛЯ ЛИНИИ СВЯЗИ КАНАЛА ПЕРЕДАЧИ ДАННЫХ ЛОКАЛЬНОЙ ВЫЧИСЛИТЕЛЬНОЙ СЕТИ // Современные наукоемкие технологии. – 2015. – № 8. – С. 13-17;URL: https://top-technologies.ru/ru/article/view?id=35089 (дата обращения: 21.11.2024).