В ряде работ по бесплатформенным инерциальным системам затрагивались вопросы их моделирования с целью оценки эффективности. Для симуляции БИНС часто применяют программную среду Matlab [1–5]. В статье [4] авторы рассмотрели математическое моделирование и симуляцию составной части БИНС – бесплатформенной системы ориентации (БСО). В продолжение научных исследований предлагается аналогичный материал по БИНС. Реализация алгоритма БИНС является на порядок сложнее по сравнению с алгоритмом БСО, т.к. в этом случае, во-первых, алгоритм БСО уже является составной частью алгоритма БИНС, во-вторых, приходится создавать и использовать довольно сложную динамическую модель движения объекта по отношению к Земле.
В данной статье рассматривается моделирование БИНС в инструментальной среде Matlab Simulink с целью проверки математических моделей и получения результатов исследования эффективности БИНС при их работе в различных динамических режимах. Исполнение математических моделей БИНС в Simulink позволяет получить понятную визуальную модель системы и реализовать многочисленные операции дифференцирования и интегрирования более гибко на стандартных элементах.
Статья имеет, прежде всего, практическую направленность, позволяющую повторить предлагаемые модели и схемы, получить результаты симуляции и оценить эффективность алгоритмов БИНС. Исследования авторы проводили на основе многочисленных источников информации, некоторые из которых отражены в списке литературы, и собственных разработок.
Математическая модель БИНС
Алгоритмы БИНС подробно описаны в работах как отечественных, так и зарубежных авторов, например [5, 6]. Алгоритм навигации служит для определения положения центра масс подвижного объекта относительно земной системы координат. Для решения задачи навигации используются данные об ускорении объекта, измеренные акселерометрами в связанной системе координат. Основная идея инерциальной навигации – это двукратное интегрирование измеренных ускорений. Способом построения БИНС является размещение инерциальных датчиков акселерометров и гироскопов непосредственно на борту подвижного объекта, а функции гиро стабилизированной платформы, привязанной к земной системе координат, выполняет бортовой вычислитель.
Рассмотрим движение подвижного объекта (беспилотного летательного аппарата – БПЛА) на высоте h со скоростью V. Алгоритм БИНС основан на кинематических уравнениях подвижного объекта в земной системе координат:
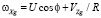 ;
;
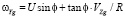 ;
;
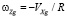 , (1)
, (1)
где VZg, VXg – составляющие линейной скорости объекта соответственно вдоль оси Zg и Xg географической системы координат; U – угловая скорость вращения Земли; φ – широта местоположения объекта; R – средний радиус земного эллипсоида.
На основе (1) угловая скорость движения объекта относительно Земли определяется следующими соотношениями:
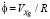 ;
;
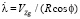 ;
;
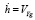 . (2)
. (2)
Для получения координат объекта φ, λ, h в географической системе необходимо иметь информацию о линейных скоростях объекта VXG, VYG, VZG. Эту информацию получают путем интегрирования соответствующих ускорений. В БИНС датчики ускорений – акселерометры устанавливают по осям связанной системы координат, они измеряют кажущееся ускорение. Следует отметить, что абсолютное ускорение имеет следующие составляющие:
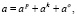 (3)
(3)
где ap, ak, ao – составляющие ускорения соответственно переносного, кариолисова, относительного.
Кариолисово ускорение возникает при взаимодействии переносной угловой скорости вращения Земли и линейной скорости объекта. Проекции кариолисова ускорения на оси OXgYgZg имеют вид
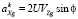 ;
;
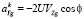 ;
;
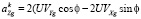 . (4)
. (4)
Относительное ускорение возникает при движении объекта вокруг Земли и при изменении линейной скорости, его составляющие на оси OXgYgZg имеют вид
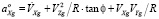 ;
;
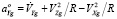 ;
;
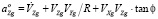 . (5)
. (5)
Переносное ускорение вызвано угловой скоростью вращения Земли, и его составляющие в пересчете в земную систему координат определяются соотношениями:
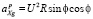 ;
;
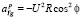 ;
;
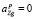 . (6)
. (6)
При сложении вектора переносного ускорения с вектором g гравитационного поля Земли получим вектор ускорения силы тяжести (0, g, 0).
Акселерометры, жестко установленные в связанной системе координат, измеряют проекции кажущегося ускорения, в которых учитываются все три составляющие: кариолисово, относительное и ускорения силы тяжести. Путем пересчета кажущегося ускорения в географическую систему координат получают составляющие nXg, nYg, nZg:
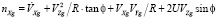 ;
;
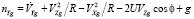 ;
;
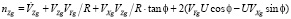 . (7)
. (7)
где V’Zg, V’Yg, V’Xg – составляющие ускорения объекта соответственно по осям Zg, Yg, Xg географической системы координат.
Для использования в навигационном алгоритме БИНС показаний акселерометров из них необходимо извлечь V’Zg, V’Yg, V’Xg – составляющие ускорения объекта соответственно по осям Zg, Yg, Xg географической системы координат путем удаления из них вредных составляющих: ускорения Криолиса, относительного ускорения и ускорения силы тяжести.
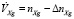 ;
;
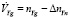 ;
;
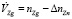 , (8)
, (8)
где ΔnZg, ΔnYg, ΔnXg – вредные составляющие: ускорения Криолиса, относительного ускорения и ускорения силы тяжести соответственно по осям Zg, Yg, Xg географической системы координат:
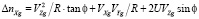 ;
;
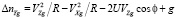 ;
;
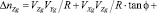
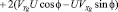 . (9)
. (9)
Навигационный алгоритм БИНС при интегрировании соотношений (8) вычисляет составляющие линейных скоростей.
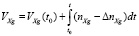 ;
;
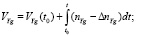 (10)
(10)
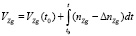 ,
,
где VZg(t0), VYg(t0), VXg(t0) – составляющие вектора скорости в начальный момент времени t0.
Угловые координаты объекта и высота определяются при вторичном интегрировании (2) с учетом начальных значений координат и высоты:
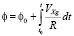 ;
;
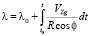 ;
;
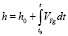 , (11)
, (11)
где φ0, λ0, h0 – составляющие координат объекта в начальный момент времени t0.
Навигационный алгоритм БИНС, основанный на приведенных формулах, представлен на рис. 1 в виде структурной схемы.
В схему добавлен конвертор вектора кажущегося ускорения с акселерометров для пересчета в земную систему координат. Этот конвертор работает на основе кватернионного умножения L*N*L, где L, N – кватернионы соответственно углов Эйлера и ускорений. На вход конвертора поступает вектор N = [nX, nY, nZ], на выходе получается вектор Ng = [nXg, nYg, nZg], необходимый для работы БИНС.
Математическая модель БСО, хотя и не включена в схему БИНС, является составной частью алгоритма БИНС, т.к. определение угловой ориентации подвижного объекта необходимо для решения задачи навигации.
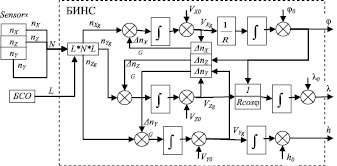
Рис. 1. Структурная схема алгоритма БИНС
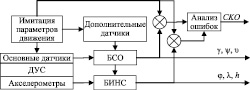
Рис. 2. Схема моделирования БСО и БИНС (γ, ψ, υ – оценки углов; φ, λ, h – оценки координат)
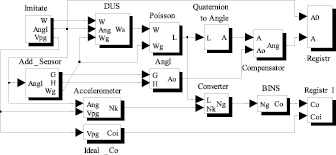
Рис. 3. Структурная схема моделирования БИНС и БСО
Схема моделирования БИНС представлена на рис. 2.
Схема содержит следующие блоки.
1. Блок имитации параметров движения объекта, который осуществляет имитацию углового движения объекта с учетом изменения углов υ, γ, ψ по синусоидальным законам и с учетом движения объекта вдоль Земли с линейной скоростью. Также этот блок осуществляет имитацию абсолютного ускорения объекта с учетом эволюции ускорений по осям географической системы координат по синусоидальным законам;
2. Блок основных датчиков (ДУС и акселерометры) выдает три составляющих абсолютной угловой скорости (ωXS, ωYS, ωZS) и три компоненты кажущегося ускорения в связанной системе координат (nX, nY, nZ);
3. Блок дополнительных датчиков вычисляет данные об угловом движении объекта на основе избыточной информации (в данном случае с акселерометров и магнитометров);
4. Блок БСО, осуществляет решение кинематических уравнений углового движения объекта на основе информации, получаемой с ДУС и с дополнительных датчиков;
5. Блок БИНС осуществляет интегрирование скомпенсированных сигналов акселерометров и выдает координаты объекта в виде параметров φ, λ, h;
6. Разностные элементы, вычисляют ошибки оценивания углов Эйлера и координат φ, λ, h;
7. Блок анализа ошибок, вычисляет средние квадраты ошибок оценивания углов ориентации и координат объекта и их предельные значения. Кроме того, блок анализа позволяет получить графики оценок углов и координат объекта на фоне их истинных значений для визуального анализа точности.
Моделирования БИНС в среде Matlab Simulink
Для исследования работоспособности алгоритма БИНС в комплексе с БСО необходимо придерживаться схемы моделирования, разработанной в среде Matlab Simulink [3]. Только требуется добавить блок БИНС с оценкой его ошибок. Модернизированная схема моделирования представлена на рис. 3.
На схеме рис. 3 в качестве основных датчиков представлены ДУС и акселерометры, играющие основную роль в работе БИНС. В качестве дополнительных датчиков используются, как и ранее, магнитометры и акселерометры (для алгоритма БСО). На схеме рис. 1 была показана связь алгоритма БСО с алгоритмом БИНС. Эта связь необходима при реализации алгоритма БИНС на основе кватернионов. В этом случае легко выполняется пересчет показаний акселерометров в земную систему координат.
На схеме имеется блок имитации исходных данных для задания углов ψ, υ, γ и параметров ускорения объекта в земной системе координат (в данном случае по синусоидальным законам в разрешенных пределах). Задание других многочисленных параметров для функционирования БСО и БИНС осуществляется с помощью управляющей программы BINS.m.
На схеме использованы как традиционные блоки, применяемые ранее при моделировании БСО [4] (Imitate, DUS, Add_Sensor, Poisson, Quaternion to Angle, Angi, Compensator, Registr), так и новые (Accelerometer, Ideal_Co, Converter, BINS), предназначенные для реализации алгоритма БИНС и его моделирования. Некоторое развитие получил блок Imitate, в который добавлена схема моделирования ускорений объекта в земной системе координат. На схеме использованы синусоидальные датчики, выдающие параметры ускорений Vpx, Vpy, Vpz, которые настроены на конкретные амплитуды, начальные значения и частоты.
Блок моделирования ускорений Accelerometer, имеющий место на схеме рис. 3, работает на основе данных о составляющих ускорения объекта соответственно по осям Zg, Yg, Xg географической системы координат (V’Zg,V’Yg,V’Xg), данных об угле широты места φ и значении ускорения свободного падения g. Сначала в блоке Accelerometer вырабатываются сигналы по известным формулам (7), затем они пересчитываются в данные для выходов акселерометров – Nk с помощью матрицы направляющих косинусов Ao. Формула (7) содержит все составляющие кажущегося ускорения в земной системе координат: Ng=[nXg, nYg, nZg]. Далее, пересчитав компоненты nXg, nYg, nZg в связанную систему координат, получим компоненты кажущегося ускорения непосредственно с выходов датчиков – акселерометров (nX, nY, nZ).
Для получения данных в виде вектора Ng требуется конвертировать данные с акселерометров в земную систему координат. Это осуществляется с помощью конвертора Converter, который функционирует на основе кватернионного соотношения L*N*L.
Блок BINS на основе данных акселерометров в виде Ng вычисляет координаты объекта: φ, λ, h. Схема блока BINS представлена на рис. 4.
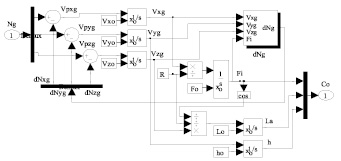
Рис. 4. Схема вычисления координат в земной системе
В схему блока BINS встроена субсистема dNg, вычисляющая ошибки акселерометров связанные с кажущимся ускорением. Эти ошибки компенсируются перед интегрированием сигналов ускорений – в итоге получаются истинные координаты объекта.
В блок БИНС подается вектор кажущегося ускорения, полученный в земной системе координат: Ng = [nXg, nYg, nZg], на выходе в результате компенсации ошибок и интегрирования получается вектор координат Co = [φ, λ, h]. Схема субсистемы dNg работает на основе формул (9).
Блок вычисления идеальных координат объекта – Ideal_Co на основе информации об идеальных значениях скорости БПЛА, полученной в земной системе координат путем интегрирования истинных ускорений БПЛА, предварительно вычисляет идеальные значения координат БПЛА: φ, λ, h.
Анализ результатов моделирования БИНС
Проведено моделирование алгоритма БИНС для конкретного режима полета летательного аппарата. Были заданы следующие исходные данные по начальным параметрам и динамике.
По угловому положению: законы изменения углов рыскания, тангажа и крена заданы синусоидальными с такими же параметрами, как и в предыдущих примерах: рыскание – начальное значение ψo = arctg(Vzg/Vxg), амплитуда Aψ = 1о, частота wψ = 0,1 Гц; тангаж – начальное значение υo = 0,131 о, амплитуда Aυ = 1,5о, частота wυ = 0,15 Гц; крен – начальное значение γo = 0,131о, амплитуда Aγ = 0,3о, частота wγ = 0,2 Гц.
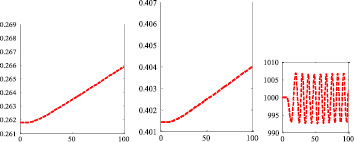
Рис. 5. Изменение угла широты, угла долготы и высоты полета
По ускорениям ЛА на основе синусоидальных законов в земной системе координат: по оси Xg: с амплитудой Vpxa = 4,6 м/с2; начальным значением Vpxb = 0 м/с2; частотой Vpxw = 0,5 Гц; по оси Yg: с амплитудой Vpya = 2,5 м/с2; начальным значением Vpyb = 0 м/с2; частотой Vpyw = 0,6 Гц; по оси Zg: с амплитудой Vpza = 3,5 м/с2; начальным значением Vpzb = 0 м/с2; частотой Vpzw = 0,4 Гц.
По скоростям в земной системе координат – начальные значения: Vxo = 250; Vyo = 0; Vzo = 150. По навигационным координатам – начальные значения: φo = 15 град; λo = 23 град; ho = 1000 м.
Проводилась симуляция заданного режима полета и совместной работы БСО и БИНС в течение 100 с, были получены графические результаты, представленные на рис. 5. На рис. 5 представлено изменение угла широты φ от начального значения 0,2618 радиан (15 град.) до 0,2658 радиан (15,23 град.), угла долготы λ от начального значения 0,2618 радиан (15 град.) до 0,2658 радиан (15,23 град.) и высоты полета h от начального значения 1000 м по синусоидальному закону с амплитудой около 7 м.
Задачей исследования эффективности БИНС является анализ точности оценивания координат подвижного объекта. С этой целью на основе информации об идеальных значениях скорости БПЛА, полученной в земной системе координат путем интегрирования истинных ускорений, предварительно вычисляются идеальные значения координат ЛА: φ, λ, h (рис. 2).
По формулам математической статистики получены средние квадраты ошибок (СКО) по рассматриваемым координатам: CKOfi = 1,4∙10-16; CKOla = = 3,9∙10-17; CKOh = 2,0∙10-8. Предельные ошибки в процентах составили: dFi = 4,5∙10-6 %; dLa = 1,6∙10-6 %; dh = 1,4∙10-5 %.
Выводы
Моделирование алгоритма БИНС проведено с помощью программной среды Matlab Simulink. В качестве результатов моделирования приведены графики основных процессов и численные результаты по ошибкам оценивания углов ориентации. Результаты компьютерного эксперимента подтверждают эффективность алгоритма БИНС в системах определения пространственного положения маневренных подвижных объектов в широком диапазоне сигналов и шумов. Ввиду незначительного расхождения результаты в виде графиков оценок практически совпадают с реальными углами, что доказывает эффективность компенсации ошибок дрейфа показаний гироскопов. В итоге компенсация дрейфа гироскопов, применяемая в алгоритме оценивания на основе кватернионов дает высокую точность оценок (не хуже 0,000005 %).
Библиографическая ссылка
Волков В.Л., Жидкова Н.В. МОДЕЛИРОВАНИЕ БЕСПЛАТФОРМЕННОЙ НАВИГАЦИОННОЙ СИСТЕМЫ // Современные наукоемкие технологии. 2015. № 7. С. 13-18;URL: https://top-technologies.ru/ru/article/view?id=35069 (дата обращения: 26.01.2026).



