Для эффективного функционирования различных производственных объектов страны, в том числе малых предприятий (МП) существенное значение имеет выбор оптимальной стратегии их развития в условиях рыночной экономики. Одним из важнейших факторов функционирования и развития данных объектов является эффективное использование кредитных или заемных средств. Для решения указанных проблем применение классических экономико-математических моделей не приводит к желаемым результатам из-за высокой степени нестационарности и стохастичности основных параметров и показателей данной сферы производства. В предлагаемой работе на базе известных подходов к построению имитационных моделей производства, заложенных в основополагающих трудах [1, 2] и других авторов [7, 8], а также в предыдущих публикациях авторов данной статьи [5, 6], предлагается обобщенная имитационная модель функционирования малого предприятия для анализа влияния нестационарности и случайности спроса и предложения на эффективность его работы.
Функциональная структура производства и реализации продукции МП
Функциональная структура малого предприятия как системы представлена на рисунке и наглядно отражает как производственные, так и информационно-управляющие функции.
Интенсивности роста объема производства и реализации продукции, повышение ее качества непосредственно влияют на конечные результаты функционирования предприятия, поэтому анализ всех показателей функциональной структуры имеет важное значение.
Построение модели функционирования системы
Для описания и анализа динамики функционирования системы целесообразно [8, 9] построить эконометрическую модель в виде рекуррентных соотношений.
Начнем с построения уравнения блока «Приобретение материалов»
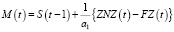, (1)
где М – объемы приобретенного сырья, ZNZ– желательный запас сырья, FZ – фактический запас сырья, S – объемы реализации продукции, a1 – запаздывание регулирования запасов сырья.
Блок «Производство продукций» описывается уравнением
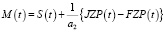, (2)
где W – объем производства, JZP и FZP – соответственно желательный и фактический запасы продукций, a2 – запаздывание регулирования запасов продукции, t – текущий момент времени, t-1 – предыдущий момент времени.
В блоке «Реализация» осуществляется моделирование интенсивности продаж продукции как непрерывной или целочисленной случайной величины.
Для оценки кассовой наличности воспользуемся выражением
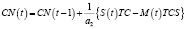,(3)
где CN – кассовая наличность, TC – цена продукции, TCS – цена сырья.
Суммарные издержки на налоги и выплату процентов определяются по формуле
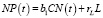, (4)
где b1 – налоговая ставка, а rLL – выплата процентов по кредиту L.
Для вычисления прибыли PR используется выражение
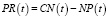. (5)
Все представленные уравнения составляют модель функционирования исследуемой системы.
Моделирование объемов продаж продукции
Такое моделирование может быть реализовано, например, методом обратной функции моделирования случайных величин, основанным на теореме 1 [5]: «Случайная величина S, реализации которой определяются из выражения
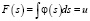или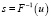 
,
где u – случайное число, равномерно распределенное в интервале [0, 1], имеет плотность распределения j(s)» или основным методом моделирования целочисленных величин, основанным на теореме 2: «Величина S, заданная в виде таблицы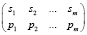 
, наступает с вероятностью pk при выполнении условия u∈Dk, где Dk = pk».
В случае невозможности реализации преобразования или при задании законов распределения параметра S в графическом виде или в табличной форме можно воспользоваться методом исключения Джона фон Неймана, принцип работы которого непосредственно вытекает из теоремы 3 «Пусть u1 и u2 – случайные числа, равномерно распределенные в интервале [0, 1] и s = a + u1(b–a), y = Mu2, s∈ [a, b], тогда случайная величина S, определенная из условия S = s при y < j(s), имеет плотность распределения φ(s)». Доказательства данных теорем можно найти в [6].
Если функция плотности j(s) относится к одному из известных стандартных теоретических законов распределения, то для моделирования значений S можно воспользоваться формулами, приведенными в таблице [6].
Динамическая модель анализа жизнедеятельности малого предприятия
Определяющим фактором жизнедеятельности малого предприятия, очевидно, является эффективность использования денежных средств. Опишем уравнения, характеризующие изменения денег и кредитов:
,
,
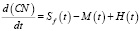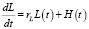где Sf(t) – объем реализации продукции в денежном выражении Sf(t) = S(t)TC, rL – банковская ставка, H(t) – заемные средства.
Предполагается, что для обеспечения непрерывности производственных расходов необходим запас финансов [3]
,
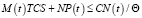где Q – коэффициент ликвидности.
Рентабельность малого предприятия зависит от динамики цен на сырье и его продукцию. Обозначим прогнозируемую величину инфляции цен через і. Суммарный коэффициент дисконтирования, учитывающий инфляцию цен, обозначим через
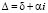, (6)
где d – коэффициент дисконтирования, а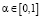 
.
Доходы малого предприятия с учетом инфляции цен на продукцию прогнозируются по экспоненциальному закону с интенсивностью γ.
.
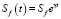Функциональная структура системы
Формулы моделирования основных теоретических распределений случайных величин
|
Распределение |
Функции плотности |
Формула для моделирования |
|
Нормальное |
– ∞ < τ < ∞ |
|
|
Равномерное |
|
τ = a + u(b – a) |
|
Экспоненциальное |
f(τ) = λe–λτ, τ ≥ 0 |
|
|
Линейное |
|
|
|
Гамма |
k > 0, τ ≥ 0 |
|
,
, 
, 
, α > 0,
Сформулируем задачу максимизации суммарных доходов SS малого предприятия
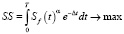; (7)
;
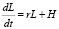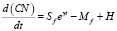; (8)
CN ≥ Mf + NP, L(t) = 0, L ≥ 0, CN ≥ 0,
где Mf – денежные выражения материалов.
На основе оптимальной траектории задачи (7, 8)
,
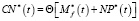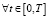, (9)
полученной по аналогии с оптимизацией потребительских расходов, рассмотренных в [3], можно привести следующие экономические интерпретации результатов деятельности малого предприятия. В зависимости от коэффициента дисконтирования малые предприятия могут иметь три варианта результатов своей деятельности.
Вариант 1. При выполнении соотношения
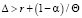(10)
малое предприятие вынуждено постоянно брать кредиты. При таком уровне коэффициента дисконтирования малое предприятие относится к нерентабельным субъектам экономики.
Вариант 2. При выполнении соотношения
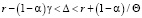(11)
малое предприятие может как привлекать кредиты, так и функционировать за счет собственных средств в краткосрочном периоде. Но с течением времени, при отсутствии финансирования, малое предприятие также становится нерентабельным.
Вариант 3. При выполнении соотношения
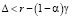(12)
малое предприятие может как брать кредиты, так и расходовать только собственные средства. При любых начальных условиях оно расплачивается с кредитными обязательствами за ограниченный отрезок времени. Кредиты нужны только для быстрого выхода на оптимальный режим работы малого предприятия.
Разработанная модель ориентирована, в основном, на применение в задачах перспективного анализа, когда необходимо выяснить допустимо возможные варианты развития исследуемых экономических объектов. Также предлагаемая модель при условии ее соответствующей модификации может быть пригодна не только для прогнозирования, но и для текущего управления деятельностью малого предприятия.
Алгоритм моделирования процесса функционирования МП
Алгоритм моделирования процесса функционирования малого предприятия включает следующие шаги:
Шаг 1. Моделирование объемов и вектора моментов времени поступления кредитов и займов.
Шаг 2. Вычисление объемов приобретенных материалов по (1).
Шаг 3. Вычисление объемов выпуска продукции по (2).
Шаг 4. Имитация объемов реализации продукции как непрерывной или целочисленной случайной величины.
Шаг 5. Вычисление значения кассовой наличности по (3).
Шаг 6. Вычисление суммарных издержек на налоги и выплата процентов по (4).
Шаг 7. Вычисление прибыли по (5).
Шаг 8. Анализ соответствия полученных по формулам (1-5) значений параметров деятельности МП с оптимальной траекторией (9) задачи (7,8).
Шаг 9. Определение из выражения (9) фактических значений суммарного коэффициента дисконтирования и параметра ликвидности.
Шаг 10. Анализ результатов деятельности малого предприятия по условиям (10–12).
Предлагаемый алгоритм оценки эффективности предпринимательской деятельности малого предприятия позволяет дать объективную, структурированную экономическую оценку ее результативности. Разработанный алгоритм позволит руководителям экономически взвешенно подходить к процессу организации предпринимательской деятельности, оперативно принимать управленческие решения, а также корректировать направления деятельности малого предприятия в целом на основе проведения анализа эффективности его функционирования с учетом факторов экономической среды.
Имитационное моделирование на основе рассмотренной экономико-математической модели может использоваться для решения различных задач прогнозного характера в рамках исследования функционирования различных производственных объектов в условиях нестационарности и случайности спроса и предложения на их товары и услуги.
Заключение
Малое предприятие, работая в условиях определенных ограничений, может успешно функционировать в конкурентной среде в основном за счет использования внутренних резервов, выявление которых возможно только с помощью математических моделей и алгоритмов функционирования и прогнозирования процесса производства.
Разработанная динамическая модель позволит оперативно принимать управленческие решения при разработке долгосрочных стратегий развития предприятия, а также позволит определять уровень рентабельности.
Таким образом, предложенный подход на базе методов прогнозирования и аналитико-имитационного моделирования [4] может способствовать более рациональной оценке эффективности предпринимательской деятельности малых предприятий как на стадии планирования инвестиционно-инновационного проекта, так и на стадии его реализации.
Библиографическая ссылка
Шукаев Д.Н., Ламашева Ж.Б., Токпанова К.О. ИМИТАЦИОННАЯ МОДЕЛЬ МАЛОГО ПРЕДПРИЯТИЯ // Современные наукоемкие технологии. – 2015. – № 4. – С. 66-69;URL: https://top-technologies.ru/ru/article/view?id=35017 (дата обращения: 24.11.2024).