В случае фазово-разупорядоченного состояния ультрадисперсных компонентов системы может проявляться эффект синергизма – отклонение свойства материала от величины, которая может быть получена по аддитивной схеме с учетом индивидуальных характеристик фаз [1–4]. В соответствии с моделью «концентрационной волны» [4] трибологические свойства композитов определяются размерным и наноструктурным факторами. Экспериментально установлено [5–17], что для композитов разного фазового состава наноструктурный параметр принимает значения в интервале от 0,03 до 0,17 и характеризует объемную долю наночастиц фаз твердых компонент трибосопряженных поверхностей.
Будем считать, что в общем случае состояния детерминистических модулярных структур определяются возможными кристаллическими r, наноразмерными n и фрактальными f компонентами. Множество вероятных структурных 1D состояний детерминистических модулярных структур композитов включает три основные состояния (rr ≡ r, nn ≡ n, ff ≡ f) и три пары из сопряженных состояний (rn и nr, rf и fr, nf и fn). Возможные пространственные компоненты структурных состояний поверхности проанализированы в работе [18]. Сформулированы принципы формирования возможных структурных состояний из наноразмерных компонент с учетом свойств множества соответствующих нанообъектов [19]. Проанализированы размерные характеристики возможных состояний многокомпонентных структур, включающих наноразмерную компоненту, и их влияние на свойства системы [20, 21].
Из десяти классов вероятных структурных состояний класс (n n n)) характеризует возможные структурные состояния, включающие в себя в основном только наноразмерную компоненту.
Симметрия структур Rnnn3 может описываться пространственными G33 , слоевыми G32, стержневыми G31, точечными G30 группами [22, 23]. Перечислим возможные виды состояний наноразмерного класса (n n n) и приведем сопряженные им (*) состояния.
1) (n n n) - 3D-наночастица, (n n n)* = (n n n),
2) (n n nr) - 3D-нанообъект из 1D-фрагмента структуры, (n n nr)* = (n n rn),
3) (n n nf) - 3D-нанообъект из 1D локального фрактала, (n n nf)* = (n n fn),
4) (n nr nr) - 3D- нанообъект из 2D нанофрагментов структуры, (n nr nr)* = (n rn rn),
5) (n nr nf) - 3D-нанообъект из 1D-фрагмента структуры и 1D локального фрактала, (n nr nf)* = (n rn fn),
6) (n nf nf) - 3D-нанообъект из 2D локальных фракталов, (n nf nf)* = (n fn fn).
7) (nr nr nr) - 3D-нанообъект из 3D-нанофрагментов структуры, (nr nr)* = (rn rn),
8) (nr nr nf) - 3D-нанообъект из 2D-нанофрагмента структуры и 1D локального фрактала, (nr nr nf)* = (rn rn fn),
9) (nr nf nf) - 3D-нанообъект из 1D-нанофрагмента структуры и 2D локального фрактала, (nr nf nf)* = (rn fn fn).
10) (nf nf nf) - 3D локальный фрактал, (nf nf nf)* = (fn fn fn).
Условный размерный параметр D для каждого структурного состояния может быть представлен следующим образом: D = dr D(r) + df D(f) + dn D(n), где dr, df и dn - количества соответствующих компонент одного сорта. Условный размерный параметр для кристаллической компоненты D(r) = 1, для фрактальной компоненты он полностью совпадает с фрактальной размерностью: D(f) = DimRf = Dim (GenRf) < 1, для наноразмерной компоненты D(n) = (<n>/no) < 1, если средний размер нанообъекта < no = 100 нм и D(n) = 1, если o.
Пример. Определим размерный параметр для состояния (nr nf nf), характеризующего 3D-нанообъект из 1D-нанофрагмента структуры и 2D локального фрактала. Сопряженным с ним является состояние (rn fn fn), представляющее собой 3D структуру из 1D нанофрагмента структуры и 2D локального фрактала. С учетом разложения (nr nf nf) = 1/6 [3(n n n) + (r r r) + 2(f f f)] окончательно получим D = 1/6 [9(<n>/no) + 3 + DimGenRfff1 + DimGenRfff2]. Отметим, что для сопряженного структурного состояния (nr nf nf)* = (rn fn fn) размерный параметр идентичен.
Предположим, что если компоненты структурных состояний - пространственные, то на свойство SD влияет отклонение условного размерного параметра D от мерности пространства d, т.е. величина |d-D|. Формально можно рассматривать два вида зависимостей: SD = Sd(1 + K|d-D|) и ln(SD/Sd) = K|d-D|, где коэффициент пропорциональности К обусловлен как характеристиками структурного состояния, так и характеристиками пространства, в котором существует система с данным состоянием. При расчете размерных параметров структурных состояний для отдельных компонент использовали следующие условные значения: D(r) = 1, D(f1) = D(f2) = D(f3) = 0,5, D(n1) = D(n2) = D(n3) = 0,1. Вторая зависимость от размерного параметра - экспоненциальная SD = Sd exp(K|d-D|) и является более сильной по сравнению с первой (рисунок, а). На величину |d-D| существенно влияют значения компонент D(f) и D(n1). В частности, влияние величины наноразмерной компоненты D(n) на условный размерный параметр D для каждого из десяти структурных состояний класса (n n n) показано на рисуноке, б.
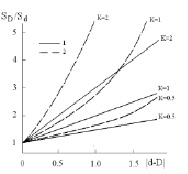 a)
a) 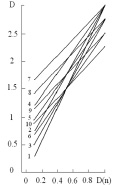 б)
б)
Влияние условного размерного параметра D структурного состояния детерминистических модулярных структур на свойства систем по зависимостям вида SD = Sd(1 + K|d-D|) (а-1) и SD = Sd exp(K|d-D|) (а-2). Влияние величины наноразмерной компоненты D(n) на условный размерный параметр D десяти структурных состояний класса (n n n) (б)
Представления о возможном влиянии комплексного состояния композитов, обусловленного как кристаллическими фазами, так и распределенными определенным образом наночастицами некоторых из этих фаз были использованы при целенаправленном поиске и интерпретации трибологических свойств поверхности композиционных материалов и покрытий на основе жидкого стекла [10–12], систем Ni-P [1-4, 13-17] и Ni-B [5–9]. Основные характеристики некоторых вероятных нанообъектов на поверхности указанных выше нанокомпозитов, обладающих антифрикционными свойствами, представлены в работах [24–36].
Библиографическая ссылка
Дерлугян П.Д., Иванова И.В., Иванов В.В., Шишка В.Г. ВОЗМОЖНЫЕ КОМПЛЕКСНЫЕ КОМПОНЕНТЫ СОСТОЯНИЙ НАНОРАЗМЕРНОГО (NNN) КЛАССА ДЕТЕРМИНИСТИЧЕСКИХ МОДУЛЯРНЫХ СТРУКТУР НАНОКОМПОЗИТОВ // Современные наукоемкие технологии. 2015. № 1-1. С. 13-15;URL: https://top-technologies.ru/ru/article/view?id=34982 (дата обращения: 17.11.2025).



