Разработанные в настоящее время аналитические методы расчета характеристик системы массового обслуживания (СМО) применимы лишь к отдельным законам распределения интервалов времени между событиями потоков.
Основой исследования фрактальных характеристик потоков мультимедийной информации в системах связи послужило большое количество измерений, проводимых на различных сетях и подтверждающих наличие самоподобия, и неадекватного расхождения между проектируемой нагрузкой и существующей [2], что приводит к завышенным оценкам и снижению показателей качества обслуживания (QoS).
Цель исследования. В силу непуассоновского характера поведения реального трафика, в качестве модели необходимо использовать СМО G/G/1, которая характеризуется произвольным распределением интервалов времени между поступлениями требований и произвольным распределением времени обслуживания требований. В дальнейшем, с точки зрения возможности использования решения уравнения Линдли [1], целесообразно рассмотреть разложение неизвестной плотности в ряды экспонент.
Целью эксперимента являлось изучение статистических характеристик сети для представления выходных параметров функционирования сетевого устройства.
Для эффективного обслуживания и наилучших показателей QoS необходимо учитывать численные значения параметров, таких как средняя задержка, джиттер, уровень потерь пакетов. Именно задержки и потери пакетов в очередях оказывают наиболее критическое влияние на разборчивость речи и качество видеоизображений [2, 3, 4, 5]. Поэтому научно-практические разработки и исследования, связанные с данной проблемой и усовершенствование или разработка новых математических моделей и алгоритмов (методов), являются важными и актуальными.
Материалы и методы исследования
К противоречию в восприятии информации, передаваемой по каналу связи, и сигнала, передающего от источника и обрабатываемого в обслуживающем устройстве, приводит к неосведомленности в структуре построения телекоммуникационной сети. Исследования современных возможностей сетей приводят к выводу, что классическая теория СМО отстает от настоящих потребностей. Учеными неоднократно доказано, что необходимо отталкиваться от имитационного или модельного представления сети, передающей мультимедийный трафик в реальном времени с минимальным значением потерь. Важным при осуществлении анализа адекватности модели сети (СМО) является ее техническая составляющая, а именно, характеристики задержки и пропускной способности. Однако в основном найти данные характеристики не представляется возможным. Эти значения задаются сразу или же пользуются приближением входных распределений к марковским СМО M/М/1, G/M/1 и M/G/1 [1]. Поэтому, поиск таких методов или аппаратов расчета, где технические характеристики системы можно было бы найти, зная лишь, что наблюдается на входе обслуживаемого устройства (функцию распределения интервалов времени поступления пакетов (в единицах времени или условных)) остается актуальной задачей.
Аппроксимация функции плотностей распределений с «тяжелым» хвостом (РТХ) с помощью полинома Лагранжа позволяет определить аппроксимирующую функцию. Следовательно, этот метод можно применить при исследовании неизвестной функции распределения времени, которой подчиняется поступающий и обслуживаемый сетевой трафик (пакеты).
Результаты исследования и их обсуждение
В данном эксперименте при анализе трафика с помощью программы-снифера WireShark были получены, в форме текстовых файлов, статистические данные, такие как интервалы времени поступления пакетов (в секундах) и длины пакетов (в байтах). Затем, по снятым статистическим данным реального потока, поступающим на вход сетевого элемента, который обрабатывает самоподобный трафик, можно получить аппроксимирующее выражение функции плотности распределения вероятностей через сумму затухающих экспонент [6].
Выборку величин представляем в виде интервалов времени между пакетами τi и величин длительности обслуживания пакетов ξj, где j – моменты поступления на обслуживание и равны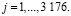 
Вычисления осуществляются с помощью пакетов программных средств Matlab версии 8.0 и EasyFit Professional, предназначенных для автоматической аппроксимации классов распределений. Аппроксимация распределений осуществляется с помощью метода максимального правдоподобия (MLE) (оценка критериев согласия (GOF) осуществлялась с помощью статистического критерия Колмогорова-Смирнова).
На рис. 1 представлены гистограммы измерений реального трафика.По статистическим критериям согласия Колмогорова-Смирнова и Андерсона-Дарлинга наибольшее приближение к гистограмме представленного реального трафика имеет распределение Берра (Burr) (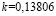
, 
, 
, 
).
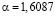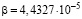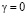Рассмотрим аппроксимацию распределения Берра (Burr) с помощью суммы экспонент. Аналитическое выражение аппроксимирующей функции при количестве узлов интерполирования n=5 имеет вид (1):
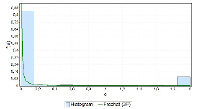
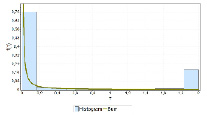
Рис. 1. Гистограммы длительности поступления пакетов трафика τi и длительности обслуживания пакетов трафика ξi
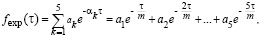(1)
где m – параметр, который определяется экспериментально для каждой аппроксимируемой функции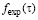 
, в нашем случае 
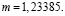Значение погрешности приближенного значения 
.
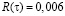Аналогично строим гистограмму по значениям случайных величин длительности обслуживания пакетов ξj в узле мультисервисной сети (рис. 1). Согласно кривой приближения, по заданным критериям согласия, неизвестная функция плотности распределения длительности обслуживания пакетов соответствует функции плотности распределения Фреше (Frechet) (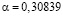
, 
, 
.
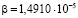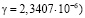Аналитическое выражение аппроксимирующей функции имеет вид 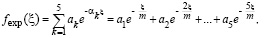(2):
(2)
где m – параметр, который определяется экспериментально для каждой аппроксимируемой функции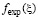 
, в нашем случае 
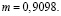Значение погрешности приближенного значения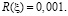 
Полученная неизвестная функция плотности распределения в дальнейшем используется для анализа выходных характеристик СМО G/G/1.
С помощью алгоритма, описанному в [6], находим функцию времени ожидания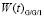 
(рис. 2).
Соответственно, согласно [6, 7], находим среднее время ожидания пакета в очереди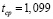 
. Определим среднее число пакетов в системе по соотношению 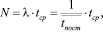(3)
(3)
где l – интенсивность поступления пакетов в систему; 
– среднее значение интервала времени между поступлениями очередных пакетов (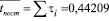
).
Следовательно,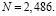 
Для сравнения полученных значений приведем результаты вычисления функции распределения времени ожидания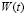 
для классических СМО М/М/1, Er/M/1.
Функции распределения времени ожидания для системы М/М/1 (при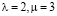 
) можем определить (4) из [1]:
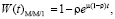(4)
Аналогично определим для системы Er/M/1 (при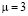 
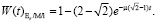) (5):
(5)
На рис. 3 и 4 представлены графики функции распределения времени ожидания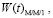 
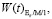
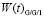и графики функции плотности времени ожидания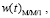 
.
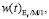
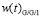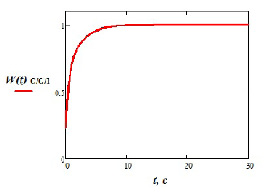
Рис. 2. График функции распределения времени ожидания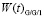 
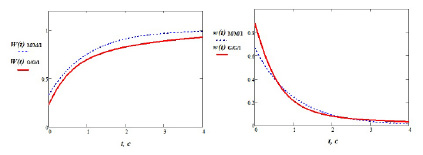
Рис. 3. Графики функций распределения времени ожидания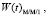 
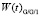и плотности распределения времени ожидания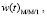 
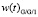
На рис. 3 показано сравнение функций распределения времени ожидания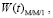 
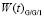и плотности распределения времени ожидания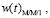 
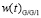, полученных классическим спектральным методом для СМО М/М/1 и с помощью аппроксимации суммой затухающих экспонент для СМО G/G/1.
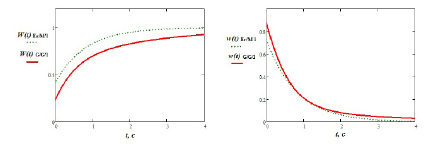
Рис. 4. Графики функций распределения времени ожидания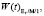 
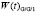и плотности распределения времени ожидания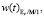 
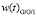
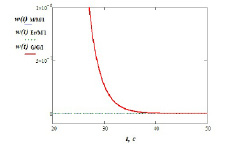
Рис. 5. Графики функций плотности распределения времени ожидания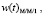 
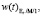
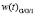
Аналогично на рис. 4 представлено сравнение функций распределения времени ожидания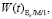 
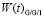и плотности распределения времени ожидания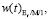 
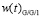, полученных классическим спектральным методом для СМО Er/M/1 и с помощью аппроксимации суммой затухающих экспонент для СМО G/G/1.
Выводы
Сравнение графиков (рис. 3, 4) показывает, насколько оптимистичные результаты дают классические формулы для расчета характеристик СМО М/М/1, G/M/1 по сравнению с рассмотренным частным случаем СМО G/G/1.
Из рис. 5 видно, что экспоненциальные распределения не учитывают «долгий», затухающий хвост функции плотности распределения, который характеризует реальный поступающий трафик сети. Поэтому исследование выходных характеристик трафика реальной мультисервисной сети, представленного в виде СМО G/G/1 представляет интерес. Таким образом, с помощью спектрального метода есть возможность определить параметры узла сети: интенсивности поступления и обслуживания пакетов, среднее времени ожидания пакетов в очереди и среднее число пакетов в системе.
Библиографическая ссылка
Киреева Н.В., Чупахина Л.Р. СРАВНЕНИЕ ХАРАКТЕРИСТИК СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ M/M/1 И G/G/1 СПЕКТРАЛЬНЫМ МЕТОДОМ // Современные наукоемкие технологии. – 2014. – № 12-2. – С. 160-164;URL: https://top-technologies.ru/ru/article/view?id=34953 (дата обращения: 03.12.2024).