Построение специализированных вычислительных устройств, реализующих цифровую обработку сигналов (ЦОС) в реальном масштабе времени, возможно за счет применения параллельных модулярных кодов. Такие коды позволяют эффективно реализовать операции сложения, умножения и вычитания по модулю. Так как основными операциями алгоритмов ЦОС являются именно эти операции, то использование алгебраических систем, обладающих свойством кольца и поля, позволит обеспечить высокую скорость обработки сигналов [1–5]. Кроме того модулярные коды позволяют обнаруживать и корректировать ошибки, которые возникают из-за отказов или сбоев в процессе функционирования специализированных процессоров ЦОС.
В полиномиальной системе классов вычетов в качестве основания системы используется минимальные многочлены pi(z), i=1,2,…,n, определенные в расширенных полях Галуа GF(2ν). Тогда любой полином 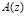 , удовлетворяющий условию
, удовлетворяющий условию
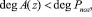 (1)
(1)
где 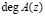 – степень полинома A(z);
– степень полинома A(z); 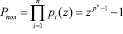 – полный диапазон, можно представить в виде n-мерного вектора
– полный диапазон, можно представить в виде n-мерного вектора
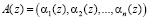 , (2)
, (2)
где
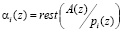 ,
, 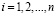 .
.
Так как сравнения по одному и тому же модулю можно почленно складывать, вычитать и умножать, то для суммы, разности и произведения двух полиномов 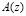 и
и 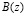 , имеющих соответственно модулярные коды
, имеющих соответственно модулярные коды 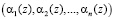 и
и 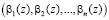 справедливы соотношения:
справедливы соотношения:
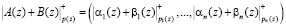 , (3)
, (3)
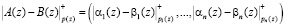 , (4)
, (4)
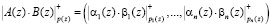 . (5)
. (5)
Таким образом, выполнение операций над операндами в ПСКВ производятся независимо по каждому из модулей 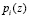 , что указывает на параллелизм данной алгебраической системы.
, что указывает на параллелизм данной алгебраической системы.
Кроме того, особенность ПСКВ состоит еще и в том, что независимость обработки информации по основаниям ПСКВ позволяет не только повысить скорость и точность обработки, но так же и обеспечить обнаружение и коррекцию ошибок в процессе функционирования вычислительного устройства класса вычетов. Если на диапазон возможного изменения кодируемого множества полиномов наложить ограничения, то есть выбрать 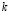 из
из 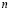 оснований ПСКВ (
оснований ПСКВ (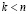 ), то это позволит осуществить разбиение полного диапазона
), то это позволит осуществить разбиение полного диапазона
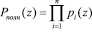
расширенного поля Галуа 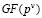 на два непересекающихся подмножества. Первое подмножество называется рабочим диапазоном и определяется выражением
на два непересекающихся подмножества. Первое подмножество называется рабочим диапазоном и определяется выражением
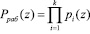 , (6)
, (6)
Многочлен 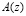 с коэффициентами из поля
с коэффициентами из поля 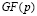 будет считаться разрешенным в том и только том случае, если он является элементом нулевого интервала полного диапазона
будет считаться разрешенным в том и только том случае, если он является элементом нулевого интервала полного диапазона 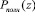 , то есть принадлежит рабочему диапазону
, то есть принадлежит рабочему диапазону 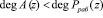 .
.
Для определения местоположения и глубины ошибки в кодах ПСКВ используются позиционные характеристики (ПХ) [6-10]. Благодаря этим алгоритмам вычисления (ПХ) можно определить местоположение полинома 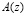 относительно рабочего диапазона. А это позволяет однозначно определить, является ли кодовая комбинация ПСКВ
относительно рабочего диапазона. А это позволяет однозначно определить, является ли кодовая комбинация ПСКВ 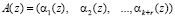 разрешенной, или содержит ошибочные символы. Особое место среди позиционных характеристик модулярного кода занимают коэффициенты обобщенной полиадической системы (ОПС).
разрешенной, или содержит ошибочные символы. Особое место среди позиционных характеристик модулярного кода занимают коэффициенты обобщенной полиадической системы (ОПС).
В [10] представлен алгоритм вычисления коэффициентов обобщенной полиадической системы. для организации перевода из модулярного кода ПСКВ в обобщенную полиадическую систему, в которой используется 5 неприводимых полиномов p1(z)=z+1, p2(z)=z2+z+1, p3(z)=z4+z3+z2+z+1, p4(z)=z4+z3+1, p5(z)=z4+z+1, достаточно использовать двухслойную нейронную сеть.
Произведем разработку нейросетевой реализации данного алгоритма. Если положить, что первые три основания являются информационными, т.е. k = 3, то рабочий диапазон будет определяться согласно (6) и равен
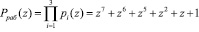 .
.
Оставшиеся два основания p4(z)=z4+z3+1 и p5(z)=z4+z+1, будем считать контрольными модулями, с помощью которых будет производиться поиск и коррекция ошибок, возникающих в кодах ПСКВ.
В этом случае, любой полином, представленный в коде ПСКВ, чья степень будет меньше семи, т.е. 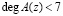 , является разрешенным, а его кодовая комбинация не содержит ошибки. В противном случае – кодовая комбинация содержит ошибки.
, является разрешенным, а его кодовая комбинация не содержит ошибки. В противном случае – кодовая комбинация содержит ошибки.
Коэффициенты обобщенной полиадической системы позволяют осуществить поиск и коррекцию ошибок в кодах ПСКВ. для данного примера полином A(z) можно представить в обобщенной полиадической системе как
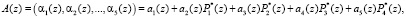 (8)
(8)
где
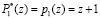 ;
; 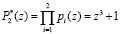 ;
;
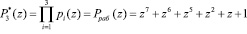 ;
;
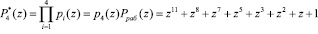 .
.
Ортогональные базисы такой системы равны:
B1(z)=z14+zl3+zl2+zll+zl0+z9+z8+z7+z6+z5+z4+z3+z2+z+1;
B2(z)=z14+z13+z11+z10+z8+z7+z 5+z4+z2+z;
B3(z)=zl4+zl3+zl2+zll+z 9+z8+z7+z6+z4+zз+z2+z;
B4(z)=z14+z13+z12+z11+z9+z7+z6+z3;
B5(z)=zl2+z9+z8+z6 +z4+z3+z2+z.
Представим ортогональные базисы в виде коэффициентов ОПС
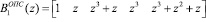 ;
;
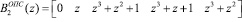 ;
;
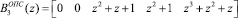 ;
;
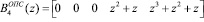 ;
;
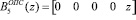 .
.
Согласно Китайской теореме об остатках полином A(z) определяется
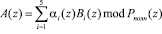 , (9)
, (9)
где 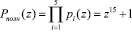 – полный диапазон ПСКВ.
– полный диапазон ПСКВ.
Если в качестве ортогональных базисов Bi(z) взять их представления в ОПС, то при умножении остатков 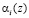 на последние, можно получить коэффициенты ОПС
на последние, можно получить коэффициенты ОПС
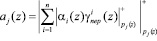 , (10)
, (10)
где 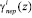 – коэффициенты ОПС i-го ортогонального базиса с учетом переполнения (i–1)-го основания.
– коэффициенты ОПС i-го ортогонального базиса с учетом переполнения (i–1)-го основания.
При этом умножение вычетов на соответствующие коэффициенты 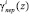 осуществляется помодульно и поразрядно, при этом учитывается превышение модуля рi(z) как перенос в старший коэффициент ОПС
осуществляется помодульно и поразрядно, при этом учитывается превышение модуля рi(z) как перенос в старший коэффициент ОПС 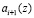 .
.
Из выражения (8) наглядно видно, что если полином A(z), представленный в ПСКВ, не содержит ошибки, то его степень не превысит степень рабочего диапазона. Следовательно, значения старших коэффициентов ОПС должны равняться нулю, т.е. a4(z) = 0 и a5(z) = 0.
Если полином A*(z), представленный в ПСКВ, содержит ошибку, то справедливо
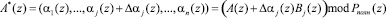 , (11)
, (11)
где Δαj(z) – глубина ошибки по j-му основанию ПСКВ.
В результате этого результат ошибочного кода A*(z) при переводе в позиционный код окажется за пределами рабочего диапазона Рраб(z). При этом по величине значений старших коэффициентов ОПС можно однозначно определить местоположение и глубину ошибки. В ходе проведенных исследований была определена связь старших коэффициентов ОПС с глубиной и местоположением ошибки в коде ПСКВ. В табл. 1 приведены эти соотношения.
Анализ таблицы показывает, что при использовании 2 контрольных оснований избыточный код ПСКВ может исправить все однократные ошибки.
Чтобы осуществлять коррекцию ошибок в комбинации кода ПСКВ, была разработана четырехслойная нейронная сеть, которая представлена на рисунке.
Таблица 1
Зависимость значений коэффициентов ОПС от местоположения и глубины ошибки для поля 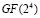
|
Величина ошибки |
Коэффициенты ОПС |
|
|
a4 (z) |
a5 (z) |
|
|
Δa1=1 |
z3 |
z3 + z2 + z |
|
Δa2=1 |
z3 + z + 1 |
z3 + z2 |
|
Δa2=z |
z3 + z2 +z |
z3 + z |
|
Δa3=1 |
z2 + 1 |
z3 + z2+ z |
|
Δa3=z |
z3 + z |
z3 + z2 + z + 1 |
|
Δa3=z2 |
z3 + z2 |
z3 + z2 |
|
Δa3=z3 |
1 |
z3 + z |
|
Δa4=1 |
z2 + z |
z3 + z2 + z |
|
Δa4=z |
z3 + z2 |
z3 + z2 + z + 1 |
|
Δa4=z2 |
1 |
z3 + z2 |
|
Δa4=z3 |
z |
z3 + z + 1 |
|
Δa5=1 |
0 |
z |
|
Δa5=z |
0 |
z2 |
|
Δa5=z2 |
0 |
z3 |
|
Δa5=z3 |
0 |
z+1 |
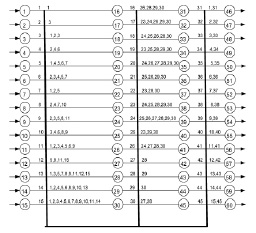
Нейронная сеть для коррекции кодов ПСКВ
Каждый слой содержит по 15 нейронов. Входной слой состоит из 15 нейронов, распределенных в соответствии с размерностью разрядных сеток модулей -1-2-4-4-4. Данные нейроны осуществляют разветвление входного вектора 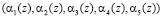 , представленного в двоичной форме. Причем нейрон 1 предназначен для распределения нулевого разряда
, представленного в двоичной форме. Причем нейрон 1 предназначен для распределения нулевого разряда 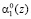 первого основания. Нейроны 2, 3 предназначены для распределения нулевого
первого основания. Нейроны 2, 3 предназначены для распределения нулевого 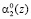 и первого
и первого 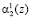 разрядов второго основания соответственно. Нейроны 4-7 используются для приема и распределения
разрядов второго основания соответственно. Нейроны 4-7 используются для приема и распределения 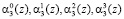 разрядов третьего основания соответственно. для перераспределения разрядов
разрядов третьего основания соответственно. для перераспределения разрядов 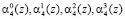 четвертого основания p4(z) используются нейроны 8, 9, 10, 11 соответственно. Нейроны 12, 13, 14, 15 применяются для приема разрядов
четвертого основания p4(z) используются нейроны 8, 9, 10, 11 соответственно. Нейроны 12, 13, 14, 15 применяются для приема разрядов 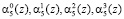 пятого основания p5(z) соответственно.
пятого основания p5(z) соответственно.
Второй слой нейронной сети содержит также 15 нейронов, распределенных в соответствии с размерностью разрядных сеток коэффициентов (аi(z), i=1,2,3,4,5) ОПС -1-2-4-4-4. Нейроны 16-30 второго слоя выполняют базовую операцию суммирования по модулю два значений разрядов, поступающих с выходов соответствующих нейронов первого слоя, и реализуют выражение (10). Синаптические веса связей равны единице.
Выход нейрона 16 соответствует нулевому разряду первого коэффициента ОПС а1(z). Нейроны 17, 18 осуществляют вычисление нулевого и первого 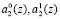 разрядов второго коэффициента ОПС соответственно. Нейроны 19, 20, 21, 22 осуществляют вычисление нулевого, первого, второго и третьего разрядов
разрядов второго коэффициента ОПС соответственно. Нейроны 19, 20, 21, 22 осуществляют вычисление нулевого, первого, второго и третьего разрядов 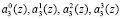 третьего коэффициента ОПС а3(z) соответственно. Нейроны 23, 24, 25, 26 осуществляют вычисление нулевого, первого, второго и третьего разрядов
третьего коэффициента ОПС а3(z) соответственно. Нейроны 23, 24, 25, 26 осуществляют вычисление нулевого, первого, второго и третьего разрядов 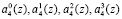 четвертого коэффициента ОПС а4(z) соответственно. Нейроны 27, 28, 29, 30 осуществляют вычисление нулевого, первого, второго и третьего разрядов
четвертого коэффициента ОПС а4(z) соответственно. Нейроны 27, 28, 29, 30 осуществляют вычисление нулевого, первого, второго и третьего разрядов 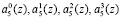 пятого коэффициента ОПС а5(z) соответственно.
пятого коэффициента ОПС а5(z) соответственно.
Третий слой нейронной сети содержит также 15 нейронов. Нейроны 31–45 третьего слоя выполняют базовую операцию логического умножения (логическое «И») значений разрядов, поступающих с выходов соответствующих нейронов второго слоя. Синаптические веса связей равны единице.
Четвертый слой сети содержит также 15 нейронов. Нейроны 46–60 четвертого слоя выполняют базовую операцию суммирование по модулю два значений разрядов, поступающих с выходов соответствующих нейронов первого и третьего слоев сети, что позволяет откорректировать ошибку в кодовой комбинации ПСКВ. Синаптические веса связей равны единице. Так вход 46 нейрона четвертого слоя соединен с выходом 1 нейрона первого слоя и с выходом 31 нейрона третьего слоев нейронной сети. Выходы нейронов 46-60 второго слоя являются выходами нейронной сети.
Пусть на вход нейронной сети подается полином 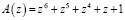 , который принадлежит рабочему диапазону
, который принадлежит рабочему диапазону 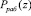 . Тогда его код в ПСКВ имеет вид A(z)=(1, z+1, z3+z2+z+1, z3+z2+z, z3+z), и при этом он не содержит ошибки. Воспользуемся выражением (10) и произведем вычисление коэффициентов ОПС. В результате вычислений были получены следующие значения
. Тогда его код в ПСКВ имеет вид A(z)=(1, z+1, z3+z2+z+1, z3+z2+z, z3+z), и при этом он не содержит ошибки. Воспользуемся выражением (10) и произведем вычисление коэффициентов ОПС. В результате вычислений были получены следующие значения
a1(z)=1, a2(z)=z+1, a3(z)=z3+z2+z+1, а4(z)=0, a5(z)=0.
Это свидетельствует о том, что данная кодовая комбинация, представленная в ПСКВ, не содержит ошибки. Работу первого и второго слоев нейронной сети рассмотрим с использованием табл. 2. и произведем вычисление коэффициентов ОПС.
Таким образом, полином A(z)=(1, z+1, z3+z2+z+1, z3+z2+z, z3+z) представляется в ОПС в следующем виде a1(z)=1, a2(z)=z+1, a3(z)=z3+z2+z+1, а4(z)=0, a5(z)=0. Так как старшие коэффициенты ОПС равны нулю, то это свидетельствуют, что кодовая комбинация ПСКВ не содержит ошибку, и ее не надо корректировать. В этом случае с выходов нейронов 23–26 и 27–30, которые соответствуют двоичному представлению коэффициентов а4(z) и a5(z), снимается нулевой результат. В соответствии с этим на выходах нейронов 31–45 третьего слоя, выполняющих операцию логического умножения, будет также нуль. Это значение поступает на входы нейронов 46–60 четвертого, которые суммируют эти значения с остатками 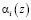 , подаваемых с выходов нейронов 1–15 первого слоя. В этом случае кодовая комбинация ПСКВ не изменяется.
, подаваемых с выходов нейронов 1–15 первого слоя. В этом случае кодовая комбинация ПСКВ не изменяется.
Таблица 2
Вычисление коэффициентов ОПС
|
Основания pi(z) |
z+1 |
z2+z+1 |
p3=z4+z3+z2+z+1 |
p4=z4+z3+1 |
p5=z4+z+1 |
|||||||||||
|
Разряды pi(z) |
1 |
1 |
z |
1 |
z |
z2 |
z3 |
1 |
z |
z2 |
z3 |
1 |
z |
z2 |
z3 |
|
|
№ нейронов |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
|
p1(z)= z+1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||||
|
p2(z)= z2+z+1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||||
|
z |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||||||||
|
p3=z4+z3+z2+z+1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||||
|
z |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||||
|
z2 |
1 |
1 |
1 |
1 |
1 |
1 |
||||||||||
|
z3 |
1 |
1 |
1 |
1 |
1 |
|||||||||||
|
p4(z)=z4+z3+1 |
z |
1 |
1 |
1 |
1 |
1 |
1 |
|||||||||
|
z2 |
1 |
1 |
1 |
|||||||||||||
|
z3 |
1 |
1 |
1 |
1 |
||||||||||||
|
p5(z)=z4+z+1 |
z |
1 |
||||||||||||||
|
z3 |
1 |
1 |
||||||||||||||
|
Коэффициенты ОПС ai(z) |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Пусть ошибка произошла в первом остатке, т.е. 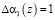 . В результате этого на вход нейронной сети поступает код
. В результате этого на вход нейронной сети поступает код
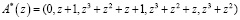 ,
,
на выходах нейронов 16–30 второго слоя получатся значения коэффициентов ОПС.
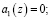
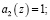
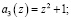
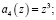
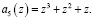
Так как значения старших коэффициентов ОПС 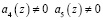 , то это свидетельствует о том, что кодовая комбинация содержит ошибку.
, то это свидетельствует о том, что кодовая комбинация содержит ошибку.
В соответствии с полученными значениями 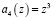 и
и 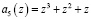 единичный сигнал будет на выходе 26, 28, 29 и 30 нейронов второго слоя. Этот сигнал с выхода нейронов 26, 28, 29, 30 поступает на входы 31 нейрона третьего слоя. В результате этого только на выходе 31 нейрона третьего слоя появляется единичный сигнал, который поступает на второй вход 46 нейрона. Этот корректирующий сигнал
единичный сигнал будет на выходе 26, 28, 29 и 30 нейронов второго слоя. Этот сигнал с выхода нейронов 26, 28, 29, 30 поступает на входы 31 нейрона третьего слоя. В результате этого только на выходе 31 нейрона третьего слоя появляется единичный сигнал, который поступает на второй вход 46 нейрона. Этот корректирующий сигнал 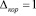 складывается с выходным сигналом 1 нейрона первого слоя
складывается с выходным сигналом 1 нейрона первого слоя 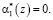
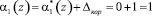 .
.
В результате работы нейронной сети ошибка в кодовой комбинации ПСКВ исправлена
Aисправ(z) = (1, z+1, z3+z2+z+1, z3+z2+z, z3+z).
Выводы
Современные модулярные коды позволяют повысить скорость выполнения алгоритмов ЦОС за счет параллельной обработки малоразрядных остатков. Кроме того эти коды также позволяют осуществлять поиск и коррекцию ошибок, которые могут возникать в процессе функционирования непозиционного спецпроцессора. В работе приведен пример реализации алгоритма поиска и коррекции ошибки, который использует расширение системы оснований. В статье приведена структура устройства коррекции модулярного кода, использующего разработанный алгоритм.
Библиографическая ссылка
Дунин А.В., Калмыков М.И., Рассветаев В.В., Лобойкин В.В. НЕЙРОСЕТЕВАЯ РЕАЛИЗАЦИЯ АЛГОРИТМА КОРРЕКЦИЯ ОШИБОК В МОДУЛЯРНОМ КОДЕ НА ОСНОВЕ КОЭФФИЦИЕНТОВ ОБОБЩЕННОЙ ПОЛИАДИЧЕСКОЙ СИСТЕМЫ // Современные наукоемкие технологии. 2014. № 12-2. С. 145-151;URL: https://top-technologies.ru/ru/article/view?id=34950 (дата обращения: 13.03.2026).



