Вибрационные технологические процессы получили широкое распространение в производственных системах, относящихся к различным отраслям техники [1, 2]. Вибрации активно используются в технологиях обработки деталей, таких как вибрационное резание материалов, виброгалтовка, вибрационное упрочнение и др. [3].
Задача исследования заключается в разработке метода построения математических моделей динамических процессов взаимодействия обрабатываемых деталей и сыпучей среды, адекватно отражающих особенность технологического процесса как со стороны формирования необходимой структуры вибрационного поля, так и учета возникающих особенностей в технологическом процессе виброупрочнения поверхности детали путем периодического виброударного контактирования с сыпучей рабочей средой.
Методологические основы оценки динамического контакта для твердых тел с одной точкой контакта для режимов с кратным периодом подбрасывания
Разработаны подходы к построению математических моделей, отражающих особенности динамических взаимодействий, характерных для технологических процессов вибрационного упрочнения. Технологические эффекты достигаются в периодических виброударных контактах рабочей среды из мелких стальных шариков и вибрирующей рабочей поверхности обрабатываемой детали. Рассматриваемые модели предполагают возможность реализации фазы свободного подлета.
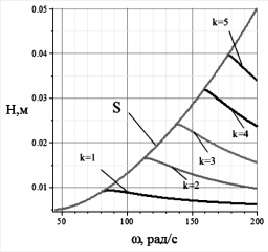
Рис. 1. Высота подлета для точек второго и третьего порядка при реализации режима подбрасывания в одно касание
На основе теоретических оценок разрабатываются представления о требованиях к особенностям движения отдельных частиц, формирующих рациональные параметры процесса вибрационного упрочнения. Для оценки особенностей формирования свободного подлета используется функция зазора, которая представляет собой теоретический аппарат для оценки возможностей реализации различных режимов непрерывного подбрасывания [4]. На рис. 1 представлены характеристики режимов подбрасывания элементов рабочей среды с учетом дифференциального критерия отрыва с использованием функции зазора.
В соответствии с рис. 1 графиком S представлены величины высот подлета материальной частицы с отрывом в точке третьего порядка в зависимости от частоты колебания поверхности. Кривые k = 1, ..., k = 5 представляют величины высот подлета частиц с отрывом в точках второго порядка кратности k.
Метод оценки условий сохранения динамического контакта для составного твердого тела с учетом неудерживающего характера связей
Рассматриваются математические модели твердых тел с использованием упругих связей при вибрациях опорной поверхности и возможностью нарушения контакта. На рис. 2 представлен пример математической модели, в которой условие нарушение контакта определяется параметрами массоинерционных и упругих связей.
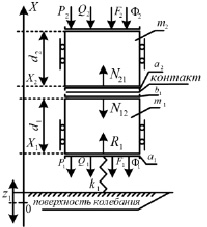
Рис. 2. Составное твердое тело на упругом колеблющемся основании
На рис. 2 плоскость Z1 представляет собою опорную поверхность колебания; Pi – силы вязкого трения; Qi – силы тяжести; Fi – постоянные силы; N12, N21 полные контактные реакции; a2, b1 – контактные поверхности. Два элемента составного твердого тела с массами m1 и m2 находятся в неудерживающем контакте.
Получены граничные условия совместных движений, при которых вибрация основания не приводит к нарушению контакта. Вводится понятие о полной и динамической реакциях, предлагается методика расчетов. Получены аналитические условия, определяющие контактные движения. В зависимости от параметров систем условие контактного движения принимает вид
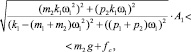 (*)
(*)
где ki – жесткости элементов; pi – коэффициенты вязкого трения; fc – постоянная сила; ω1 и A1 – частота и амплитуда колебаний опорной поверхности.
Неравенство (*) представляет аналитическую зависимость между параметрами системы, обеспечивающими контактное движение составного твердого тела в установившемся режиме в виде амплитудно-частотной области контакта [5–7].
Методы параметрического регулирования динамического контакта с учетом неудерживающего характера связей. Измерительные устройства для фиксации условий вибрационного взаимодействия при неудерживающих связях. Некоторые приложения
На основе аналитических условий контактного колебания составных твердых тел предложены подходы к регулированию контактного взаимодействия. Для регистрации различных состояний вибрационных взаимодействий разработан опытный датчик определения граничных режимов взаимодействия тел в вибрационных системах [8]. Принципиальная схема датчика приведена на рис. 3.
В соответствии с рис. 3 представлены следующие составляющие: поверхность вибростола – 5; цилиндрический корпус датчика – 1; инерционный элемент рабочей среды – 2; пьезоэлектрический элемент – 3; крепежный элемент – 4; токовыводы – 6.
Представленные исследования позволяют разрабатывать обобщенные подходы к задачам определения контактных реакций в твердых телах при статических и динамических нагрузках с учетом неудерживающих связей. Вместе с тем сформированный теоретический базис выступает основой для формирования концепции взаимодействия слоя рабочей среды с обрабатываемой поверхностью.
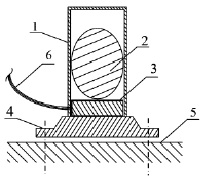
Рис. 3. Принципиальная схема датчика
Заключение
На основе исследований могут быть сделаны следующие выводы.
1. Разработан обобщенный подход для задач динамического синтеза вибрационных технологий, реализуемых в режимах непрерывного подбрасывания. Основой подхода является введение понятия о функции зазора, позволяющей обосновать построение траекторий движений материальных частиц в соответствии с определенными критериями, отражающими свойства траекторий движения материальных частиц во взаимодействии с вибрирующей поверхностью.
2. Разработан метод построения математических моделей и определения условий беззазорного движения системы элементов или твердых тел, состоящих из нескольких соприкасающихся частей. Метод представляет собою совокупность последовательных действий по составлению расчетной схемы механической колебательной системы с выделением элементов, образующих между собой неудерживающие связи; определение статических и динамических реакций; преобразование Лапласа системы дифференциальных уравнения движения исходной механической системы; составление неравенства на основе амплитудно-частотных характеристик; определение функции критической амплитуды для простого контакта (минимума критических амплитуд для сложного контакта) и аналитико-графическое представление функции критической амплитуды и параметров, удовлетворяющих составленному неравенству, определяющего условия движения исходной системы без возникновения зазоров в режиме установившихся колебаний.
3. На основе аналитических исследований и численного моделирования установлено, что зависимость контактного взаимодействия от вязкого трения, жесткости упругих элементов и масс фрагментов твердых тел определяется частотой колебания опорных поверхностей. При различных частотах колебаний изменение обобщенных параметров, характеризующих вязкость, жесткость элементов и массу фрагментов системы, может способствовать контакту или приводить к нарушению условий контакта. Установлено также, что в зависимости от частоты колебания существуют диапазоны масс нарушения контактного взаимодействия. Влияние жесткости на контактное взаимодействие определяется частотой колебания опорных поверхностей.
Библиографическая ссылка
Елисеев А.В., Копылов Ю.Р. НЕКОТОРЫЕ ВОПРОСЫ ДИНАМИКИ ВИБРАЦИОННОГО ВЗАИМОДЕЙСТВИЯ СЫПУЧЕЙ СРЕДЫ И ПОВЕРХНОСТИ С УЧЕТОМ НЕУДЕРЖИВАЮЩИХ СВЯЗЕЙ // Современные наукоемкие технологии. 2015. № 3. С. 28-31;URL: https://top-technologies.ru/ru/article/view?id=34918 (дата обращения: 05.03.2026).



