Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Акатьев В.А. 1 Нигметов Г.М. 2 Нигметов Т.Г. 1

---

1 ФГБОУ ВПО «Российский государственный социальный университет»

2 ФГБУ «Всероссийский научно-исследовательский институт по проблемам гражданской обороны и чрезвычайных ситуаций»

Проведен анализ влияния степени армирования железобетонных балок на их амплитудно-частотные характеристики. При этом экспериментальным исследованиям были подвергнуты армированные и неармированные балки, имеющие одинаковые поперечные сечения и длины. Одна группа образцов была изготовлена из бетона марки 150, другая группа – из бетона марки 300. Экспериментальные результаты были сопоставлены с результатами расчетов по действующим методикам. Выявлена значительная разница между экспериментальными и расчетными показателями. Степень снижения периода собственных колебаний балки с увеличением степени армирования по данным эксперимента значительно выше, чем по расчетным оценкам с использованием методик.

Статья в формате PDF

2720 KB

поперечные собственные колебания

балка

армирование

амплитудно-частотная характеристика

период колебаний балки

1. Коробко В.И., Коробко А.В. Контроль качества строительных конструкций: Виброакустические технологии. – М.: Ассоциация строительных вузов, 2003. – 288 с.

2. Пановко Я.Г. Основы прикладной теории колебаний и удара. – 5-е изд. – М.: Либроком, 2010. – 274 с.

3. Тимошенко С.П. Колебания в инженерном деле: пер. с англ. Я.Г. Пановко. – 2-е изд., стереотип. – М.: Комкнига, 2006. – 440 с.

4. СП 52-101-2003. Бетонные и железобетонные конструкции без предварительного напряжения арматуры.

В существующей научно-технической литературе и методических документах должным образом не нашли отражение вопросы учета влияния армирования железобетонных конструкций на их жесткость и, как следствие, на их колебательную способность. Результаты анализа показывают, что при одинаковых длинах, сечениях и прочностных характеристиках бетонные и железобетонные балки имеют разный частотный портрет колебаний, что говорит о влиянии армирования на динамику балок. Определение нормативного (проектного) значения периода собственных колебаний железобетонных конструкций и периода собственных колебаний при эксплуатации даёт возможность диагностировать изменение их жесткости E∙J в момент времени контроля t.

Постановка задачи исследования

Свободные колебания балки описываются известным дифференциальным уравнением [1, 2, 3]:

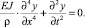(1)

Решение дифференциального уравнения (1) для балки дает следующую зависимость для периода собственных колебаний:

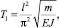(2)

где l – длина балки, м; m – масса погонного метра балки, кг/м; Е – модуль упругости, Н/м2; J – момент инерции сечения балки, м4.

Требуется решить следующие задачи. Вначале определить расчетные значения периодов собственных колебаний балок с учетом их армирования по формуле (2), затем значения тех же параметров (отдельно для армированных и неармированных балок) получить в результате экспериментального исследования. На конечном этапе полученные результаты сопоставить между собой.

Характеристика образцов, использованных для исследования

Для анализа колебаний были отобраны бетонные (неармированные) и железобетонные образцы (2 бетонные и 2 железобетонные балки) длиной по 1 м, изготовленные из бетона марки М-150 и М-300 и имеющие прямоугольное поперечное сечение шириной 80 мм и высотой 140 мм. Железобетонные балки по нижней зоне сечения армированы двумя стальными стержнями диаметром 12 мм, защитный слой бетона равен 10 мм.

Теоретическая оценка влияния армирования и прочности на динамические колебания железобетонных балок

Момент инерции прямоугольного сечения бетонной балки относительно центральной оси вычислим по известной формуле:

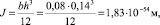
где b – ширина сечения балки, м; h – высота сечения балки, м.

Момент инерции сечения железобетонной балки (Jприв) определим как приведенный момент инерции с армированием – с учетом всей площади сечения бетонной балки и площадей сечения арматуры с учетом коэффициентов приведения арматуры к бетону [4]:

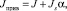(3)

где Js – момент инерции площади сечения растянутой арматуры в нижней зоне относительно центра тяжести приведенного поперечного сечения определяется по формуле:

J_sрас = А_s∙(h_о – y_c)²; (4)

y_c – расстояние от центра тяжести сечения до наиболее растянутого волокна (y_c = 0,07 м); h_о – рабочая высота сечения балки; α – коэффициент приведения арматуры к бетону, α = Е_s/E_b.

Для марок бетона М-150 и М-300 и стальной арматуры сформируем исходные данные для последующего расчета моментов инерции:

модуль упругости, Е, МПа:

Е₁₅₀ = 21∙10³, Е₃₀₀ = 30∙10³, Еs = 2∙10⁵;

плотность, ρ, кг/м3:

ρ₁₅₀ = 2460, ρ₃₀₀ = 2389, ρ_s = 7850;

коэффициент приведения арматуры к бетону:

α150 = 9, 52, α300 = 6, 67.

С учетом приведенных исходных выполним вычисления моментов инерции сечения железобетонных балок:

J_s150 = J + J_sрас∙α = 1,83∙10^–5 + 0,000000463∙2∙9,52 = 2,7∙10^–5;

J_s300 = J + J_sрас∙α = 1,83∙10^–5 + 0,000000463∙2∙ 6,67 = 2,45∙10^–5.

Найдем отношения моментов инерции для сечений балок с армированием и без армирования:

J_s150/J = 2,7/1,83 = 1,475;

J_s150/J = 2,45/1,83 = 1,34.

Тогда можно вычислить отношение периодов собственных колебаний балок с армированием и без армирования для бетона марок 150 и 300:

Т _1,150s/Т _1,150 = 0,82;

Т _1,300s/Т _1,300 = 0,86.

Экспериментальные измерения динамических колебаний балок

Эксперименты выполнялись с помощью комплексов для динамических испытаний «Струна-Стрела» и «Толкун-1» с применением пьезокерамических акселерометров типа А1638 в частотном диапазоне от 0,1 до 400 Гц. Общий вид на образцы и приборы контроля, подготовленные к эксперименту, представлены на рис. 1.

Спектры колебаний балок представлены на рис. 2 и 3.

Из анализа спектров колебаний балок из бетона марки М-300 можно определить экспериментальные значения периодов собственных колебаний (T_жб = 0,012 с – для армированной; T_б = 0,042 с – для неармированной) и оценить их отношения (Т_б/Т_жб = 3,50). Значения периодов собственных колебаний балок (с армированием и без армирования) можно вычислить по формулам, изложенных в методиках [1–4].

Результаты сравнения периодов собственных колебаний балок с армированием и без армирования, полученные в результате вычислений, показывают, что указанные периоды должны отличаться в 1,22–1,16 раз, тогда как результаты экспериментальных данных показывают, что периоды колебаний для исследуемых балок отличаются в 2,86–3,50 раза (таблица).

Рис. 1. Динамические испытания бетонных балок

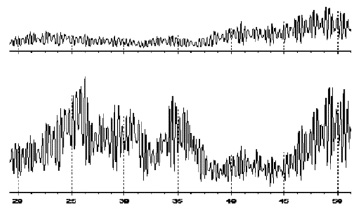
Рис. 2. Спектры колебаний в частотном диапазоне от 20 до 50 Гц: сверху – балка из бетона марки 300 с армированием; снизу – балка из бетона марки 300 без армирования

Отношение периодов собственных колебаний балок без армирования Т_б и с армированием Т_жб

В литературе [1] приводятся математические выражения для оценки периодов собственных колебаний, с помощью которых можно определить влияние степени армирования, в частности, при расположении арматуры в нижней зоне период колебаний балки должен возрасти максимум в 2,24 раза, но это не соответствует экспериментальным значениям периодов собственных колебаний балки.

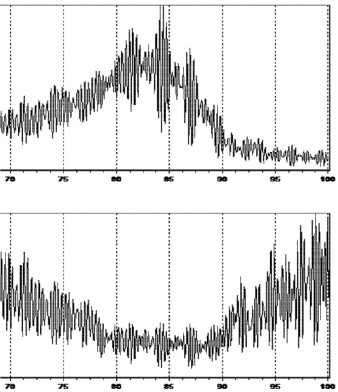
Рис. 3. Спектры колебаний балок из бетона марки 300 в частотном диапазоне от 70 до 100 Гц: сверху – для балки с армированием; снизу – для балки без армирования

Следует иметь в виду, что период собственных колебаний железобетонной балки в процессе длительной эксплуатации меняется, что позволяет судить о степени её износа.

Для оценки степени износа железобетонной конструкции достаточно сравнить расчетные и истинные экспериментально полученные значения периодов собственных колебаний на момент времени t. Степень износа конструктивной системы может быть определена по следующей зависимости:

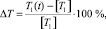(5)

где [Т₁] – нормативное значение периода собственных колебаний; Т₁(t) – период собственных колебаний в момент времени t.

Для определения нормативного значения периода собственных колебаний конструктивной системы с армированием необходимы новые методики учета влияния армирования на динамику железобетонных конструкций. Так как в настоящее время отсутствуют методики учета влияния армирования на динамику железобетонных конструкций, то для определения [Т₁] достаточно измерить Т₁ в момент времени t = 0, то есть для новой конструкции [Т₁] = Т1(0).

Тогда формулу (5) можно будет переписать следующим образом:

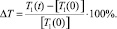(6)

При превышении периода собственных колебаний на 90 % (ΔТ ≥ 90 %) конструкция не пригодна к эксплуатации.

Выводы

При одинаковых сечениях и прочностных характеристиках бетонные и железобетонные балки имеют разный частотный спектр динамических собственных колебаний, что говорит о существенном влиянии армирования на динамику балок. Экспериментальные данные свидетельствуют о том, что существующие расчетные методики не позволяют получить объективную информацию о периодах собственных колебаний армированных балок. Расхождения расчетных данных с экспериментальными данными отличаются более чем в 2 раза. Следовательно, требуются исследования по корректировке известных расчетных зависимостей для определения динамических характеристик балок с учетом их армирования.

Библиографическая ссылка