Ввиду уменьшения размеров используемых девайсов исследование тепловых процессов на наноуровне становится все более перспективной областью науки [1, 2]. Однако физические характеристики вещества в виде тонкой пленки могут существенно отличаться от свойств этого же вещества в массивном состоянии. Знание основных закономерностей изменения свойств при переходе от массивных образцов к тонким пленкам необходимо для создания пленочных материалов с заданными свойствами.
На сегодняшний день широкое применение получило использование золота в качестве материала для тонких пленок. Оно имеет кубическую гранецентрированную решетку типа Cu с параметром решётки а=4,0781 Å. Расположение атомов в структурном типе меди соответствует кубической (трёхслойной) плотнейшей шаровой упаковке одинаковых атомов. Координационное число каждого атома – 12, координационный полиэдр – кубооктаэдр.
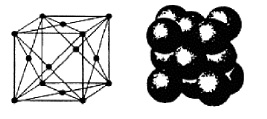
Рис. 1. Гранецентрированная кубическая (ГЦК) элементарная ячейка кристаллической решетки золота и схема упаковки атомов [1]
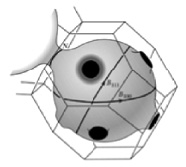
Одной из важных характеристик материала является поверхность Ферми. Она объясняет такие свойства металлов, как блеск, ковкость, электропроводимость и теплопроводность, а также отделяет заполненные электронные состояния в металлах от незаполненных при абсолютном нуле температуры [3]. Топология поверхности Ферми для меди, серебра и золота приблизительно одинаковая и представляет собой гофрированный сфероид с восьмью узкими трубками, через которые он соединяется со сфероидами соседних первых зон Бриллюена. Поверхность Ферми золота и соединение двух сфероидов золота в плоскости гексагональной грани представлена на рис. 2а, общая картина соединения нескольких ферми-сфероидов дана на рис. 2б.
 а
а  б
б
Рис. 2. Поверхность Ферми золота и зоны Бриллюена [3]
Тонкие пленки широко используются для хранения данных, кроме того, использование тонких пленок распространено и в других направлениях микроэлектроники, где используется механизм изменения размеров наночастиц с помощью тепла [1, 4]. Теплопроводность металлов подробно изучена в терминах макропараметров, однако на наноуровне могут возникать новые явления. При нанесении тонкой пленки на подложку возможны некоторые проблемы, обусловленные спецификой эффекта теплового расширения для нанокристаллических структур. На свойства пленки значительное воздействие оказывает подложка, в особенности это касается коэффициента теплового расширения. Термоупругое поведение тонких пленок является предметом исследования многих работ [5, 6].
Одним из перспективных и точных методов определения параметра элементарной ячейки является метод рентгеноструктурного анализа (РСА), который широко применяется для измерения пространственной ориентации на атомном уровне, т.к. длина волны рентгеновских лучей невелика.
Таким образом, целью данной работы является проведение экспериментального измерения коэффициента теплового расширения тонких пленок из золота на силиконовой подложке методами РСА и теоретическое обоснование полученного результата.
Материалы и методы исследования
В данном исследовании на силиконовую пластину (ориентация (100)) была нанесена золотая тонкая пленка посредством термического напыления. Покрытие из золота осаждено на предварительно нанесенный слой хрома толщиной 2,2 нм для увеличения адгезии. Толщина покрытия составила 30 нм (далее 30AuCr). Золотая пластинка толщиной 30 мм была использована в качестве исходного образца. Все слои структуры были выращены вертикально и демонстрируют преимущественную ориентацию вдоль кристаллической плоскости (111) гранецентрированной элементарной ячейки золота перпендикулярно к поверхности. Кроме того, были исследованы образцы с покрытием из наночастиц для изучения вопроса о влиянии подложки на термическое расширение пленки. Диаметр частиц пленки составил 100 нм (коммерческий коллоидный раствор от BBInternational), частицы также обладали преимущественной (111) ориентацией [3].
Для определения параметров кристаллических решеток широко используется формула, вытекающая из условия Вульфа – Брегга и устанавливающая взаимосвязь между положением рефлекса и межплоскостным расстоянием [8]:
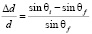 , (1)
, (1)
где d – межплоскостное расстояние, Δd – изменение межплоскостного расстояния при расширении, θi – угол, характеризующий положения исходного рефлекса, θf – угол, характеризующий положения рефлекса после нагрева. Следует отметить, что данные, полученные с использованием симметричной схемы рентгеновских съемок, будут характеризовать изменение межплоскостного расстояния именно в этом направлении, т.к. проводился анализ рефлекса от семейства плоскостей с индексами (111), параллельного поверхности образца.
Для исходного образца коэффициент линейного теплового расширения определяется формулой
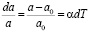 , (2)
, (2)
где a – параметр решетки золота при текущей температуре, а0 – параметр решетки золота при комнатной температуре, α – линейный коэффициент теплого расширения, dT – изменение температуры при нагреве.
Из формулы (2) видно, что линейный КТР может быть определен как угол наклона кривой, характеризующей зависимость относительного расширения кристаллической решетки от изменения температуры.
Подобный характер расширения свойственен образцам с крупным зерном, однако в некоторых работах [8] указывается, что КТР является функцией температуры и аппроксимация экспериментальных кривых, полученных в большом диапазоне температур, наиболее удачна полиномом
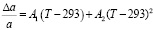 , (3)
, (3)
где а – параметр решетки при температуре 293 К, Δа – разница между параметрами решетки при текущей температуре и при 293 К, T – текущая температура, А1, А2 – коэффициенты полинома, зависящие от материала и метода определения КТР. Для измерения КТР золота методами рентгеновской дифракции они равны соответственно 1,27⋅10-5 и 4,25⋅10-9.
Как показали исследования, коэффициент теплового расширения тонкой пленки во многом зависит от материала, на который она нанесена [9]. Так, если пленка нанесена на жесткую подложку, то при тепловом расширении она испытывает сжимающие напряжения возле границы раздела, потому что подложка удерживает пленку от дальнейшего расширения. Чем тоньше пленка, тем сильнее влияние сдерживающих напряжений, генерируемых подложкой.
Существует два подхода к способу определения параметра решетки в связи с влиянием подложки, как следствие упругой деформации. Первый подход выражается в рассмотрении тепловой деформации как добавочной:
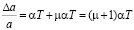 , (4)
, (4)
где µ – коэффициент Пуассона, α – коэффициент теплового расширения тонкой пленки. Однако формула (4) справедлива только для случая, когда подложка не претерпевает теплового расширения, что характерно для динамических экспериментов с лазерным нагревом. Для описания статического нагрева в температурной камере необходимо учесть влияние теплового расширения подложки:
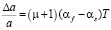 , (5)
, (5)
где αf – КТР тонкой пленки, αs – КТР подложки, µ – коэффициент Пуассона, ΔT – разница между начальной и текущей температурой.
Другой подход к описанию зависимости параметра решетки от температуры нагрева проистекает из рассмотрения напряжений в соответствии с формулой Стоуни [10], включающей анализ изменения кривизны поверхности тонкой пленки и являющейся выражением для определения двухосного напряжения. В работах [7, 9] используется подобный способ расчета деформации тонкой пленки, что приводит к выражению
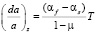 , (6)
, (6)
где αf – КТР тонкой пленки, αs – КТР подложки, µ – коэффициент Пуассона, а знак оси z для относительного расширения кристаллической решетки указывает его направление.
Учет только вертикального расширения в теоретических моделях подтверждается экспериментальными данными с разрешением по времени с помощью нагрева лазером [9].
Еще одной моделью, описывающей тепловое расширение тонкой пленки, может служить работа исследовательской группы Томсена [10], трактующая эволюцию напряжений в тонкой пленке посредством распространения акустических волн под влиянием лазера. В своих работах Томсен придерживался феноменологического описания процесса и разделял напряжение на вклад от электрического и теплового воздействия. Если сопоставить приведенные в [10] определения для изотропного теплового напряжения, можно прийти к выражению для тепловой деформации
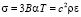 ; (7)
; (7)
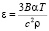 , (8)
, (8)
где B – модуль всестороннего сжатия, c – продольная скорость звука в материале, ρ – плотность материала и ε=Δa/a – деформация решетки.
Данный подход использовался в современном исследовании научной группы Матте Николя [9] в экспериментах с лазерным сверхбыстрым нагревом. Однако, как и выражение (4), формула (8) нуждается в учете расширения подложки для статического случая. Окончательно получаем
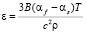 . (9)
. (9)
Условия, геометрия съемок и обработка данных. В данной работе исследование золотых тонких пленок проводилось c помощью дифрактометра Rigaku Smart Lab 9 kW Thin-Film Diffractometer (Karlsruhe Institute of technology (KIT), Institute for Photon Science and Synchrotron Radiation (IPS), г. Карлсруэ, Германия) с использованием Сu-Кα излучения (λ=1,540 59 Å) от вращающегося анода. Нагрев производился в температурной камере Anton Paar DHS1100, контролируемой приставкой TCU200 Temperature Control Unit в температурном интервале от 300 до 500 K с шагом от 1 до 5 К в зависимости от силы рассеяния (структуры образца и толщины покрытия). Нагревательная база температурной камеры состоит из нитрида кремния. Для измерения интенсивности дифракционных максимумов был использован линейный счетчик D/teX Ultra с размером точки 0,10 мм от компании Rigaku. Ток и напряжение при измерении составили 45 кВ и 160-200 мА соответственно. Время одного измерения составило примерно 1,5 минуты.
Результаты исследования и их обсуждение
Экспериментальные результаты для исходного образца показали точное совпадение с теоретическим предсказанием в температурном интервале от 300 до 395 K. Дальнейшее нагревание вплоть до 480 К приводит к небольшим нелинейным отклонениям (рис. 3).

Рис. 3. Экспериментальные данные (черные точки) и теоретическое предсказание для линейной (красная линия) и полиномиальной (зеленая линия) теории поведения коэффициента теплового расширения для образца из золота, толщиной 30 мкм. Приведены данные для нагревания от комнатной температуры и последующего охлаждения до нее
Отклонение от теоретической прямой может свидетельствовать о нелинейности теплового расширения золота при нагреве до высоких температур. Кроме того, некоторые изменения структуры образца, частичный отжиг или механический гистерезис могут возникать при нагреве. Для аппроксимации экспериментальной зависимости может быть использована полиномиальная функция.
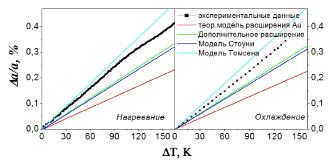
Рис. 4. Экспериментальные и теоретические кривые для образца 30AuCr при нагреве и охлаждении соответственно. На рисунке изображены теоретические линейные зависимости, описанные в методике
Нанесенная посредством термического напыления тонкая пленка образца 30AuCr демонстрирует широкую область линейности (рис. 4). Наклон кривой слегка изменяется только после 400 K, что может свидетельствовать о начале процесса отжига.
Наиболее близкой к экспериментальной кривой для 30AuCr является модель Томсена, однако она все же недостаточно хорошо аппроксимирует данные. Это может быть следствием пренебрежения вкладом расширения в плоскости образца, потому что сама подложка немного расширяется. К тому же пленка не полностью однородна и кристаллическая решетка может расширяться параллельно подложке для заполнения пробелов между кристаллитами. Это расширение спровоцирует частичную релаксацию напряжений и сдвинет кривую в область более низких значений.
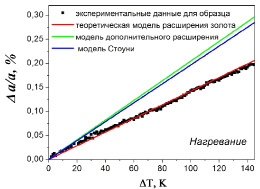
Рис. 5. Экспериментальная и теоретическая кривые для образца bbi100layer с покрытием из наночастиц; черные точки – экспериментальные данные, красная линия – расширение объемного образца
Термические свойства образцов из наночастиц в точности соответствуют поведению объемного образца. Это связано с тем, что наночастицы не ограничены подложкой и имеют пространство для расширения вокруг них. Эта теория хорошо согласуется с экспериментальными результатами (рис. 5).
Выводы
Тепловое расширение золотой пластины коррелирует с теоретическим предсказанием с небольшим отклонением, связанным нелинейной зависимостью с КТР, начинавшейся с 400 К и усиливающейся при дальнейшем нагревании. Термические свойства образцов из наночастиц в точности соответствуют поведению объемного образца.
Для нанесенной термическим напылением пленки толщиной 30 нм нагревание до 430 К не приводит к значительным изменениям, расширение происходит линейно в температурном диапазоне от 300 до 430 К, наблюдаются незначительные отклонения, косвенно свидетельствующие о начале процесса отжига. Наклон кривой в линейном диапазоне почти одинаков и ближе всего к кривой Томсена, но все еще немного ниже. Это может быть следствием расширения кристаллической решетки в плоскости пленки за счет ее несовершенств и пустот между зернами.
Библиографическая ссылка
Захарова М.А., Кудрявцева В.Л., Чудинова Е.А., Ерофеева Г.В. ТЕПЛОВОЕ РАСШИРЕНИЕ ТОНКИХ ПЛЕНОК РАЗЛИЧНОЙ СТРУКТУРЫ ПРИ НАГРЕВАНИИ // Современные наукоемкие технологии. 2015. № 2. С. 58-63;URL: https://top-technologies.ru/ru/article/view?id=34885 (дата обращения: 24.01.2026).



