Существуют различные подходы к моделированию процессов, протекающих в сложных технологических системах. Одним из наиболее распространенных методов является моделирование на основе систем дифференциальных уравнений, описывающих как отдельные подсистемы, так и объект в целом [3]. Однако для разработки таких моделей нужно сформулировать систему уравнений хотя бы на феноменологическом уровне, что не всегда представляется возможным.
В частности, в различных типах аккумуляторов наблюдается крайне неприятное явление теплового разгона. В настоящее время теория этого явления не разработана, в связи с чем практически отсутствуют попытки его математического моделирования.
В настоящей работе мы предлагаем для прогнозирования теплового разгона использовать алгоритм нечеткой логики, который позволяет проводить вычисления в условиях неполной и/или неточной информации. Также мы провели сравнение полученных результатов с имеющимися в литературе экспериментальными данными.
Поскольку наиболее удобным в данном случае является табличный способ ввода и визуализации вычислений, наиболее подходящим инструментом для вычислений мы считаем электронные таблицы Excel. Электронные таблицы Ехсеl отличаются уровнем функциональности, позволяющим рассматривать их как мощные системы математического моделирования и поддержки принятия решений. К наиболее существенным достоинствам электронных таблиц для научных исследований следует отнести широкие возможности математического, статистического и графического анализа данных, эффективное моделирование проблем типа «что будет, если», а также возможность разработки собственных приложений на языке программирования высокого уровня Visual Basic for Application (VВA). Методика разработки приложений нечеткой логики в Excel подробно изложена в [4].
Описание алгоритма
Все использованные нами функции принадлежности были трапециевидными. Пример кода для создания трапециевидной функции принадлежности, часто появляющейся в теории нечетких множеств, приведен в [4]. При вызове функции (категория «Определенные пользователем») появляется окно, показанное на рис. 1.
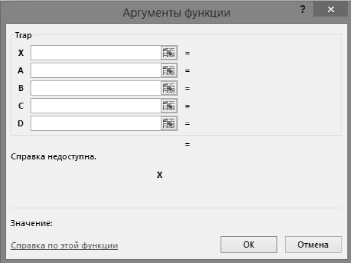
Рис. 1. Окно вызова для вычисления значений трапециевидной функции принадлежности
Пример графика трапециевидной функции принадлежности показан на рис. 2, где выделены точки, х-координаты которых соответствуют параметрам трапеции a, b, c, d. В данном случае a = 300, b = 500, c = d = 700.
Следуя подходу, изложенному в [2], исследование проводится по следующему алгоритму:
1) определяется система показателей и нечетких переменных, описывающих исследуемый процесс, и формируется соответствующее каждому показателю терм-множество значений;
2) для каждого показателя определяется уровень значимости; если все показатели считаются равнозначными, уровень значимости каждого показателя равен 1/N, где N – число показателей;
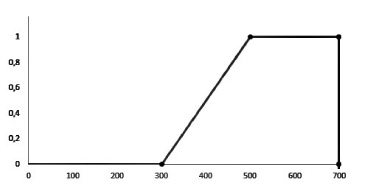
Рис. 2. Пример трапециевидной функции принадлежности
3) задаются текущие значения всех показателей и определяются соответствующие им значения функций принадлежности λij для i-го показателя и j-го нечеткого подмножества из общего количества нечетких подмножеств m, где m – число нечетких подмножеств выходной переменной;
4) строится классификация результирующего показателя g и вычисляется его значение по формуле:
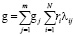 .
.
Здесь ri – уровень значимости i-го показателя; gj = 0.9 – 0.2(j – 1).
Оценка риска развития теплового разгона в аккумуляторах
В настоящее время во многих приборах бытового и специального назначения (мобильные телефоны, резервные источники питания и т.п.) устанавливаются различные типы аккумуляторов. Поэтому крайне важно знать факторы, которые могут нарушить стабильную работу аккумуляторов, а, следовательно, и всей системы. Одним из таких факторов может быть явление теплового разгона [1]. В результате теплового разгона происходит мощное выделение энергии, которое вызывает резкое повышение температуры внутри аккумулятора, что, в свою очередь, приводит к прогоранию сепаратора между пластинами и вскипанию электролита. Тепловой разгон неминуемо приводит к выходу системы из строя или сбоям в работе и, следовательно, является серьезным препятствием в работе очень большого числа современных приборов и систем.
Как отмечено в [1], тепловой разгон наблюдается в различных типах аккумуляторов: никель-кадмиевых, свинцово-кислотных, литиевых.
Причины теплового разгона в настоящее время неясны, в связи с чем практически отсутствуют попытки математического моделирования этого процесса, что не позволяет надежно предсказать его возникновение, или, по крайней мере, оценить предрасположенность различных аккумуляторов к тепловому разгону. Однако известно, что это явление происходит, как правило, в аккумуляторах с большим сроком эксплуатации в условиях длительного перезаряда.
Из экспериментальных данных [1] можно сделать следующие выводы:
Явление теплового разгона является случайным и достаточно редким.
Во всех случаях наблюдения теплового разгона в [1] заряд аккумуляторов выполнялся при напряжениях 2,2 В, что значительно превышает среднее напряжение эксплуатации данных аккумуляторов на объекте 1,35–1,5 В. Таким образом, можно утверждать, что вероятность теплового разгона повышается с ростом напряжения заряда аккумуляторов.
Для начала теплового разгона важна общая масса аккумуляторов и общий ток заряда. Вероятность теплового разгона уменьшается с уменьшением емкости аккумулятора.
Тепловой разгон никогда не возникает в новых аккумуляторах или в аккумуляторах с небольшим сроком эксплуатации. В данных [1] во всех случаях теплового разгона аккумуляторы имели сроки эксплуатации больше пяти лет при гарантийном сроке службы в три года. Можно считать, что вероятность появления теплового разгона увеличивается с ростом срока эксплуатации аккумуляторов.
Для прогнозирования явления теплового разгона мы ввели следующие нечеткие переменные: «Высокая температура», «Высокое напряжение», «Большая емкость», «Большой срок эксплуатации».
Для выходной переменной, характеризующей риск развития теплового разгона, нечеткая переменная имеет терм-множество {«Высокий»}. Для простоты мы пока не рассматривали другие значения, которые планируем ввести (например, «Средний» и «Низкий»). Соответственно, переменная m имеет значение, равное 1.
Исходя из сделанных выше выводов, можно определить трапециевидные функции принадлежности переменных следующим образом:
• функция принадлежности переменной «Высокая температура» с параметрами [200; 400; 700; 700];
• функция принадлежности переменной «Высокое напряжение» с параметрами [2; 2,5; 4; 4];
• функция принадлежности переменной «Большая емкость» с параметрами [24; 48; 60; 60];
• функция принадлежности переменной «Срок эксплуатации» с параметрами [5; 8; 15; 15].
Параметр g вычисляется аналогично предыдущему пункту и оценивает степень риска развития теплового разгона.
Пример вычислений показан на рис. 3. В нашем случае значения j = 2 и j = 3 не используются, поэтому соответствующие значения gj приняты равными нулю.
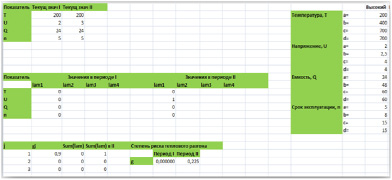
Рис. 3. Фрагмент вычислений риска теплового разгона в никель-кадмиевых аккумуляторах
Наши вычисления подтверждают экспериментальные выводы [1], что в некоторых партиях аккумуляторов тепловой разгон не наблюдается при очень большом числе циклов (несколько тысяч). В другой же партии тех же самых аккумуляторов с тем же сроком эксплуатации тепловой разгон происходит довольно легко, если применять жесткие режимы заряда (т.е. вести заряд при больших напряжениях заряда). Кроме того, как видно из рис. 3, на возникновение теплового разгона влияет достаточно большое повышение температуры и емкости аккумулятора.
Библиографическая ссылка
Семененко М.Г., Черняев С.И. РАЗРАБОТКА ПРИЛОЖЕНИЙ НЕЧЕТКОЙ ЛОГИКИ ДЛЯ ПРОГНОЗИРОВАНИЯ СЛУЧАЙНЫХ ЯВЛЕНИЙ В ТЕХНИЧЕСКИХ УСТРОЙСТВАХ // Современные наукоемкие технологии. 2014. № 12-1. С. 24-27;URL: https://top-technologies.ru/ru/article/view?id=34803 (дата обращения: 09.03.2026).



