Известно, что применение алгебраических структур, обладающих свойством кольца и поля, позволяет выполнить алгоритмы цифровой обработки сигналов (ЦОС) в реальном масштабе времени. Так как базовыми операциями ЦОС являются операции сложения, вычитания и умножения, то эти операции можно эффективно реализовать с использованием модулярной арифметики. Именно такие операции составляют основу алгоритмов крупномасштабного анализа сигналов. Поэтому реализация дискретного вейвлет-преобразований в поле является актуальной задачей.
Постановка и решение задачи исследований
Модулярная арифметика в настоящее время расширяет сферу своего использования. В настоящее время в качестве основных направлений применения алгебраических структур, обладающих свойством кольца и поля, можно выделить:
– Цифровая обработка сигналов. В данной области достаточно много трудов связано с использованием математических моделей ортогональных преобразований сигналов в поле комплексных чисел, которые реализуются на основе системы остаточных классов (СОК). Использование модулярных кодов позволяет, кроме повышения производительности специализированных процессоров (СП) ЦОС, обеспечить высокую отказоустойчивость вычислительных устройств [1, 2]. С целью повышения точности обработки сигналов в ряде работ [3–5] предлагается выполнение алгоритмов ЦОС в кольце полиномов. Использование полиномиальной системы классов вычетов способствует повышению снижения погрешности при проведении ортогональных преобразований сигналов. Кроме того, подобно кодам СОК, полиномиальная система классов вычетов позволяет осуществлять поиск и коррекцию ошибок, возникающих в процессе функционирования спецпроцессоров ЦОС.
– Защита информации от несанкционированного доступа (НСД) на основе криптографических алгоритмов. Использование математических особенностей полей Галуа позволяет отказаться от операции суммирования по модулю и использовать мультипликативные операции по модулю и их комбинации [6–8]. Использование модулярных полиномиальных кодов позволяет обеспечить защиту потока данных в реальном масштабе времени.
– Построение псевдослучайных функций (ПСФ) повышенной эффективности. В работе [9] представлен алгоритм и основные сферы применения разработанной ПСФ, реализованной в конечном поле. Данная псевдослучайная функция в качестве аргумента использует входную последовательность (х1,…,хn) и ключи (g,s1,…,sn). В результате алгоритм ее вычисления определяется
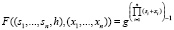, (1)
где h – первообразный элемент мультипликативной группы.
Проведенные исследования показали, что для области определения размером 2m значение n = m/log2l. Вследствие этого при вычислении данной функции требуется в log2l раз меньше умножений. Основным преимуществом данной ПСФ является использование меньшего объема памяти для вычисления значения функция, так как она использует ключ в log2l раз меньший размером по сравнения с ПСФ Наора-Рейнголда. При этом стойкость данной ПСФ основывается на предположении о сложности решения l-DDH проблемы.
Одним из наиболее перспективных направлением применения модулярной арифметики, реализованной в конечном поле, является крупномасштабный анализ сигналов. Известно, что дискретное преобразование Фурье (ДПФ), а также быстрое преобразование Фурье (БПФ) не используют для проведения анализа нестационарных сигналов, локализованных в некотором интервале времени. Это обусловлено тем, что ДПФ и БПФ не позволяют получить информацию о динамике изменения сигнала во временной области. Таким образом, ортогональные преобразования сигналов, проводимых в поле комплексных чисел, не позволяют правильно оценить изменения частотно-временных характеристик сигнала.
Данного недостатка лишены вейвлет-преобразования, которые положены в основу крупномасштабного анализа сигналов. Использование дискретного вейвлет-преобразования (ДВП) позволяет получить истинную картину при анализе сигнала, так как это преобразование производится как во временной области, так и в частотной области.
Одним из первых дискретных вейвлет-преобразований является преобразование Хаара, которое относится к разделимым, и может быть представлено в виде матриц
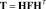, (2)
где F – матрица сигнала; H – матрица преобразования; T – результат преобразования сигнала.
Для построения матрицы преобразования Хаара используются базисные функции Хаара hk(z). Следует отметить, что данные функции задаются на непрерывном замкнутом интервале z∈[0, 1]. Используемые при этом значения переменной k, располагаются в пределе от 0 до N-1, где N = 2n. При этом для каждого индекса k, определяется пара значений q и l, для которых справедливо,
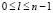, (3)
так чтобы выполнялось условие
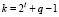. (4)
В работе [10] представлен алгоритм выбора значения индекса, согласно которому
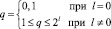(5)
Вычисленные, согласно выражения (5), значения индексов l и q используются для вычисления базисных функции Хаара. Если k = 0, то базисная функция имеет вид
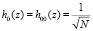, (6)
где z∈[0, 1].
При этом для вычисления остальных базисных функций используется выражение
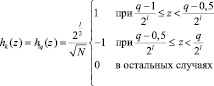, (7)
где z∈[0, 1].
Рассмотрим выполнение вейвлет преобразования Хаара для 8 точек. Тогда матрица преобразования Хаара будет иметь следующий вид
(8)
Анализ выражения (8) показывает, что преобразование Хаара можно реализовать в конечном поле GF(р), где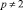 
. Это обусловлено тем, что матрица содержит целые числа. Однако в ней присутствует и корень из двух. Переход к вычислению вейвлет Хаара возможно, если конечное поле сможет обеспечить целочисленное вычисление 
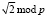. Данное свойство позволит осуществить переход от позиционного вычисления вейвлет-преобразования Хаара к преобразованию Хаара в конечном поле.
Выберем конечное поле GF(17), в котором существует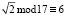 
. При этом значение нормирующего множителя в данном поле будет равно 
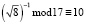. В этом случае получаем следующую матрицу вейвлет-преобразования Хаара
(9)
Для удобства работы в конечном поле произведем нормализацию 8×8 матрицы преобразования Н8 в поле GF(17)
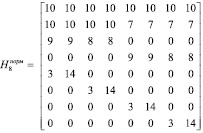(10)
В данной матрице выполняются все требования, предъявляемые к вейвлет-преобразованию
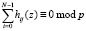. (11)
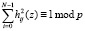. (12)
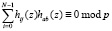, (13)
где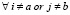 
.
Произведем выполнение крупномасштабного анализа сигнала с использованием нормализованной матрицы Хаара в конечном поле GF(17).
. (14)
Проведем прямое преобразование Хаара для входной последовательности отсчетов сигнала f(x) = [1, 1, 4, 4, 0, 0, 0, 1]. Тогда, используя математический аппарат, который связан с крупномасштабной теорией, имеем
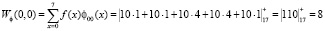
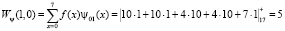
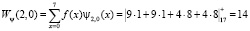
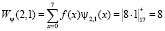
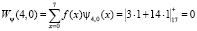
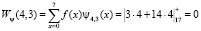
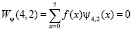
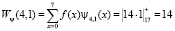
Таким образом, результатом вейвлет-преобразования имеем
.
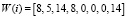Произведем обратное преобразование с целью восстановления исходного сигнала. Для этого необходимо воспользоваться транспонированной матрицей Хаара 
, которая в конечном поле GF(17) имеет следующий вид
. (15)
Воспользуемся данной матрицей и произведем вычисление обратного преобразования. В качестве входного вектора используем
.
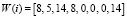Тогда имеем
. (16)
Согласно (16) получаем
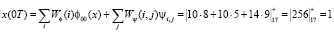
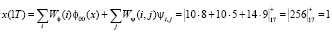
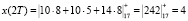
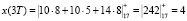
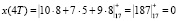
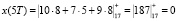
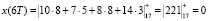
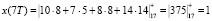
Таким образом, получена исходная входная комбинация, которую подвергали крупномасштабному анализу. Рассмотрим представление исходной последовательности в базисе вейвлет-преобразования
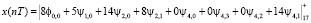, (17)
Таким образом, выражение (17) можно представить в виде
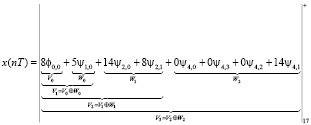. (18)
Проведенные исследования свидетельствуют о том, что использование вейвлет-преобразований в конечном поле представляет собой обратимые преобразования. При этом такое преобразование не имеет ошибок округления, которые определяются позиционной системой счисления.
Выводы
В работе рассмотрены вопросы применения вейвлет-преобразований для анализа сигнала. В качестве такого преобразования предлагается использовать преобразования Хаара. Показана целесообразность реализации данного преобразования в конечном поле. Приведены примеры прямого преобразования Хаара, а также реализация обратного преобразования в поле Галуа GF(17). Полученные результаты позволяют сделать вывод о том, что использование алгебраических структур, обладающих свойством поля, позволяет снизить ошибки округления при выполнении крупномасштабного анализа сигналов.
Библиографическая ссылка
Калмыков И.А., Ложечкин А.А., Гапочкин А.В., Калмыков М.И. АЛГОРИТМ ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ ХААРА В КОНЕЧНОМ ПОЛЕ // Современные наукоемкие технологии. – 2014. – № 11. – С. 18-23;URL: https://top-technologies.ru/ru/article/view?id=34765 (дата обращения: 21.11.2024).