Как известно, Ф. Клейн в своей работе [1] уточняет: «…разделяют два рода геометрий: геометрия синтетическая…и…геометрия аналитическая... Кроме этих двух…можно еще рассматривать третий род,…являющийся обобщением двух первых».
В настоящей статье для исследований попытаемся использовать третий род геометрий.
Известно, что одна из синтетических геометрий называется начертательной геометрий, которая изучает методы отображения пространственных форм на плоскость.
При этом в процессе отображения участвуют:
– оригинал,
– аппарат отображения,
– модель (изображение),
– носитель модели.
В качестве оригинала могут выступать любые объекты пространства, простейшим из которых является точка, однозначно определяемая тремя координатами, с мерностью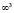 
(точка на поверхности (плоскости) имеет мерность 
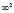, точка на кривой (прямой) имеет мерность 
).
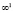В качестве аппарата отображения используются кривые (прямые) или поверхности (плоскости).
Тогда моделью (изображением) точки будет точка – при проецировании кривой (прямой) или кривой (прямой) при проецировании поверхностью (плоскостью).
Ясно, что носителем модели может быть поверхность (плоскость) или кривая (прямая).
Мы для изложения из всего выше сказанного возьмем в качестве оригинала точку, тогда у нас будут:
- оригинал – точка,
- аппарат отображения – связка
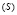или связки прямых, - модель – точка или точки,
- носитель модели – плоскость.
При этом необходимым требованием для проецирования точек пространства, имеющей мерность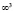 
, является условие, чтобы модель ее имела мерность 
.
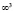Аппаратом проецирования являются связки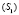 
и 
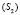прямых, а носитель модели плоскость 
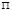. Точку C пространства спроецируем из центра 
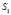в точку 
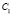на плоскость П (рис. 1), имеющей мерность 
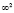при чем в точку С1 проецируются все точки луча 
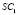. Чтобы выполнить требование проецирования, возьмем еще один центр проецирования 
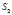, при этом точк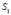и 
и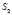 
определят в пространстве прямую m, которая пересечет плоскость 
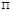в точке 
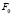, постоянную для данного аппарата проецирования, выделяющая на плоскости 
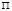пучок (
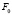) прямых. Точка 
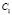из пучка (
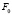) прямых выделит прямую c, на которую спроецируем точку C из центра 
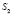в точку 
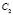с мерностью 
.
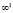В результате имеем на плоскости П модель точки C – пару точек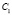 
и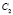 
.
Тогда мерность модели будет равна
.
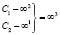Откуда видно, что мерности оригинала и модели равны.
Если в качестве оригинала будет выступать тело, то оно пучком (m) плоскостей будет расслаиваться на сечения, которые из центров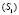 
и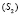 
проецирования будут моделироваться в пучке 
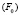прямых на плоскости П.
Отметим, что в оригинале точки могут быть: простая (точка C), двойная (точка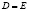 
), конкурирующие (точки A и B) (рис. 1). Ясно, что проекции точек A и B из центра проецирования 
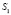на носитель модели прямую 
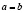проецируются в конкурирующие точки 
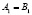, а из центра 
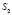проецируются в пару точек 
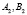. Тогда двойная точка 
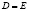моделируется из центров проецирования 
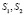на носителе модели 
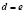двойными точкам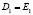и 
и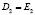 
.
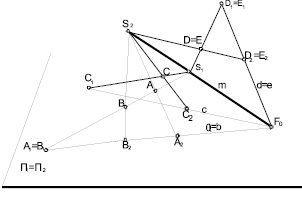
Рис. 1
Как известно [1, 2], на плоскости определяются точки, прямые, кривые второго порядка, плоские кривые третьего, четвертого и т.д. порядков.
При этом точка – это элемент плоскости и пространства никак не определенный, а взятый как данность, не имеющая мерности, т.е. нульмерная величина.
Прямая, имеющая протяженность – одномерная величина, она на плоскости определяется двумя точками.
Кривая второго порядка определяется на плоскости 5 точками.
Плоская кривая третьего порядка определяется 9 точками.
Плоская кривая четвертого порядка, определяется 14 точками и кривая n-го порядка, определяется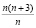 
точками.
Так как две прямые на аффинной плоскости могут пересекаться или не пересекаться, если они параллельны. Значит между точками и прямыми на аффинной плоскости не существует взаимно однозначного соответствия.
Для устранения этой неопределенности условились [1, 2, 3 и др.], что параллельные прямые пересекаются в несобственной точке, находящейся на несобственной прямой, введенной на аффинной плоскости и превратившей аффинную плоскость в проективную. Так как на проективной плоскости любые прямые пересекаются, то этим устанавливается взаимно однозначное соответствие между точками и прямыми плоскости. Как отмечалось выше, прямая на аффинной плоскости определяется двумя точками, и если ее рассматривать как числовую ось, взяв на ней точку O – начало отсчета и единицу отчета – точку 1, то двигаясь от точки O вправо мы будем двигаться к точке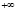 
, а двигаясь от точки O влево – к точке 
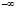, числовой оси, где число 
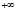самое большое, а число 
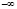– самое маленькое. На проективной плоскости, рассматривая прямую как замкнутую линию точкой 
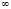, в которую проецируются две конкурирующие точк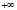и 
и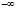 
, то точка 
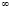является третья несобственная точка на этой прямой. Поэтому проективную прямую можно рассматривать как окружность бесконечного радиуса, представляющую распавшуюся окружность на две пересекающиеся прямые – несобственную прямую и на проективную прямую.
В работе автором [4] доказано, что проекции точек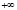 
и 
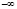на проективной плоскости совпадают, являясь конкурирующими точками. Действительно, так как оригинал проективной прямой представляет виток винтовой линии a, где точки 
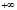и 
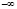конкурирующие, лежащие на одном проецирующем луче, то проективная прямая плоскости 
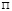есть замкнутая линия 
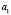с простыми точками, как, например, 
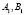и т.д., и совпавшими проекциями конкурирующих точек 
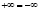(рис. 2).
Таким образом, введение несобственных точек в проективной геометрии на прямой позволило упростить многие предложения, например, две прямые на плоскости теперь всегда пересекаются. Поэтому можно утверждать, что при движении в любом направлении по прямой мы можем через бесконечную точку вернуться в исходную точку. Такую прямую назвали проективной прямой, а плоскость – проективной плоскостью, а пространство – проективным пространством. Используя доказанную автором теорему из [4] можно сказать, что все несобственные точки прямых проективной плоскости образуют двойную несобственную прямую плоскости. То есть несобственная прямая проективной плоскости двойная по образованию. По принципу двойственности несобственной прямой проективной плоскости многие понятия и определения становятся очевидными. Таким образом, известно, что прямая на аффинной плоскости двусторонняя и сама аффинная плоскость двусторонняя. Проективная прямая на проективной плоскости отличается от прямой аффинной плоскости наличием на ней совпавших проекций конкурирующих точек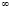 
и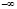 
. То есть она является двусторонней. Так как на проективной плоскости происходит замыкание, подобно застежки «молнии», по точкам 
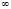и 
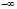несобственной прямой, поэтому проективная плоскость односторонняя. Другими словами, оригинал проективной плоскости, представляет виток винтовой поверхности, которая двусторонняя.
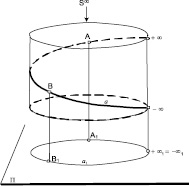
Рис. 2
В этом свете рассмотрим, как себя ведут кривые второго порядка относительно несобственной прямой.
1) Эллипс, уравнение которого на плоскости в прямоугольной системе координат имеет вид
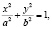(1)
где а – большая полуось, b – малая полуось эллипса, т.е.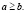 
Запишем уравнение эллипса в однородных координатах
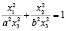
или
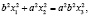
где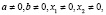 
то 
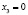имеем
,
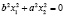которое разлагается на два уравнения прямых
,
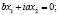
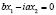представляющие собой две мнимо сопряженные прямые, пересекающие несобственную прямую в точках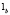 
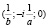и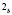 
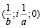. То есть, точк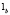и 
и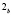 
меняют свое положение на несобственной прямой в зависимости от изменения параметров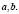 
2. Аналогично рассуждая для любой окружности, получим две фиксированные точки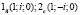 
, пересечения с несобственной прямой 
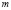, которые называются круговыми точками, прямые, проходящие через круговые точки, называются изотропными прямыми.
3. Гиперболы пересекают несобственную прямую в двух переменных действительных точках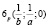 
, 
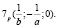Равнобочные гиперболы пересекают несобственную прямую в двух действительных неподвижных точках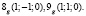 
4. Парабола имеет с несобственной прямой одну действительную неподвижную точку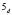 
(рис. 3).
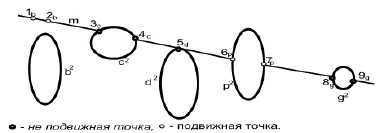
Рис. 3
Известно, что эксцентриситеты кривых второго порядка следующие: эллипса равен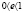 
; окружности равен 
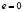; параболы равен 
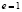; гиперболы равен 
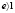; равнобочной гиперболы равен 
.
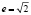На числовой оси е они расположатся так, как на рис. 4.
Рис. 4
Таким образом, можно высказать предложение:
Фиксированные значения эксцентриситетов кривых второго порядка соответствуют неподвижным точкам пересечения кривых второго порядка с несобственной прямой.
Выводы
1. Модель проективной прямой представляет собой замкнутую линию. Замыкание происходит по конкурирующим точкам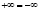 
.
2. Оригинал проективной прямой представляет разомкнутую линию в виде витка винтовой линии (см. рис. 2).
3. Модель проективной плоскости представляет собой одностороннюю поверхность. Замыкание происходит по несобственной прямой.
4. Оригинал проективной плоскости представляет собой виток винтовой двусторонней поверхности.
5. Несобственная прямая является двойной.
6. Любая точка проективной плоскости определяет пучок прямых, в каждый из которых входят две изотропные прямые, оси эллипсов, асимптоты гипербол, ось парабол.
7. Точки несобственной прямой определяют пучки параллельных прямых.
8. Кривые второго порядка ведут себя на проективной плоскости относительно несобственной прямой особенно: окружность, парабола и равнобочная гипербола пересекают ее в фиксированных точках, эллипсы и гиперболы пересекают ее в переменных точках в зависимости от значений их параметров.
9. Значения эксцентриситетов кривых второго порядка определяются типом точек пересечения кривых второго порядка с несобственной прямой.
Библиографическая ссылка
Вертинская Н.Д. О НЕКОТОРЫХ ОСОБЕННОСТЯХ ПОВЕДЕНИЯ КРИВЫХ ВТОРОГО ПОРЯДКА НА ПРОЕКТИВНОЙ ПЛОСКОСТИ // Современные наукоемкие технологии. – 2014. – № 10. – С. 124-127;URL: https://top-technologies.ru/ru/article/view?id=34760 (дата обращения: 21.11.2024).