Электромагнитные механоактиваторы (ЭММА) унифицированной формы исполнения [1, 2, 3], у которых рабочий объем выполнен в форме кольца, конуса или многоугольной формы в поперечном сечении рабочей камеры, предназначены для переработки дисперсной фазы в дисперсионной среде при одновременном перемешивании и гомогенизации технологических сред [4, 5, 6, 7]. Они реализуют способ обработки материалов в тонком слое и позволяют осуществлять как раздельные, так и совмещенные стадии тонкого и сверхтонкого диспергирования и механоактивации частиц с различными свойствами: твердых скалывающихся, хрупких, средней твердости, упругих мягких Условием получения продукта с ровным гранулометрическим составом в узком диапазоне дисперсности при обработке в ЭММА унифицированной формы является равномерное распределение силовых нагрузок в рабочем объеме [8,9]. Силы воздействия между размольными ферромагнитными элементами в определены по формуле [10, 11, 12]:
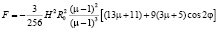
(здесь μ – магнитная проницаемость размольных элементов; Н – напряжённость электромагнитного поля, принимающая значение Н1 во внешней части камеры механоактиватора, либо значение Н2 – во внутренней части механоактиватора; R0 – радиус размольных элементов; φ – угол деформации структурной цепочки). Выявлено, что сила взаимодействия принимает максимальное значение при φ = 0:
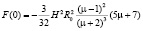 .
.
При этом структурные построения из ферроэлементов параллельны линиям вектора напряжения электромагнитного поля. При смещении поверхностей рабочего объема относительно друг друга происходит изменение угла деформации φ. Структурные построения из ферроэлементов деформируются, угол φ увеличивается, а сила притяжения уменьшается. При некотором критическом значении угла деформации
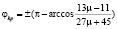
сила притяжения ферроэлементов станет равной нулю F(φкр) = 0, а при дальнейшем увеличении угла обратится в силу отталкивания. При определении сил следует учитывать, что взаимодействие ферроэлементов в магнитоожиженном слое происходит через прослойку обрабатываемого продукта. Если исходный размер частиц продукта принять равным rn, то формула для определения силы взаимодействия примет вид:
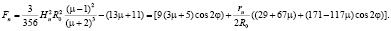
Величина критического угла определена по формуле:
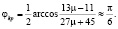
В процессе деформации структурной группы угол φ увеличивается. При этом на контактную систему из двух ферроэлементов начинает действовать момент, стремящийся вернуть цепочку в первоначальное (совпадающее с направлением силовых линий) положение. Приняв во внимание наличие продукта между размольными элементами, величину момента можно определить по формуле
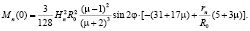
Из анализа формулы следует, что при φ = 0 и при φ = π/2 момент обращается в ноль. В случае, когда φ = 0 сила взаимодействия ферроэлементов максимальна, а находящийся между ними продукт испытывает наибольшее раздавливающее усилие. По мере того, как поверхности смещаются друг относительно друга, величина угла растет, увеличивается вращательный момент, действующий на структурные построения из ферроэлементов. При достижении угла деформации критического значения φ = φкр цепочки разрушаются и вся потенциальная энергия переходит в кинетическую. Ферроэлементы из разрушенной цепочки образуют новое структурное построение, направление которого совпадает с направлением силовых линий электромагнитного поля и зависит от конструктивного исполнения аппарата. При этом продукт, находящийся в смеси с размольными элементами, испытывает энергонапряженное силовое воздействие и измельчается ударно-истирающими нагрузками [4, 5]. Достоверность результатов теоретических исследований подтверждена экспериментом с применением программных комплексов ANSYS [13, 14, 15].
Библиографическая ссылка
Беззубцева М.М., Ружьев В.А., Загаевски Н.Н. ФОРМИРОВАНИЕ ДИСПЕРГИРУЮЩИХ НАГРУЗОК В МАГНИТООЖИЖЕННОМ СЛОЕ ЭЛЕКТРОМАГНИТНЫХ МЕХАНОАКТИВАТОРОВ // Современные наукоемкие технологии. 2014. № 10. С. 78-80;URL: https://top-technologies.ru/ru/article/view?id=34736 (дата обращения: 29.01.2026).



