Со времени И. Ньютона гравитационное поле планеты обычно представляют в виде шаровых функций, т.е. планету разбивают на шаровые поверхности. Массу каждой шаровой поверхности после интегрирования рассматривают сосредоточенной в ее центре. Интегрирование по объему планеты сводится к интегрированию шаровых поверхностей и приводит к сосредоточению массы планеты в ее центре, т.е. к традиционным представлениям о гравитационном поле планеты.
Целью работы является, в отличие от традиционного, показать иной путь интегрирования для получения уравнения напряженности гравитационного поля в точке на удалении от однородного шарообразного тела. Это тело мы разбиваем на элементы в виде дисков и проводим интегрирование по указанным элементам шарообразного тела (см. рисунок).
Решаемая задача: Показать, что результат интегрирования шарового тела по вкладу дисков в величину ускорения силы тяжести в точке А (g) на удалении (h) от однородного сферического тела соответствует закону всемирного тяготения.
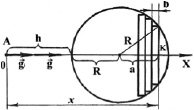
Обозначения: x – расстояние от точки А до диска; R – радиус сферического тела; а – расстояние от центра сферического тела до диска; К – радиус диска; b – ширина диска
Выполнение интегрирования. Для интегрирования используем формулу (9) нашей статьи [1]. Подкоренное выражение этой формулы преобразуем:
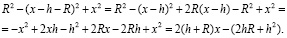 (1)
(1)
Найдем сначала способом подстановки неопределенный интеграл:
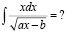 (2)
(2)
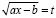 ;
; 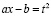 ;
; 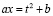 ;
;
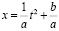 ;
;
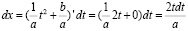 .
.
Подставим в (2), получим:
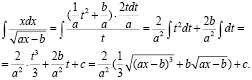 (3)
(3)
Интеграл по уравнению (1) можно будет взять, используя уравнение (3):
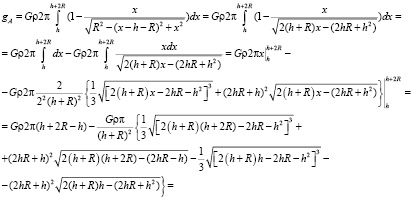
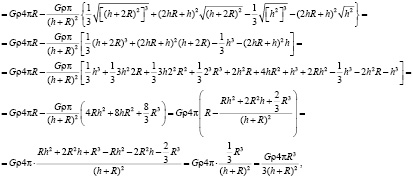
Или
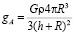 . (4)
. (4)
Т.е. результат интегрирования шарового тела по вкладу дисков в величину ускорения силы тяжести соответствует закону всемирного тяготения. В своих исследованиях мы, подобно представлению классической теории тяготения и общей теории относительности, исходили из идеальной проницаемости вещества гравитационным полем, т.е. из отсутствия поглощения гравитационного поля веществом. Мы считали, что поле от последующих дисков без ослабления пронизывает предыдущие диски. Поиски гравитационной экранировки давали до сих пор отрицательный результат. Однако сообщения об аномальных гравитационных эффектах периодически появляются. Так, китайские ученые (Ванг и его коллеги) зафиксировали ослабление притяжения Земли к Солнцу во время Солнечного затмения в марте 1997 года [2]. Вывод китайских ученых нуждается в тщательной проверке.
Найдем положение диска, дающего максимальный вклад в ускорение силы тяжести (gi max ) по рис. 5 статьи [1] путем классического поиска экстремума. В исследуемом уравнении
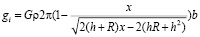
gi будет максимальным, если
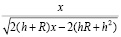
будет минимальным. Возьмем производную этого выражения:
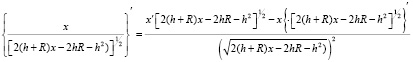 .
.
Числитель приравниваем нулю, получим:
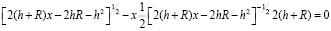 .
.
Откуда:
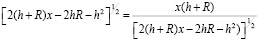 ,
,
или
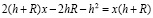 ,
,
откуда
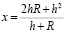 ,
,
или
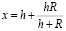 ;
;
т.е. 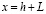 ,
,
где
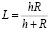 , (5)
, (5)
что соответствует уравнению (13), полученному эвристическим методом, нашей статьи [1]. В уравнении (5) L – глубина расположение диска (дающего максимальный вклад в ускорение силы тяжести в точке А) от поверхности сферического тела. Уравнение (5) можно преобразовать в уравнение
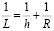 , (6)
, (6)
которое удобно для анализа граничных условий. Так, при h=0 также L→0. И это давно известно для Земли в общей физике и геодезии; а при h→∞, или h>> R, L=R, т.е. диск, определяющий gi max, проходит через центр сферического тела, и имеет самый большой диаметр, поэтому дает максимальный вклад, что также является очевидным. Проведенный выше анализ показывает работоспособность полученных уравнений (5) или (6).
Интерпретация полученных результатов. Вывод. Результат интегрирования шарового тела по вкладу дисков в величину ускорения силы тяжести (уравнение (4)) соответствует закону всемирного тяготения, т.е. найден иной путь интегрирования для получения уравнения напряженности гравитационного поля в точке на удалении от однородного шарообразного тела. Благодаря использованному подходу, обнаружено положение диска (уравнение (5)), дающего максимальный вклад в напряженность гравитационного поля в точке А на удалении от шарообразного тела – модели планеты. Обнаруженный эффект в его аналитическом виде является новым и позволяет раскрыть область его возможного использования.
Область возможного использования результатов. В геодезии различают два типа задач. Один тип – определение гравитационных характеристик поля планеты по структуре элементов Земли; другой тип – получение данных о структурных элементах Земли, например, поиск полезных ископаемых по данным гравитации. И это в большей мере используется для изучения лишь поверхностных структур Земли. Ранее такое изучение проводилось научными экспедициями, в том числе океанографическими (например, при поиске нефти). Затем стали использовать ИСЗ. Полученные нами результаты помогут в проведении подобных исследований, и, в особенности, глубинных структур Земли с помощью ИСЗ «при выборе отсчетов сигнала в зависимости от потенциальной значимости, заложенной в нем информации» [3].
Библиографическая ссылка
Борисов Ю.А., Габдрахманов К.Н. УЧЕБНЫЕ ИССЛЕДОВАНИЯ ГРАВИТАЦИИ (Ч. III) // Современные наукоемкие технологии. 2014. № 10. С. 42-45;URL: https://top-technologies.ru/ru/article/view?id=34721 (дата обращения: 09.03.2026).



