Структура современных спецпроцессоров (СП) цифровой обработки сигналов (ЦОС) очень насыщена и сложна. Применение параллельных алгоритмов ортогональных преобразований сигналов определяется требованием реального масштаба проводимых вычислений. При этом такие вычислительные устройства должны обладать свойством устойчивости к отказам, возникающим в процессе функционирования. Применение корректирующих кодов полиномиальной системы классов вычетов (ПСКВ) позволяет осуществлять поиск и коррекцию ошибок в реальном масштабе времени.
Основная часть. В современных условиях сохранение работоспособного состояния параллельных спецпроцессоров ЦОС во многом определяется быстротой и точностью определения местоположения и глубины ошибки, которая возникает из-за отказа оборудования. При этом предпочтение отдается информационной, а не технологической надежности системы, которая может быть достигнута путем специального кодирования, обеспечивающего обнаружение ошибок, возникающих в результате сбоев и отказов элементов системы, и их исправление [2-7].
В основу большинства алгоритмов и методов поиска и коррекции ошибок в модулярных кодах положена процедура вычисления позиционной характеристики. По способу построения процедур поиска и локализации ошибки в модулярных кодах существующие методы можно разделить на две основные группы. К первой относятся методы и алгоритмы контроля и коррекции ошибок кода ПСКВ, базирующиеся на вычисление позиционных характеристик во временной области [2-7, 9, 10]. Что касается процедур второй группы, то они реализуются в частотной области [1, 8]. Рассмотрим методы обнаружения и коррекции ошибок, работающие во временной области, а так же их реализацию в базисе нейросетевой логики.
Реализация данного подхода предполагает использование некоторого функционального отношения, однозначно отражающего множество значений модульных характеристик во множество рассматриваемых ошибок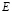 
. При этом необходимо, чтобы математическая модель, отражающая данное отношение, при реализации обеспечивала бы параллельно-конвейерную организацию вычислений.
В работе [4] доказана теорема о возможности использования непозиционных полиномиальных кодов в процедурах обнаружения и коррекции ошибок. С этой целью в модулярную комбинацию вводится дополнительное контрольное основание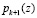 
, где k – количество рабочих оснований. При этом степень избыточного основания не должна быть меньше наибольшей степени рабочего основания. 
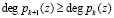. Однако проводимые исследования показали, что наличие одного избыточного основания, даже удовлетворяющего предельной теореме, является недостаточным, так как корректирующие способности такого кода не позволяют исправить однократные ошибки по всем основаниям ПСКВ [2].
Для решения данной проблемы необходимо осуществить логическое упрочнение контрольного основания. С этой целью вводится дополнительное контрольное основание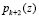 
, удовлетворяющее условию 
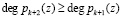. Однако упрочение контрольного основания требует значительного расширения диапазона обрабатываемых данных. В этом случае рабочий диапазон полиномиальной системы классов вычетов будет определяться
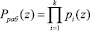, (1)
а полный диапазон системы задается выражением
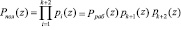. (2)
А чтобы точность представления не претерпела заметного уменьшения, надо увеличивать диапазон представления величин, и тогда их истинные (без введенной погрешности) значения будут в пределах заданного рабочего диапазона.
Альтернативным путем решения данной проблемы является метод определения правильности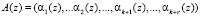 
на основе нулевизации, заключающейся в переходе от исходного полинома к полиному
,
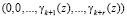при помощи преобразований, при которых не имеет место ни один выход за пределы рабочего диапазона системы.
Алгоритм процедуры нулевизации заключается в последовательном вычитании из исходного полинома, представленного в модулярном коде, некоторых минимальных полиномов – констант нулевизации таких, что полином А(z) последовательно преобразуется в полином вида
,
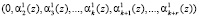затем в полином
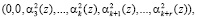
и так далее. Продолжая данный процесс в течение k итераций, получается
.
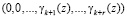Применение метода нулевизации позволяет последовательно получать наименьший полином, кратный сначала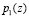 
, затем полином – кратный произведению 
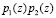, и в конечном итоге – кратный рабочему
.
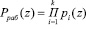Основным недостатком метода нулевизации [6, 9] является последовательный характер вычислительного процесса, что не позволяет реализовать его на основе двухслойной нейронной сети. Это обусловлено, прежде всего тем, что константы нулевизации представляют собой наименьшие возможные числа
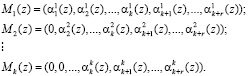(3)
где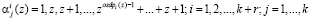 
.
Решить данную проблему можно за счет отказа от констант нулевизации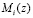 
и перехода к использованию псевдоортогональных полиномов. Если положить условие, ч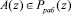то 
, то
.
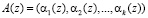Тогда, согласно китайской теореме об остатках, полином A(z) можно представить
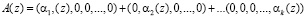. (4)
Каждое слагаемое выражения (4) представляет собой
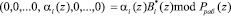, (5)
где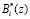 
– ортогональный базис, безизбыточной системы оснований.
Проведя расширение системы оснований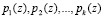 
на r контрольных 
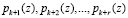, представим
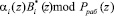
в виде
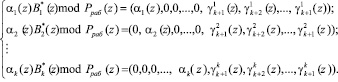(6)
Подставим выражения (6) в равенство (4).
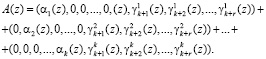(7)
Следовательно,
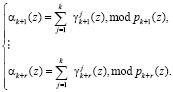(8)
Значит, разность полинома A(z), представленного в ПСКВ, и псевдоортогональных форм, полученных согласно (6), задаёт величину нормированного следа полинома
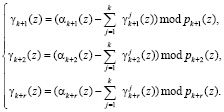(9)
Определим все псевдоортогональные полиномы для ПСКВ, в которой используются рабочие основания р1(z) =z+1, р2 (z)=z2+z+1, р3(z)=z4+z3+z2+z+1. В качестве контрольных оснований выбраны р4(z)=z4+z3+1 и р5(z)=z4+z+1. При вычислении псевдоортогональных базисов необходимо учитывать невозможность выхода за пределы рабочего диапазона Pраб(z) = z7 + z6 + z5 +...+ z2 +z +1. Полученные значения представлены в табл. 1.
Таблица 1
Псевдоортогональные полиномы ПСКВ поля GF(24)
|
Основание ПСКВ |
Псевдоортогональный полином |
|
р1(z) =z+1 |
(1, 0, 0, z3+z+1, z) |
|
р2 (z)=z2+z+1 |
(0, 1, 0, z2+z+1, z3+1) |
|
|
(0, z, 0, z3+z, z2+z+1) |
|
|
(0, z+1, 0, z3+z2+1, z3+z2+z) |
|
р3(z)=z4+z3+z2+z+1 |
(0, 0, 1, z3+z2+1, z3+z) |
|
|
(0, 0, z, z+1, z2+z+1) |
|
|
(0, 0, z+1, z3+z2+z, z3+z2+1) |
|
|
(0, 0, z2, z, z3) |
|
|
(0, 0, z2+1, z3+z2+z+1, z) |
|
|
(0, 0, z2+z, 1, z3+z2+z+1) |
|
|
(0, 0, z2+z+1, z3+z2, z2+1) |
|
|
(0, 0, z3, z2, z+1) |
|
|
(0, 0, z3+1, z3+1, z3+1) |
|
|
(0, 0, z3+z, z2+z+1, z2) |
|
|
(0, 0, z3+z+1, z3+z, z3+z2+z) |
|
|
(0, 0, z3+z2, z2+z, z3+z+1) |
|
|
(0, 0, z3+z2+1, z3+z+1, 1) |
|
|
(0, 0, z3+z2+z, z2+1, z3+z2) |
|
|
(0, 0, z3+z2+z+1, z3, z2+z) |
Так как константы нулевизации подобраны таким образом, что в процессе вычитания из исходного полинома A(z) псевдоортогональных форм (5) выход за пределы рабочего диапазона не осуществляется, то по результату (9) можно судить о правильности полинома A(z). Если система равенств (9) обращается в ноль, то исходный полином не содержит ошибки, в противном случае – A(z) является ошибочным. В табл. 2 представлены значения вектора ошибки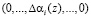 
для различных значений ошибки ПСКВ.
Таблица 2
Значения вектора ошибки модулярного кода поля GF(24)
|
Основание ПСКВ |
Значение вектора ошибки |
|
|
γ4(z) |
γ5(z) |
|
|
0 |
0 |
(0, 0, 0) |
|
z3+z+1 |
z |
(1, 0, 0) |
|
z2+z+1 |
z3+1 |
(0, 1, 0) |
|
z3+z |
z2+z+1 |
(0, z, 0) |
|
z3+z2+1 |
z3+z2+z |
(0, z+1, 0) |
|
z3+z2+1 |
z3+z |
(0, 0, 1) |
|
z+1 |
z2+z+1 |
(0, 0, z,) |
|
z3+z2+z |
z3+z2+1 |
(0, 0, z+1) |
|
z |
z3 |
(0, 0, z2) |
|
z3+z2+z+1 |
z |
(0, 0, z2+1) |
|
1 |
z3+z2+z+1 |
(0, 0, z2+z) |
|
z3+z2 |
z2+1 |
(0, 0, z2+z+1) |
|
z2 |
z+1 |
(0, 0, z3) |
|
z3+1 |
z3+1 |
(0, 0, z3+1) |
|
z2+z+1 |
z2 |
(0, 0, z3+z) |
|
z3+z |
z3+z2+z |
(0, 0, z3+z+1) |
|
z2+z |
z3+z+1 |
(0, 0, z3+z2) |
|
z3+z+1 |
1 |
(0, 0, z3+z2+1) |
|
z2+1 |
z3+z2 |
(0, 0, z3+z2+z) |
|
z3 |
z2+z |
(0, 0, z3+z2+z+1) |
Применение в качестве констант нулевизации псевдоортогональных полиномов позволяет перейти от последовательной реализации метода нулевизации к параллельной. В связи с этим открываются дополнительные возможности по сокращению временных затрат на реализации процесса определения местоположения ошибки и ее глубины.
Для эффективной реализации математических моделей вычислительных устройств, определенных над конечными полями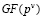 
или кольцами, необходимо, чтобы арифметические устройства могли эффективно реализовать основные операции данных алгебраических систем. В работе [9] приведена разработанная структура вычислительного устройства для реализации параллельной нулевизации в расширенном поле GF(24). При этом аппаратурные затраты будут определяться выражением
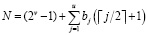. (10)
где bj – количество j-входовых сумматоров по модулю два, используемых в устройстве;
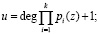
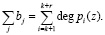
Оценим эффективность представленного метода определения местоположения и глубины ошибки, используя выражение (10). В качестве базового элемента выбираем нейроподобный многовходовой сумматор по модулю два. В таблице 3 приведены данные о затратах оборудования, выраженные в количестве формальных нейронов для различных диапазонов полей Галуа.
Таблица 3
Количество базисных элементов устройства
|
Количество сумматоров |
Разрядность сумматоров |
GF(23) |
GF(24) |
GF(25) |
|
2 |
1 |
|||
|
3 |
1 |
|||
|
4 |
2 |
3 |
||
|
5 |
2 |
|||
|
6 |
2 |
|||
|
8 |
8 |
|||
|
10 |
1 |
|||
|
14 |
1 |
|||
|
Количество нейронов |
8 |
25 |
54 |
|
|
Количество нейронов с учетом первого слоя |
15 |
40 |
85 |
На рисунке приведена вероятность безотказной работы устройств, реализующих процедуры последовательной и параллельной нулевизации в полиномиальной системе класса вычетов для полей Галуа GF(25).
Из представленного рисунка наглядно видно, что применение метода параллельной нулевизации позволяет сократить аппаратурные затраты необходимые на реализации процедур поиска и локализации в модулярных кодах по сравнению с ранее известным методом последовательной нулевизации. Очевидно, что снижение аппаратурных затрат обеспечивает более надежную работу всего параллельного вычислительного устройства. При этом, очевидно, что с увеличением разрядности обрабатываемых данных эффективность применения метода параллельной нулевизации возрастает. Кроме того, реализация процедуры параллельной нулевизации позволяет осуществить операцию поиска и локализации ошибок всего за одну итерацию, в то время как скорость выполнения последовательной нулевизации обратно пропорциональна количеству рабочих оснований ПСКВ. Таким образом, очевидно, что разработанный метод вычисления позиционной характеристики характеризуется довольно высокой надежностью работы при сравнительно небольших временных затратах на реализацию процедур поиска и определения местоположения ошибочных разрядов.
Выводы. В работе рассмотрены вопросы построения корректирующих кодов полиномиальной системы классов вычетов. Показано, что для выполнения этих операций в код ПСКВ надо вводить контрольные основания. Так введение двух избыточных модулей позволяет исправить все однократные ошибки. В статье приведен усовершенствованный алгоритм вычисления позиционной характеристики след полинома. Применение псевдоортогональных базисов в качестве констант нулевизации позволяет сократить временные и схемные затраты необходимые на вычисление этой позиционной характеристики.
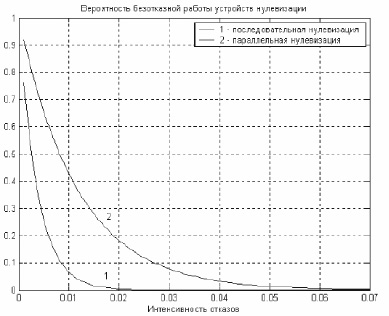
Вероятность безотказной работы устройств для GF(25)
Библиографическая ссылка
Мартиросян А.Г., Калмыков М.И. УСОВЕРШЕНСТВОВАННЫЙ АЛГОРИТМ НУЛЕВИЗАЦИИ В МОДУЛЯРНЫХ ПОЛИНОМИАЛЬНЫХ КОДАХ // Современные наукоемкие технологии. – 2014. – № 9. – С. 27-32;URL: https://top-technologies.ru/ru/article/view?id=34699 (дата обращения: 21.11.2024).