По результатам исследования, причиной аварии Чернобыльской АЭС явилось нарушение персоналом инструкций по управлению реактором, наложившиееся на конструктивные недостатки реактора. Реактор находился в конце рабочей компании его активной зоны, поэтому в ней накопилось максимальное количество радиоактивных продуктов деления и активации – 150 Ки.
Интенсивные выбросы из разрушенного реактора в окружающую среду радиоактивных веществ продолжались в течение 10 суток [1]. Выброшенные из активной зоны реактора в атмосферу радиоактивные продукты деления и радиоактивного топлива были разнесены воздушными потоками на сотни и тысячи километров, приведя к радиоактивному загрязнению территорий и оказав негативное воздействие на окружающую среду и здоровье проживающего на них населения. В наибольшей степени радиоактивному загрязнению подверглись территории России, Белоруссии и Украины (рис. 1).
Применительно к техногенному воздействию, заключающемуся в радиоактивном загрязнении, изменение экологического состояния ландшафта в упрощенном виде можно описывается системой дифференциальных уравнений вида:
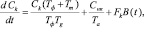 (1)
(1)
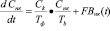 , (2)
, (2)
где 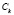 ,
, 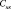 – уровень загрязнения почв ландшафта компенсируемыми и некомпенсируемыми вредными веществами;
– уровень загрязнения почв ландшафта компенсируемыми и некомпенсируемыми вредными веществами; 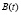 – интенсивность техногенного загрязнения;
– интенсивность техногенного загрязнения; 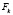 ,
, 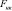 – доля воздействия, приходящаяся на загрязнение компенсируемыми и некомпенсируемыми веществами, соответственно;
– доля воздействия, приходящаяся на загрязнение компенсируемыми и некомпенсируемыми веществами, соответственно; 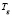 – характерное время процесса компенсации;
– характерное время процесса компенсации; 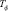 ,
, 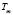 – соответственно, характерное время преобразования компенсируемой части в некомпенсируемую и обратно.
– соответственно, характерное время преобразования компенсируемой части в некомпенсируемую и обратно.
Решение системы уравнений (1-2) записывается в виде:
С = 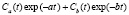 , (3)
, (3)
где 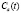 =fa
=fa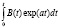 ;
; 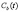 =fb
=fb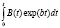 ;
;
a и b – корни характеристического уравнения рассматриваемой системы уравнений; f a, fb – константы, зависящие от начального состояния ландшафта.

Рис. 1. Мемориал погибшим ликвидатором на ЧАЭС
Заметим, что значения величин а и b зависят от геохимического типа ландшафта, характера техногенного воздействия, а также других факторов. Важен физический смысл их обратных величин, состоящий в том, что они представляют собой, соответственно, время реакции ландшафта на техногенные воздействия Ta = 1/a и время восстановления после снятия техногенной нагрузки Tb = 1/b. В реальных условиях обычно: Ta >> Tb.
Указанные величины имеют важное практическое значение при оценке необходимого объема и содержания работ при ликвидации долгосрочных экологических последствий техногенных аварий и катастроф. Однако на этом их значение не ограничивается.
Дело в том, что все рассмотренные выше показатели и параметры могут быть использованы для оценки экологического риска. Эти показатели и параметры носят стохастический характер. Они являются функциями большого числа случайных величин. Например, показатели Симпсона и Шеннона зависят от случайных значений энергии, поступающей с пищей, затрат энергии на поддержание нормального уровня жизнедеятельности и т.д.
С учетом этого обстоятельства можно писать не о строгих значениях этих показателях, а о вероятности того, что в конкретных условиях те или иные их значения будут иметь место. Для определения такой вероятности необходимо знать функцию распределения случайной величины показателя [2].
В общем виде рассматриваемая вероятностная величина может быть записана в виде формулы
P = 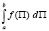 , (4)
, (4)
где 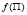 – функция распределения показателей Симпсона, Шеннона, Ta, Tb или иных вводимых в рассмотрение показателей. По физическому смыслу величина P выражает количественную меру соответствия состояния рассматриваемых элементов биосферы тому или иному экологическому состоянию.
– функция распределения показателей Симпсона, Шеннона, Ta, Tb или иных вводимых в рассмотрение показателей. По физическому смыслу величина P выражает количественную меру соответствия состояния рассматриваемых элементов биосферы тому или иному экологическому состоянию.
В том случае, когда рассматриваемая мера соответствует состоянию экологического неблагополучия, величина P приобретает физический смысл экологического риска.
Разработка практических методик требует тщательного выбора показателей и всестороннего обоснования их значений, за пределами которых возникает зона напряженной экологической ситуации или так называемая экологически проблемная зона [3], зона экологического бедствия или зона экологических катастроф. В таких зонах скорость антропогенных нарушений превышает темпы самосстановления природы и существует угроза коренного, но еще обратимого изменения природных систем. В зонах экологического бедствия происходит все более труднообратимая замена продуктивных экосистем менее продуктивными, ухудшаются показатели здоровья людей и т.д.. В зонах экологических катастроф происходит необратимый или весьма трудно обратимый переход к полной потере биологической продуктивности, возникновение опасности для жизни, здоровья, репродуктивной способности человека [4].
Библиографическая ссылка
Федоров А.Я., Мелентьева Т.А., Мелентьева М.А. ВОЗДЕЙСТВИЕ РАДИОАКТИВНЫХ ВЕЩЕСТВ НА ГЕОХИМИЧЕСКИЕ ЛАНДШАФТЫ // Современные наукоемкие технологии. 2014. № 6. С. 98-99;URL: https://top-technologies.ru/ru/article/view?id=34691 (дата обращения: 13.02.2026).



