Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Лучин И.В. 1 Кравченко И.Н. 1 Конкин М.Ю. 1 Золотов И.А. 1

---

1 ФГБВОУ ВПО «Военно-технический университет»

В настоящее время в нашей стране и за рубежом выпускается большое количество автомобильных шин различных модификаций с металлокордом в каркасе и брекере, причем, в зависимости от назначения шин слойность их металлокордного брекера, его размеры по ширине, тип металлокорда в брекере и каркасе могут быть самыми разными. Поэтому и энергосиловые характеристики процесса измельчения разных шин будут разные. В связи с этим возникает необходимость разработки теоретических методов расчета этих характеристик, поскольку организация и проведение экспериментальных методов их определения требуют больших затрат времени и труда, а ассортимент выпускаемых шин непрерывно расширяется.

Статья в формате PDF

896 KB

автомобильные шины

моделирование

утилизация

процесс разрезания

переработка

измельчение

1. Кравченко И.Н. Анализ системы переработки и рециклинга утилизируемой техники в России и зарубежом / И.Н. Кравченко, И.А. Золотов, И.В. Лучин // Научно-технический сборник: Вып. №23. – Балашиха: ВТУ при Спецстрое России, 2012. – С. 115 – 119.

2. Кравченко И.Н. Исследования процесса абразивного измельчения изношенных автомобильных шин при утилизации / И.Н. Кравченко, И.В. Лучин, А.Л. Чернуха // Научно-технический сборник, выпуск № 25. – Балашиха: ВТУ, 2014. – С. 80-84.

3. Патент № 139646, Российская Федерация, МПК В29В 17/00. Устройство для разрезания покрышек / И.Н. Кравченко, И.В. Лучин, И.А. Золотов и др.; заявитель и патентообладатель ФГБВОУ ВПО «Военно-технический университет» МО РФ (RU). – 2013151270/05; заявл. 19.11.2013; опубл. 20.04.2014. – Бюл. № 11.

4. Плотников Р.С. Дисковое ножевое устройство для разрезания // Трение и смазка в машинах и механизмах. – 2010. – №1. – С. 43-45.

5. Плотников Р.С. Разработка процессов и оборудования для разрезания изношенных автопокрышек с целью их утилизации: дис…канд. техн. наук. – Ярославль, 2007. – 126 с.

Наиболее сложным процессом предварительной переработки изношенных металлокордных автомобильных шин является разрезание протекторных браслетов (брекерных слоев), так как они содержат наибольшее количество металлокордных слоев [1, 5]. Схема разрезания протекторных браслетов показана на рис. 1.

В общем случае в состав протекторных браслетов входят наружный резиновый массив, защитный (экранирующий) слой текстильного обрезиненного корда, несколько брекерных слоев обрезиненного металлокорда, слой каркаса из обрезиненного металлокорда и внутренний резиновый слой (гермослой). Боковины металлокордных шин обычно состоят из одного слоя обрезиненного металлокорда и резинового массива [3, 4].

Бортовые части грузовых шин (вблизи бортовых колец) в общем случае содержат два слоя каркасного обрезиненного металлокорда (с учетом его заворота вокруг бортового кольца), резиновый наполнительный шнур, бортовую ленту из обрезиненного металлокорда, наружный резиновый массив. Из сказанного следует, что наиболее трудоемким для разрезания являются протекторные браслеты, поскольку в нем содержание металлокорда наибольшее [2]. Поэтому целесообразно для него в первую очередь провести исследование процесса предварительного разре-
зания.

Учесть в полном объеме влияние всех разрезаемых слоев брекера (протекторных браслетов) на общее усилие разрезания достаточно сложно. Для этого необходимо знать, например, удельные силы разрезания различных каркасных, брекерных и протекторных резин, прочность связи различных резин с разными кордными нитями и некоторые другие факторы (например, температуру и предысторию изношенной шины) и их влияние на усилие разрезания [5]. Поэтому при разработке математической модели процесса переработки резинокордных систем необходимо выделить главные (основные) факторы, влияющие на общее усилие разрезания.

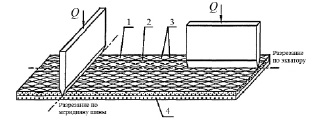
Рис. 1. Схема разрезания протекторных браслетов:
1 – слой протекторной резины; 2 – защитный слой обрезиненного текстильного корда; 3 – слои резины, армированной металлическим кордом (обрезиненный металлокордный брекер); 4 – слой каркасной резины, армированной металлическим кордом (каркасный обрезиненный металлокорд)

Составим с учетом влияния на величину общего усилия разрезания слоев текстильного и металлического корда расчетную схему процесса разрезания одного слоя корда протекторного браслета клинообразным ножом, причем разрез будем осуществлять вдоль меридиана, то есть поперек брекера (рис. 2).

Рассмотрим участок ширины l. Нить корда расположена под углом α к режущей кромке ножа ML. Угол заточки лезвия ножа составляет величину βн.

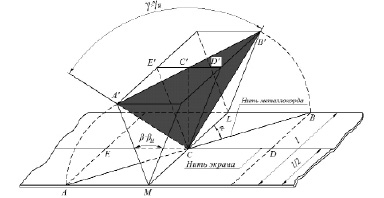
Рис. 2. Схема разрезания слоя металлокордного брекера:
l – ширина слоя, ML – режущая кромка ножа, α – угол расположения нити корда к режущей кромке ножа, β – угол перегиба слоя, βн – угол заточки лезвия ножа; γ – угол перегиба нити;
γн – угол заточки ножа в плоскости А’СВ’ нити

Рассматриваемый механизм процесса разрезания следующий: при внедрении клинообразного ножа в протекторный браслет в процессе взаимодействия ножа и слоя обрезиненного металлокорда последний будет перегибаться относительно кромки ножа ML. Допустим, что ширина слоя l при перегибе не изменяется (l = const). Тогда нити корда рассматриваемого слоя, в том числе нить АВ, после перегиба (на малом расстоянии от кромки ножа) в предельном случае будут прилегать к боковым граням лезвия ножа (прямые СВ’ и СА’). Точки А и В займут положение А’В’ соответственно. При этом угол перегиба нити γ (угол между линиями СА’ и СВ’) будет наименьшим из возможных (равным углу заточки ножа γн в плоскости нити А’СВ’), а угол перегиба слоя β будет равен углу заточки ножа βн. В этом предельном случае (рис. 3) усилие сопротивления рассматриваемой кордной нити внедрению ножа в протекторный браслет Q1н будет наибольшим, согласно уравнению равновесия системы «нож – кордная нить»:

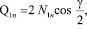(1)

где 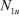 – усилие растяжения одной нити корда слоя.

Из геометрических построений (см. рис. 2) следует

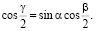(2)

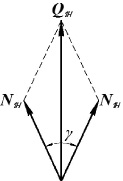
Рис. 3. Усилие сопротивления кордной нити внедрению ножа:
Q1н – усилие сопротивления рассматриваемой кордной нити внедрению ножа; N1н – усилие растяжения одной нити корда слоя; γ – угол перегиба нити

Используя зависимости (1) и (2), получим выражение для расчета усилия Q сопротивления всех нитей слоя внедрению ножа в металлокордный брекер

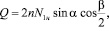(3)

где 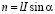 – число нитей слоя корда, пересекаемых линией разрезания; l – длина линии разреза слоя (ширина слоя брекера); I – частота нитей корда в слое, шт./длину.

Если величина усилия натяжения кордных нитей N1н (см. рис. 3) достигает своего предельного значения 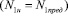, то произойдет разрыв всех нитей и рассечение данного слоя. В этом случае усилие прорезания слоя Qp определим из уравнения

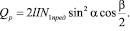(4)

Необходимо отметить, что N1н может достигнуть своего предельного значения 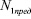раньше, чем нить коснется боковых поверхностей лезвия ножа, то есть при фактическом значении угла β большем, чем βн. Фактическая величина угла перегиба слоя корда β может находиться в пределах
βн < β < 180°. При этом, как видим из уравнения (4), при увеличении угла β усилие прорезания Qp будет уменьшаться и при β приближающемся к 180° будет приближаться к нулю. Максимальное усилие прорезания возникает при β = βн.

Полное максимальное усилие сопротивления всех слоев корда внедрению ножа Q∑ будет равно:

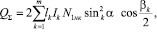(5)

где 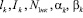 – соответственно, длина линии разреза слоя, частота нитей корда в слое, усилие натяжения нити, угол наклона нити, угол перегиба для k-го слоя металлокорда; m – количество слоев корда.

Полученное уравнение можно использовать, когда длина линии разреза (ширина слоев) разная. Если все слои имеют одинаковую длину l, то уравнение (5) можно представить в следующей форме

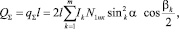(6)

или

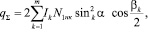(7)

где 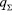 – суммарная удельная сила сопротивления многослойного материала.

Полученные зависимости (6) и (7) справедливы для общего случая разрезания протекторных браслетов (металлокордных брекеров) под любым произвольным углом.

Проанализируем уравнение (7) применительно к различным слоям протекторных браслетов.

При резании протекторных браслетов по меридиану линию разреза будут пересекать нити корда следующих слоев:

– экранирующих брекерных слоев, для которых αk = 90°;

– основных слоев металлокорда, для которых αk = ± 70°;

– каркасных слоев, для которых αk≈0°.

Для экранирующих слоев протекторных браслетов при разрезании по меридиану при αk= 90° имеем

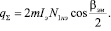(8)

Для двух слоев брекера (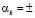70)

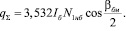(9)

Для каркасных слоев ()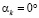

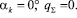(10)

Необходимо отметить, что нити корда каркаса не рассекаются, так как их направление близко к линии разреза. Следовательно, эти слои при разрезании по меридиану можно не учитывать.

Составим уравнение для расчета удельной силы разрезания вдоль протекторных браслетов.

В этом случае направление нитей экранирующих слоев близко к линии разреза и они практически не рассекаются ножом.

Наоборот, нити корда каркаса направлены перпендикулярно линии разреза и потому перерезаются.

При разрезании вдоль протекторных браслетов угол наклона нитей по отношению к режущей кромке ножа составит
αk= 90°αmk, где αmk – угол наклона нитей по отношению к меридиану шины.

Тогда из уравнения (5) получим

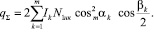(11)

Для двух слоев брекера ()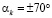

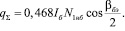(12)

Для точного решения уравнений (11) и (12) необходимо знать фактические значения натяжения кордных нитей в каждом слое в один и тот же момент времени, а также и углы перегиба этих слоев корда, определить которые достаточно трудно. Поэтому рекомендуется следующий подход для оценки максимально возможного усилия разрезания ().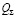

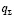Нити корда слоев экрана, брекера и каркаса находятся вблизи друг от друга. Так как за счет межслойного перекрещивания нити образуют жесткую структуру и взаимодействуют при разрезании протекторных браслетов, вводим следующие допущения:

1. Разрыв всех нитей происходит одновременно, когда натяжение кордных нитей в каждом слое достигает своего предельного значения <<luchin24.wmf>> (оно приводится в технической документации на корд).

2. Разные слои протекторных браслетов в момент разрезания имеют один и тот же средний угол перегиба βср.

Рассчитаем значения угла βср по формуле

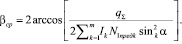(13)

Проделав эту процедуру для большого круга протекторных браслетов, можно установить наиболее вероятные значения этих углов. Результаты полученных авторами расчетов представлены в таблице.

Из табл. 1 следует, что значения βср укладываются в небольшой диапазон от 141,5° до 161,8°. Это позволяет сделать вывод, что βср можно считать параметром уравнений (5)-(7) и в дальнейшем использовать его для прогнозирования усилий резания протекторных браслетов любых конструкций (при одном и том же угле заточки ножа).

Значения удельной силы разрезания и средних углов перегиба слоев протекторных браслетов

Учитывая, что максимальное усилие разрезания получается при меньшем βср, а экспериментальный угол перегиба слоев для всех исследованных шин превышает 140°, рекомендуется в расчетах шин с посадочным диаметром 13», 14», 15» принимать угол перегиба βср равным 140°.

Выводы

1. Физические процессы, протекающие при переработке изношенных автомобильных шин, в значительной степени отличаются от процессов, протекающих при разрезании твердых материалов. Существующие методы анализа и прогноза результатов разрезания изношенных шин в основном ориентированы на материалы, сохраняющие свои упругопластические свойства в узких пределах возможных деформаций, так как шины способны сохранять такие свойства при значительно больших деформация и переходить из неравновесного состояния в равновесное в процессе релаксации, поэтому такие методы к исследуемым процессам неприменимы.

2. Полученные расчетные данные являются на сегодняшний день актуальными, поскольку позволяют обоснованно производить выбор рациональных вариантов перерабатывающего оборудования с учетом конструктивных особенностей, рассчитывать его производительность и энергосиловые характеристики, а также проектировать и разрабатывать технологические процессы утилизации изношенных автомобильных шин и резинотехнических изделий.

Библиографическая ссылка