Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Гапочкин А.В. 1 Калмыков М.И. 1 Васильев П.С. 1

---

1 ФГАОУ ВПО «Северо-кавказский федеральный университет»

Современные средства цифровой обработки сигналов должны обеспечивать первичную обработку сигнала в реальном масштабе времени. Распараллеливание на уровне арифметических операций позволяет обеспечить данное требование. При этом использование алгебраических кодов, обладающих свойством кольца, позволяет проводить с высокой эффективностью операции по обнаружения и коррекцию ошибок. Так как данные коды относятся к кодам классов вычетов, то для организации коррекции результата должны быть использованы позиционные характеристики. В работе представлены модификации алгоритма вычисления интервального номера..

Статья в формате PDF

957 KB

коды классов вычетов

система остаточных классов

обнаружение и коррекция ошибок

позиционные характеристики

интервальный номер

1. Бережной В.В., Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Шилов А.А. Нейросетевая реализация в полиномиальной системе классов вычетов операций ЦОС повышенной разрядности // Нейрокомпьютеры: разработка и применение. – 2004. – № 5-6. – С. 94.

2. Червяков Н.И., Сахнюк П.А., Шапошников А.В., Ряднов С.А. Модулярные параллельные вычислительные структуры нейросетевых систем. – М.: Физматлит., 2003. – 303 с.

3. Калмыков И.А., Оленев А.А., Бережной В.В. Систолический процессор дискретного преобразования Фурье с коррекцией ошибки // Патент на изобретение RUS 2018950

4. Чипига А.Ф., Калмыков И.А. Структура нейронной сети для реализации цифровой обработки сигналов повышенной разрядности // Наука. Инновации. Технологии. – 2004. – Т.38. – С. 46.

5. Устройство для преобразования числа из полиномиальной системы классов вычетов в позиционный код с коррекцией ошибки // Калмыков И.А., Петлеванный С.В., Сагдеев А.К., Емарлукова Я.В. // Патент России № 2309535. 31.03.2006. Бюл. № 30 от 27.10.2007.

6. Калмыков И.А., Червяков Н.И., Щелкунова Ю.О., Шилов А.А., Бережной В.В Архитектура отказоустойчивой нейронной сети для цифровой обработки сигналов// Нейрокомпьютеры: разработка и применение. – 2004. – № 12. – С. 51-57.

7. Калмыков И.А., Хайватов А.Б., Сагдеев А.К. Разработка методов обнаружения и коррекции ошибок в коде полиномиальной системы классов вычетов, базирующихся на вычислении синдрома ошибки // Фундаментальные исследования. – 2006. – №2. – С. 13.

8. Калмыков И.А., Зиновьев А.В., Емарлукова Я.В., Высокоскоростные систолические отказоустойчивые процессоры цифровой обработки сигналов для инфотелекоммуникационных систем // Инфокоммуникационные технологии. Самара. – 2009. – №2. – С. 31-37/

9. Калмыков И.А., Резеньков Д.Н., Тимошенко Л.И. Непозиционное кодирование информации в конечных полях для отказоустойчивых спецпроцессоров цифровой обработки сигналов// Инфокоммуникационные технологии. – 2007. – Т.5. – №3. – С.36-39.

10. Калмыков И.А., Лисицын А.В., Гахов В.Р. Алгоритм обнаружения и коррекции ошибок в модулярном коде на основе вычисления интервального номера полинома// Фундаментальные исследования. – 2006. – №2. – С. 12.

Для обеспечения реального масштаба времени при реализации цифровой обработки сигналов (ЦОС) применяют параллельно-конвейерные вычисления. Одним из наиболее перспективных направлений обеспечения высокой скорости обработки сигналов является использование модулярных непозиционных кодов. В данных системах позиционные отсчеты сигналов представляются в виде наборов остатков, величины которых определяются значениями оснований кодов классов вычетов [1-4]. Наряду с высоким быстродействием непозиционные модулярные коды позволяют проводить операции по поиску и коррекции ошибок, которые возникают в процессе вычислительных устройств из-за отказов оборудования. Правильный выбор соответствующего алгоритма, позволяющего определить ошибочный остаток, а также глубину ошибки, позволить выполнить поиск и коррекцию ошибок при минимальных схемных и временных затратах.

Известно, что введение двух контрольных оснований в упорядоченное множество оснований системы остаточных классов (СОК), удовлетворяющих условию

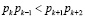, (1)

где k – количество рабочих оснований, позволяет осуществлять коррекцию однократных ошибок, возникающих в кодах СОК. Использование контрольных оснований расширяет рабочий диапазон, определяемый согласно

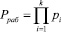, (2)

до значения полного диапазона

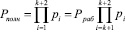. (3)

Комбинация СОК считается разрешенной, если она принадлежит рабочему диапазону. Известно, что ошибка преобразует правильную комбинацию 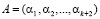в комбинацию 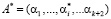, где 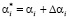 – искаженный остаток,
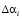– глубина ошибки. В этом случае перевод искаженного числа из рабочего диапазона, в диапазон полный. Следовательно, зная местоположение искаженной комбинации 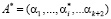, можно однозначно определить основание, по которому произошла ошибка, а также ее глубину.

Данное свойство непозиционных модулярных кодов и предопределило повышенный интерес разработчиков к позиционным характеристикам, с помощью которых можно однозначно определить ошибочное основание и глубину ошибки. В качестве позиционных характеристик могут выступать коэффициенты обобщенной полиадической системы (ОПС), приведенные в работах [5, 6]. В работах [7, 8] рассматриваются алгоритмы расширения системы оснований модулярного кода с последующим вычислением невязки кода. Особое место среди позиционных характеристик занимает – интервальный номер [9, 10]. Это обусловлено тем, что данная позиционная характеристика имеет простой физический смысл. Определение данной характеристики осуществляется согласно

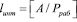. (4)

Очевидно, что операция деления (4) относится к немодульным, ее сводят к совокупности модульных операций. В работе [9] представлен алгоритм, который позволяет осуществлять поиск и коррекцию ошибки в коде классов вычетов, используя интервальный номер числа.

В основу данного алгоритма положено свойство подобия ортогональных базисов полной и безизбыточных систем класса, согласно которому

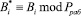, (5)

где Bi* и Bi – ортогональные базисы безизбыточной и полной системы.

Тогда, используя (5), получаем

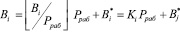. (6)

Подставив последнее равенство в выражение (4) получаем

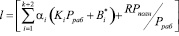. (7)

где R – ранг полной системы оснований СОК.

Проведя упрощения, имеем

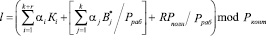, (8)

где .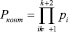

Так как множество значений интервального номера l представляет собой кольцо по модулю Pконт, то выражение (8) можно преобразовать к виду

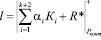, (9)

где 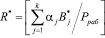 – ранг в безизбыточной системы.

Если число, представленное в модулярном коде принадлежит рабочему диапазону, то значение интервального номера равно нулю, т.е. l= 0. При возникновении ошибки числа А не будет принадлежать рабочему диапазону, а будет размещаться вне его. Следовательно, если номер числа будет отличен от нуля, то свидетельствует о том, что исходная комбинация модулярного числа содержит ошибку.

Рассмотрим пример применения данной позиционной характеристики. Пусть задана упорядоченная СОК с рабочими основаниями р1=2, р2=3, р3=5. В качестве контрольных оснований выберем основания р4=7 и р5=11. Тогда рабочий диапазон данной системы СОК будет равен Pраб= 30. При этом полный диапазон такой системы
Pполн= 2310. 

В данной полной системе основания ортогональные базисы равны

;

;

;

;

.

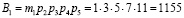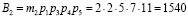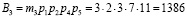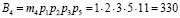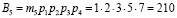Представим ортогональные базисы согласно (6)

;

;

;

;

.

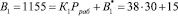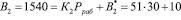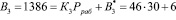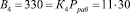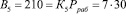Для данной системы СОК значение Pконт= 77

Пусть имеем число А = (0, 2, 2, 2, 2) = 2. Вычислим значение интервального номера для данного числа, используя разработанный алгоритм.

Вычислим значение ранг в безизбыточной системы, определяемые основаниями р1=2, р2=3, р3=5.

.

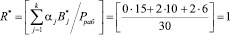Тогда значение интервального номера для данной комбинации

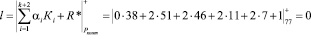
Полученный результат свидетельствует о том, что данная комбинация не содержит ошибки и относится к разрешенным.

Пусть ошибка произошла по первому основанию и ее глубина равна .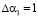
Тогда модулярный код имеет вид
А* = (1, 2, 2, 2, 2) = 2. Вычислим значение интервального номера для данного числа, используя разработанный алгоритм.

Вычислим значение ранг в безизбыточной системы, определяемые основаниями р1=2, р2=3, р3=5.

.

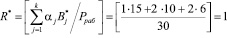Тогда значение интервального номера для данной комбинации

.

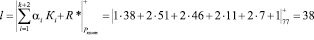Полученный результат свидетельствует о том, что данная комбинация содержит ошибку. В таблице приведены значения ошибок по основаниям модулярного кода и соответствующие им номера интер-
валов.

Распределение однократных ошибок кода СОК

Проведенный анализ необходимых схемных затрат на реализацию данного алгоритма вычисления позиционной характеристики показал, что применение составного модуля Ркоит, по которому определяется значение интервального номера l, с точки зрения аппаратурных затрат, является не самым оптимальным. Это обусловлено тем, что одномерные исчисления над кольцом, определяемым значением ,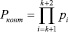
требует обработки 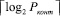разрядных операндов.

С целью сокращения аппаратурных затрат в работе предлагается усовершенствовать данный алгоритм. В основу усовершенствования целесообразно положить изоморфизм, порожденный китайской теореме об остатках (КТО). Использование этого изоморфизма позволяет перейти от одномерной обработки к многомерной. Приравнивая соответствующие значения Рконт и оснований 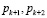, получаем 2 преобразования, которые можно реализовать параллельно

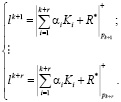(10)

Рассмотрим пример. Пусть имеем число А = (0, 2, 2, 2, 2) = 2. Вычислим значение интервального номера для данного числа, используя разработанный алгоритм, задаваемый выражением (10).

Как и ранее, вычисленное значение ранг в безизбыточной системы, определяемые основаниями р1=2, р2=3, р3= 5 будет определяться

.

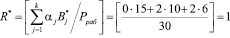Тогда значение интервального номера для данной комбинации будет вычислено с помощью алгоритма (10)

Таким образом, интервальный номер
l = (0, 0). Это соответствует ситуации, когда модулярный код не содержит ошибки.

Пусть ошибка произошла по первому основанию и ее глубина равна 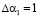. Тогда модулярный код имеет вид
А* = (1, 2, 2, 2, 2) = 2. Вычислим значение интервального номера для данного числа, используя разработанный алгоритм.

Вычислим значение ранг в безизбыточной системы, определяемые основаниями р1=2, р2=3, р3=5.

.

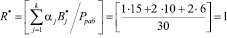Тогда значение интервального номера для данной комбинации

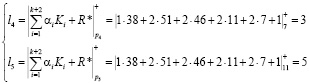
Полученный результат отличен от нуля. Это свидетельствует о том, что данная комбинация содержит ошибку. В этом случае, для оснований р4=7, р5=11 полученный интервал, определяемый остатками l = (3, 5), будет равен

,

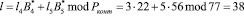где 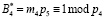– ортогональный базис по первому контрольному основанию р4 = 7; 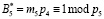– ортогональный базис по второму контрольному основанию р5 = 11. 

Несмотря та то, что выражения (9) и (10) позволяют получить одинаковый результат, тем не менее, использование изоморфизма КТО позволяет сократить схемные затраты, которые необходимы на реализацию алгоритма вычисления интервала. Проведенный анализ показал, что реализация вычисления интервала согласно (10) потребовала на 14,3 % меньше схемных затрат по сравнению с алгоритмом (9). При этом при увеличении размерности контрольных оснований выигрыш в схемных затратах увеличивается.

Выводы

Использование избыточных модулярных кодов позволяет осуществлять поиск и коррекцию ошибок, которые могут возникать в процессе функционирования непозиционного спецпроцессора. Рассмотрен алгоритм, позволяющий определить местоположение ошибки и ее глубину с использованием позиционной характеристики интервал. Для снижения схемных затрат был разработан новый алгоритм, в основу которого был положен изоморфизм китайской теоремы об остатках. Проведенные исследования показали, что переход к параллельному алгоритму позволил сократить схемные затраты, необходимые для вычисления позиционной характеристики при обработке 16-разрядных данных на 14,3 % по сравнению с классическим методом вычисления интервала числа. При этом при увеличении размерности контрольных оснований возрастает выигрыш от использования разработанного алгоритма.

Библиографическая ссылка