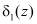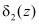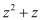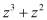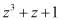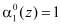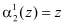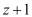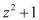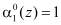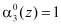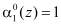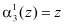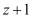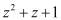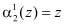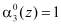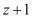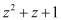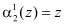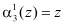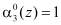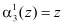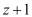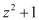Применение методов цифровой обработки, которые характеризуются обработкой значительных объемов информации в реальном масштабе времени, делает целесообразным разработку специализированных процессоров (СП) для их решения. Для обеспечения высокой скорости обработки данных в работах [1, 2] предлагается использовать модулярные арифметические системы. Применение данных систем позволяет повысить скорость выполнения операций сложения, вычисления и умножения по модулю за счет распараллеливания на уровне операций. Очевидно, что усложнение структуры СП ЦОС приводит к увеличению числа отказов, возникающих во время работы вычислительных устройств. Для решения данной проблемы необходимо разработать алгоритм поиска и коррекции ошибок, который позволил бы обнаруживать и корректировать ошибки, которые возникают в процессе функционирования непозиционного СП ЦОС. При этом данный алгоритм должен обеспечивать максимальную корректирующую способность.
Постановка задачи исследований
В настоящее время модулярные арифметические модулярные системы нашли широкое применение в различных сферах, связанных с информационными технологиями. В работах [1-4] доказана целесообразность использования модулярных кодов при реализации методов цифровой обработки сигналов. Широкое применение модулярные алгебраические системы нашли в сфере обеспечения защиты информации от несанкционированного доступа (НСД). Так в работах [5, 6] показана возможность применения модулярной арифметики в криптографических системах, использующих полиномиальную систему классов вычетов. В работе [7] рассмотрены вопросы использования модулярной псевдослучайной функции повышенной эффективности в электронных коммерческих системах. Использование модулярных алгебраических структур позволяет обеспечить требуемый уровень защиты информации от НСД.
Кроме отмеченных выше сфер применения, модулярные алгебраические системы целесообразно использовать для реализации операций поиска и коррекции ошибок, возникающих в процессе функционирования непозиционных спецпроцессоров. Так в работах [8-10] приведены алгоритмы, которые позволяют провести обнаружение и коррекцию ошибок в полиномиальной системе классов вычетов. Основным недостатком данных систем, является то, что при наличии двух контрольных оснований ПСКВ система способна исправлять только однократные ошибки. В работе предлагается алгоритм, позволяющий повысить корректирующие способности полиномиальных кодов.
В полиномиальной системе классов вычетов в качестве оснований системы используются неприводимые полиномы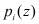 
, где 
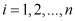. В этом случае любой полином 
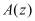, удовлетворяющий условию
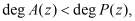(1)
где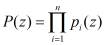 
– рабочий диапазон системы, 
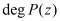– степень полинома, можно однозначно представить в виде набора остатков
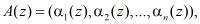(2)
где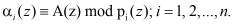 
Для реализации процесса обнаружения и исправления ошибок в модулярном коде полинома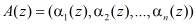 
вводят избыточность. С этой целью выбирается одно контрольное основание 
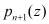, удовлетворяющее условию
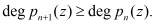(3)
В прототипе доказано, что используя данное контрольное основание для вычисления двух проверочных остатков
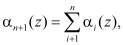(4)
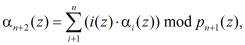(5)
где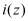 
– полиномиальная форма i-го порядкового номера, 
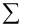– суммирование по модулю два, можно однозначно исправить однократную ошибку.
Под однократной ошибкой понимается искажение одного разряда в кодовой комбинации, представленной равенством (2).
При работе данное устройство обрабатывает n информационных остатка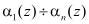 
и два контрольных остатка 
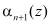и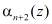 
.
Для обнаружения ошибки в переданной кодовой комбинации вычисляются значения
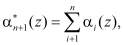(6)
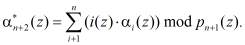(7)
Полученные значения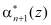 
и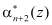 
используются для вычисления синдрома ошибки согласно
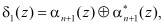(8)
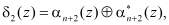(9)
где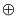 
– суммирование по модулю два.
Если синдром ошибк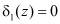и 
и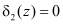 
, то данная комбинация не содержит ошибки. В противном случае, когда 
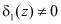и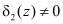 
, принятая комбинация является запрещенной, т.е. ошибочной. По величине 
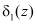и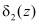 
можно провести коррекцию однократной ошибки.
В табл. 1 приведены значения синдромов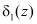 
и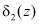 
, а также соответствующие им константы ошибки для рабочих оснований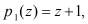 
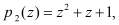
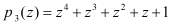и контрольного основания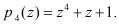 
Таблица 1
Синдромы ошибки в коде ПСКВ
|
|
|
константа ошибки ∆конст |
|
0 |
0 |
(0, 0, 0, 0, 0) |
|
1 |
1 |
(1, 0, 0, 0, 0) |
|
1 |
z |
(0, 1, 0, 0, 0) |
|
z |
z2 |
(0, z, 0, 0, 0) |
|
1 |
z+1 |
(0, 0, 1, 0, 0) |
|
z |
|
(0, 0, z, 0, 0) |
|
z2 |
|
(0, 0, z2, 0, 0) |
|
z3 |
|
(0, 0, z3, 0, 0) |
Однако, используя два контрольных остатка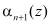 
и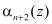 
, можно исправить и двукратные ошибки, т.е. ошибки, произошедшие в двух разрядах комбинации 
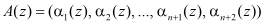одновременно.
В табл. 2 приведены значения синдромов ошибк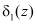и 
и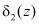 
при всех возможных двукратных ошибках по рабочим основаниям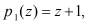 
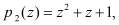
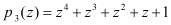, в которых произошла коллизия, т.е. совпадение.
Таблица 2
Коллизии при двукратных ошибках в коде ПСКВ
|
№ п/п |
Отказавший разряд 1-го основания |
Отказавший разряд 2-го основания |
δ1 |
δ2 |
∆ кор |
|
1 |
|
|
|
|
коллизия |
|
2 |
|
|
0 |
z |
коллизия |
|
3 |
|
|
|
|
коллизия |
|
4 |
|
|
|
|
коллизия |
|
5 |
|
|
0 |
z |
коллизия |
|
6 |
|
|
|
|
коллизия |
Проведенный анализ табл. 2 показывает, что совпадение пар значени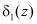й 
и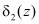 
не произошло, за исключением совпадения строк 1 и 4, 2 и 5, 3 и 6. Это означает, что устройство способно корректировать двукратные ошибки за исключением отмеченных совпадающих строк.
Чтобы обеспечить процедуру коррекции результата в условиях коллизии (совпадение синдрома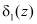 
и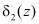 
) в устройство введены блок управления, второй блок памяти, блок устранения коллизии.
Функциональная схема устройства представлена на рис. 1. Она включает: регистр 1, вход 2, блок устранения коллизии 3, модуль вычисления синдрома ошибки 4, содержащий первый блок вычисления ошибки 5, второй блок вычисления синдрома ошибки 6, блок управления 7, первый блок памяти 8, второй блок памяти 9, сумматор 10, выход устройства 11.
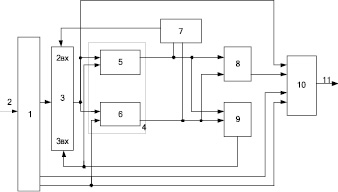
Рис. 1. Функциональная схема устройства, позволяющего увеличить корректирующие способности кодов ПСКВ
Устройство работает следующим образом: на вход 2 устройства поступает модулярный код полинома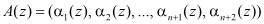 
. Контролируемая комбинация записывается в регистр 1. На первый вход блока 3 устранения коллизии с первого выхода регистра 1 поступает значение 
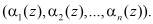Если коллизия не обнаружена блоком управления 7, то на второй вход блока 3 поступает управляющая комбинация y=0. Одновременно с выхода второго блока 9 памяти на третий вход блока 3 устранения коллизии поступает четырехразрядная комбинация 
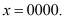Благодаря этому входная комбинация не изменяется и с выхода блока 3 устранения коллизии подается на первый вход первого блока 5 и второго блока 6 вычисления синдрома ошибки, входящих в состав модуля 4 вычисления синдрома ошибки, а также на первый вход сумматора 10.
На второй вход первого блока 5 вычисления синдрома ошибки подается с второго выхода регистра 1 значение первого контрольного остатка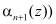 
. Блок 5 реализует выражение (8).
На второй вход второго блока 6 вычисления синдрома ошибки подается с третьего выхода регистра 1 значение второго контрольного остатка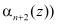 
. Данный блок 6 реализует выражение (9).
Величины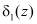 
и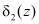 
в двоичном коде поступают на соответствующие входы первого 8 и второго 9 блоков памяти и блок управления 7.
Если коллизия отсутствует, а это соответствует условию, когда контролируемая комбинация
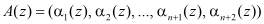
не содержит ошибки или имеет однократную ошибку или двухкратную, за исключением когда ошибка одновременно произошла в комбинациях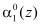 
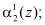
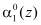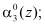
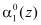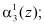
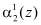и 
и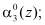 
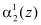и 
и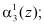 
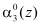и 
и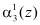 
, где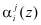 
– j-й разряд i-го канала, то с выхода блока управления 7 поступает управляющий сигнал 
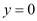на второй вход блока 3 устранения коллизии.
Если однократная ошибка произошла в нулевом разряде первого основания, в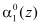 
т. е. когда значение синдрома ошибк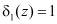и 
и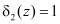 
, то с выхода второго блока 9 памяти снимается комбинация x=1000 которая подается на третий вход блока 3 устранения коллизии.
Если однократная ошибка произошла в первом разряде второго основания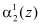 
, т. е. когда значение синдрома ошибк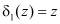и 
и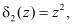 
то с выхода второго блока 9 памяти подается на третий вход блока 3 устранения коллизии комбинация x=0100.
Если однократная ошибка произошла в нулевом разряде третьего основания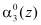 
, то есть когда значение синдрома ошибк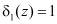и 
и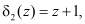 
то с выхода второго блока 9 памяти подается на третий вход блока 3 устранения коллизии комбинация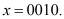 
Если однократная ошибка произошла в первом разряде третьего основания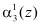 
, т. е. когда значение синдрома ошибк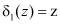и 
и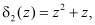 
то с выхода второго блока 9 памяти подается на третий вход блока 3 устранения коллизии комбинация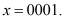 
В зависимости от величины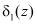 
и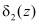 
с выхода первого блока 8 памяти выдается соответствующая константа ошибки ∆конс. Это значение поступает в сумматор 10, где суммируется со значением комбинации 
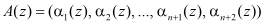, которая подается в параллельном коде на первый, третий и четвертый входы сумматора 10. Исправленное значение A(z) с выхода сумматора 10 подается на выход 11 устройства.
При возникновении коллизии, это соответствует ситуации, когда с выходов блоков 5 и 6 вычисления синдрома ошибки подаются значения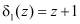 
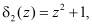
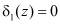и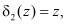 
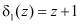и 
и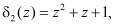 
то с выхода блока управления 7 на второй вход блока 3 поступает управляющий сигнал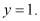 
В результате контролируемая комбинация модулярного кода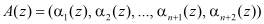 
будет содержать только однократную ошибку. Эта ошибка будет обнаружена в модуле 4 вычисления синдрома по значениям 
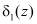и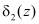 
. Эти значения подаются на входы первого блока 8 памяти, с выхода которого выдается ∆кор, что позволяет исправить вторую ошибку в контролируемой комбинации.
Проведенные исследования показали, что предлагаемый алгоритм работы устройства позволяет повысить корректирующие способности кода ПСКВ с двумя контрольными основаниями.
Вывод. Использование модулярного полиномиального кода позволяет не только повысить скорость выполняемых вычислений, но и проводить процедуры поиска и коррекции ошибок, которые возникают в процессе работы спецпроцессоров. В ходе проведенных исследований был разработан алгоритм, позволяющий повысить корректирующие способности непозиционных кодов ПСКВ. Благодаря данному алгоритму избыточный код ПСКВ с двумя контрольными основаниями может исправлять все двукратные ошибки.
Библиографическая ссылка
Стрижков Н.С., Калмыков М.И. УВЕЛИЧЕНИЕ КОРРЕКТИРУЮЩИХ СПОСОБНОСТЕЙ МОДУЛЯРНОГО ПОЛИНОМИАЛЬНОГО КОДА // Современные наукоемкие технологии. – 2014. – № 8. – С. 40-44;URL: https://top-technologies.ru/ru/article/view?id=34622 (дата обращения: 21.11.2024).