Исследование интегрируемых обобщений модели ферромагнетика Гейзенберга (МГ) на основе теории солитонов является одним из приоритетных направлений в области нелинейной математической физики. В настоящее время активно исследуются не только (1+1)-мерные, но и (2+1)-мерные обобщения спиновой МГ, такие как уравнение Ишимори [1], уравнение Мырзакулова-I (М-I) [2]. В работах [2-6] изучены алгебро-геометрические аспекты обобщенных спиновых моделей, методом Хироты найдены их точные солитонные и солитоноподобные решения, которые находят применение в различных областях физики. В [7] построено преобразование Дарбу (ПД) для уравнения M-I и некоторые его решения. В данной работе предложен иной подход построения ПД для этого уравнения и получены солитонные решения, вызывающие очевидный интерес, поскольку они представляют чисто нелинейный эффект, и не имеют аналога в линейной теории диспергирующих систем.
Уравнение M-I имеет вид [2]
, (1а)
(1б)
где
- спиновая матрица, S2=I и trS=0, нижние индексы x, y, t, обозначают производные по соответствующим аргументам, [,] - коммутатор, и- скалярный потенциал.
Интегрируемость уравнения (1) ассоциируется с условием совместности пары Лакса:
(2)
Здесь матричные операторы U и V имеют вид
Далее построим ПД для уравнения (1) с учетом особенности его пары Лакса. Преобразуем пару Лакса (2) к виду
(3)
где
а 
Искомую матрицу N выберем как
и 
.
Из условии совместности системы уравнений (3) имеем
(4)
Сравнивая коэффициенты 
в первом уравнении (4), получаем
(5)
(6)
(7)
(8)
С другой стороны, из второго уравнения (4):
(9)
(10)
(11)
Очевидно, что для матрицы N будем иметь следующие уравнения:
(12а)
(12б)
(12в)
Теперь мы готовы написать ПД для уравнения M-I, связывающее его решение S с новым решением 
, и потенциал u c 
. Оно имеет вид
. (13)
Исходя из некоторых вычислений, элементы матрицы N можем представить в виде
(14)
Подставляя (14) в (13), получаем
(15а)
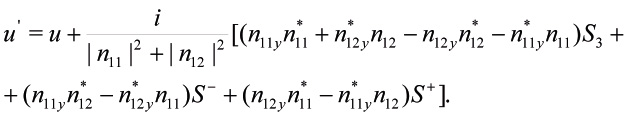(15б)
Теперь полагаем, что
(16)
где H - матрица следующего вида:
(17)
первый столбец которой является решением системы (2). Требуется определить второй столбец так, чтобы тот тоже являлся решением этой системы. Здесь det
, 
, где 
и 
- комплексные константы.
Не трудно убедиться, что
(18)
Из системы уравнений (12) с учетом (18) следует, что N удовлетворяет уравнениям
(19)
Отметим, что ограничения для S будут удовлетворены, если матричные решения системы (3) удовлетворяют условиям
(20)
которые следуют из системы уравнений
(21)
где 
обозначает эрмитово сопряжение. После некоторых вычислений получим формулы
(22)
(23)
где * обозначает комплексное сопряжение.
Собственные функции системы (3) выберем как 
, где 
Таким образом, элементы матрицы N определены в следующей форме:
(24)
Далее рассмотрим частный случай 
Тогда уравнение (15а) будет иметь вид
(25)
Теперь мы можем написать односолитонное решение уравнения (1) в следующем виде:
В итоге отметим, что для получения решения обобщенной спиновой модели (1) использован метод преобразования Дарбу. При этом сначала было построено само преобразование Дарбу для изучаемой модели. Решение уравнения (1б) для потенциала u’ также можно получить из уравнения (15б).
Библиографическая ссылка
Нугманова Г.Н., Жасыбаева М.Б., Мамырбекова Г.К. ПРЕОБРАЗОВАНИЕ ДАРБУ И ТОЧНЫЕ РЕШЕНИЯ ОДНОЙ ОБОБЩЕННОЙ СПИНОВОЙ МОДЕЛИ // Современные наукоемкие технологии. – 2014. – № 4. – С. 135-138;URL: https://top-technologies.ru/ru/article/view?id=34583 (дата обращения: 03.12.2024).