В условиях рыночной экономики каждый предприниматель сам решает, каким образом действовать, чтобы в сложившейся ситуации извлечь наибольшую прибыль. Интуитивные представления в данном случае не всегда могут являться верным ориентиром для принятия решений. Во многих случаях было бы рационально использовать математический подход для обоснования целесообразности принимаемых решений. В частности, многие экономические ситуации можно смоделировать и найти оптимальное решение с помощью методов математического программирования. В нашей статье мы рассмотрим задачу планирования инвестиций и применение метода Лагранжа для ее решения.
Предприниматель располагает свободным капиталом в размере 360 тысяч рублей. Исследования рынка показали, что наибольшую прибыль от вложения капитала можно получить при производстве изделий A и B. Инвестирование капитала может осуществляться в любых пропорциях. Однако вследствие различных причин (ограниченность спроса, специфика затрат на производство и т.п.) средняя прибыль в расчете на единицу произведенного товара не остается неизменной, а линейно снижается в зависимости от количества произведенной продукции: p1=100-q1. (где q1 є (0; 100)). Средняя прибыль на единицу продукта B также линейно зависит от объема производства и выражается формулой: p2=80-0,25q2, где q2 є (0; 320).
При этом анализ производственных возможностей показал, что вложения капитала в производство единицы продукции снижаются с увеличением объема производства. Средний расход на единицу продукции товара A линейно зависит от достигнутого уровня производства: y1=10-0,1x1 (справедливо для q1 є (0; 100)). А для товара B аналогичная зависимость имеет вид: y2=12-0,1х2. (при х2 є (0; 120)). Предпринимателю необходимо решить, как наиболее выгодно инвестировать имеющийся капитал в производство.
Как правило, зависимости между экономическими факторами лишь условно можно считать линейными. В основном, такие показатели, как прибыль, себестоимость, объем спроса и предложения, затраты на производство и др., в действительности изменяются непропорционально росту объема производства, поэтому для более адекватного моделирования реальных экономических процессов приходится применять зависимости более сложных видов [2]. Однако, несмотря на очевидную условность приведенных закономерностей, они в целом адекватно отражают специфику процесса.
Составим экономико-математическую модель планирования инвестиций в проекты производства A и B. Требуется максимизировать прибыль в условиях непостоянных затрат капитала на производство единицы продукции и получаемого дохода. Обозначим х1 - планируемый объем производства продукции А, х2 – планируемый объем производства продукции В. Тогда объем денежных средств, инвестируемых в производство A и B, будет задан соотношением: (10-0,1х1)х1 + (12-0,1 х2) х2.
Эта величина должна соответствовать объему всего имеющегося у предпринимателя капитала, то есть должно выполняться уравнение:
(10-0,1х1)х1 + (12-0,1х2)х2 =360,
или 10х1-0,1(х1)2 +12х2-0,1(х2)2 = 360.
В результате инвестирования в производство A и B предприниматель получает прибыль, которую модно рассчитать как произведение объема производства на среднее значение прибыли на единицу продукции. Тогда целевая функция задачи имеет вид: Z = (100-х1)*х1 + (80-0,25х2)* х2.
Требуется найти такие х1 є(0;100), х2 є (0;120), при которых целевая функция принимает максимальное значение. Таким образом, получена задача нелинейного программирования:
Z = (100-х1)*х1 + (80-0,25х2)* х2→max,
10х1-0,1(х1)2 +12х2-0,1(х2)2 = 360,
х1 є(0;100), х2 є (0;120).
Решим задачу методом множителей Лагранжа [1]. Составим функцию Лагранжа:
L(x1, x2, u) = 100x1-(x1)2 + 80x2-0, 25 (x2)2 + u (10x1-0, 1(x1)2 + 12x2-0, 1(x2)2 – 360)
Найдем частные производные функции Лагранжа:
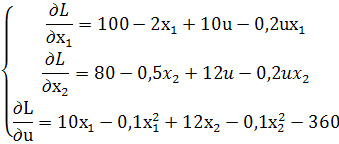
Приравняем частные производные к нулю и найдем стационарные точки.
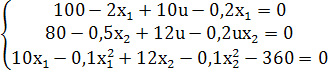
Выразим из первых двух уравнений х1 и х2 через u:
х1 = 100 +10u/2+0,2u; x2 = 80+12u/0, 5+0,2u
Полученные выражения подставим в третье уравнение и найдем значение u.

Дальнейшие вычисления вручную затруднительны, поэтому выполним их в программе Excel. Для решения уравнения используем функцию «подбор параметра». В результате вычислений получены два значения переменной u. Для первого значения u = -7,5 найдем соответствующие значения x1 = 50, x2 =10; при втором значении u ≈ 2,49 получим: x1 =50, x2 ≈ 110. Таким образом, с достаточной степенью точности найдены две стационарные точки: M(50, 10) и N(50, 110). Подставим получившиеся значения в целевую функцию и вычислим ее экстремумы: Z(M)=3275, Z(N)=8275. Следовательно, аксимальная прибыль, которую может получить предприниматель, инвестировав имеющийся капитал, равна 8275, при объеме производства равном 50 единицам в проекте A и 110 единицам в проекте B. Таким образом, можно вычислить наиболее выгодное распределение инвестиционного капитала в проектах A и B:
А: 10*50-0,1*502=500-250=250, B: 12*110-0,1*1102=110.
То есть, более прибыльным вариантом распределения капитала будет вложение 250 единиц в проект A и 110 единиц в проект B.
Библиографическая ссылка
Рыбачева Е.А., Севастьянова С.А. ОПТИМИЗАЦИЯ РАСПРЕДЕЛЕНИЯ ИНВЕСТИЦИОННОГО КАПИТАЛА // Современные наукоемкие технологии. 2014. № 7-3. С. 42-43;URL: https://top-technologies.ru/ru/article/view?id=34503 (дата обращения: 25.01.2026).



