Неразрывная связь между экономикой и математикой очевидна. Чем глубже исследования в области математики, тем более точные данные возможно получить в экономической сфере.
Применение определенного интеграла в экономике давно перестало считаться нововведением. Но, если говорить о необходимых расчетах в условиях работы различных компаний, предприятий, можно рассматривать все расчеты с точки зрения программирования. Поэтому применение интегральных уравнений для решения экономических задач будет рассматриваться в качестве необходимого материала для учащихся средних и высших учебных учреждений.
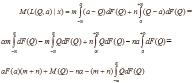
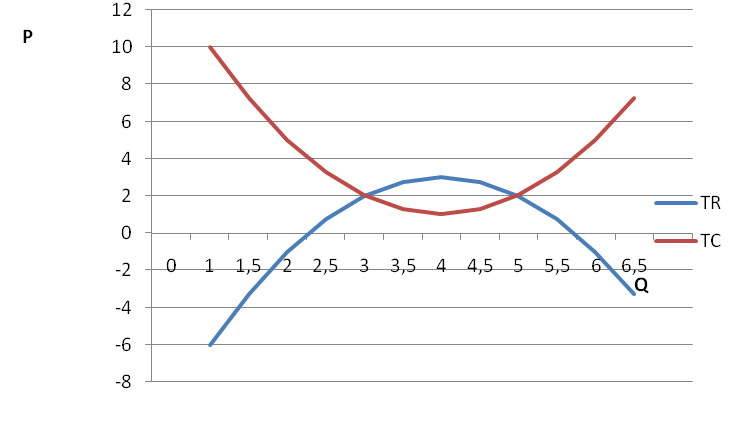
Рисунок 1
Остановимся на вычислении суммарной экономической прибыли фирмы в долгосрочном периоде. Обозначим:P(price)-цена данного товара, выпускаемого фирмой;Q(quantity)-объем товара, выпускаемый производителем;TR(total revenue)-валовой доход, TC(total costs)-валовые издержки.
Движущей силой деятельности фирмы является прибыль. Обозначим ее P(profit).Тогда P=TR-TC. Пусть TR=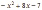 ; TC=
; TC=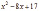 .
.
Графики функций TR и TC представляют собой параболы, ветви которых соответственно направлены вниз и вверх (см. рисунок 1 ) Абсциссы точек пересечения графиков равны 2 и 5.
Координаты точек пересечения графиков функций TR и TC соответственно отображают объем выпускаемой продукции, при котором фирма-производитель будет иметь только нормальную прибыль, при которой TR-TC=0. Нас интересуют расчеты экономической прибыли в длительном периоде, т.к. предприятие в течение времени t увеличивает объем выпуска.
При помощи интегрального уравнения достаточно легко получить искомое значение. Пределами интегрирования являются значения Q1 и Q2, при которых TR=TC. Следовательно, зона экономической прибыли равна разности интегралов
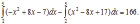
Имея данные фирмы об объемах производства, производственных мощностях расходах и доходах, становится возможным вычисление прибыли за конкретный период.
Расчет экономической прибыли возможен при анализе иных функций: как при сравнении объема максимизирующей прибыли, возможно сравнение как TC и TR в длительном периоде, так и MR и TR в короткосрочном.
Библиографическая ссылка
Паничева А.В. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ ПРИ РАСЧЕТЕ ЭКОНОМИЧЕСКОЙ ПРИБЫЛИ // Современные наукоемкие технологии. 2014. № 7-3. С. 40-41;URL: https://top-technologies.ru/ru/article/view?id=34501 (дата обращения: 14.12.2025).



