Базовой задачей экономического анализа является изучение экономических величин, записываемых в виде функций. Например, увеличение дохода государства при увеличении налогов или при введении импортных пошлин, увеличение или уменьшение доходов фирм при повышении цены на ее продукцию. Для решения подобных задач должны быть составлены функции связи входящих в них переменных, которые затем изучаются с помощью методов дифференциального исчисления функции одной и той же переменной.
В экономике очень часто требуется найти наибольшее или наименьшее значение того или иного показателя: наивысшую производительность труда, максимальную прибыль, максимальный выпуск, минимальные издержки и т.д. Каждый показатель представляет собой функцию нескольких аргументов. Выпуск можно рассматривать как функцию затрат труда и капитала, который обычно зависит от многих факторов и нахождения оптимального значения показателя сводится к нахождению экстремума (максимума или минимума) функции нескольких переменных.
Рассмотрим применение функций нескольких переменных на примере использования ресурсов.
Требуется найти значения величин используемых ресурсов (х, у), при которых фирма – производитель получит наибольшую прибыль, если известна зависимость выпуска продукции от затрат ресурсов (х, у), которая называется производственной функцией.
Производственная функция в денежном выражении равна доходу от использованных ресурсов
(p1,p2) – вектор цен на единицу ресурсов, где p1=2, p2=1/4.
Q(х) = p1x+p2y –затраты на ресурсы, тогда функция прибыли равна
Z(x,y)=20![]() -p1x-p2y
-p1x-p2y![]() Z(x,y)=20
Z(x,y)=20![]()
Для нахождения наибольшей прибыли исследуем функцию Z(x,y) на экстремум. Определим стационарные точки функции из уравнения:
Zх’ =20 * 1/2-1/2![]() =10x-1/2y1/4=p1
=10x-1/2y1/4=p1
Zy’ =20 *1/41/2-3/4=5x1/2y-3/4=p2
Так какZх’=0; Zy’=0
По необходимому условию существования экстремума:
![]()
![]() или
или 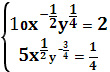
Решением системы уравнений являются числа x=1250, y=5000.
Критическая точка имеет координаты М(1250;5000).
Применим достаточное условие существование экстремума для функции 2-х переменных.
Применим достаточное условие существования экстремума для функции двух переменных
Найдем:
![]() ;
;
![]() ;
;
![]() .
.
Вычислим:
![]()
Следовательно, точка М(1250;5000) – точка экстремума и точка максимума, т.к. ![]()
Библиографическая ссылка
Воропаева А.С., Сидорова А.В., Уфимцева Л.И. ОПТИМИЗАЦИЯ ВЫПУСКА ПРОДУКЦИИ НА ОСНОВЕ ПРОИЗВОДСТВЕННОЙ ФУНКЦИИ // Современные наукоемкие технологии. 2014. № 7-3. С. 36-36;URL: https://top-technologies.ru/ru/article/view?id=34496 (дата обращения: 25.01.2026).



