Технологические операции (перегрузка, дробление, грохочение и др. сыпучих материалов) на предприятиях различных отраслей (горно-рудной, строительной, металлургической, угольной и др.) сопровождаются интенсивным выделением пыли [4, 9].
Наиболее эффективным методом борьбы с пылью является система комплексной обеспыливающей вентиляции включающих в себя: аспирацию, вакуумную систему пылеуборки и общеобменную вентиляцию[4-7].
Системы аспирации ликвидирует основную причину пылеобразования – избыточное давление в полостях технологического оборудования и укрытиях, образующееся при взаимодействии сыпучего материала и рабочих органов с воздухом. Аспирационные установки состоят из укрытия источника пылеобразования, пылеуловителя, вентилятора и сети воздуховодов.
На сегодняшний день существует порядка шестидесяти различных видов аспирационных укрытий, большинство из них имеет достаточно сложные конструкции, значительно снижающие эксплуатационную эффективность работы перегрузочного узла. Наибольшее распространение сегодня получили укрытия с одинарными (УО) и двойными (УД) стенками, а также комбинация двойных стенок с жесткой перегородкой (УДЖ).
Сотрудниками кафедры ТГВ была предложена оригинальная конструкция укрытия (рис. 1) работающего с эффектом двойных стенок и имеющего меньшие габариты по сравнению с аналогами [2, 3, 8]. Для определения конструктивно-технологических параметров данного типа укрытия необходимо произвести ряд исследований по выявлению степени их влияния на объемы эжектируемого воздуха.
Исследования Бутакова С.Е., НединаВ.В., НейковаО.Д., Минко В.А., ЛогачеваИ.Н., Афанасьева И.И., Данченко Ф.И., Пирогова Ю.И., Овсянникова Ю.Г. показали, что в значительной степени на объемы воздуха поступающего по желобу оказывает влияние коэффициент местного сопротивления тракта «верхнее укрытие – желоб – нижнее укрытие» [4-7].
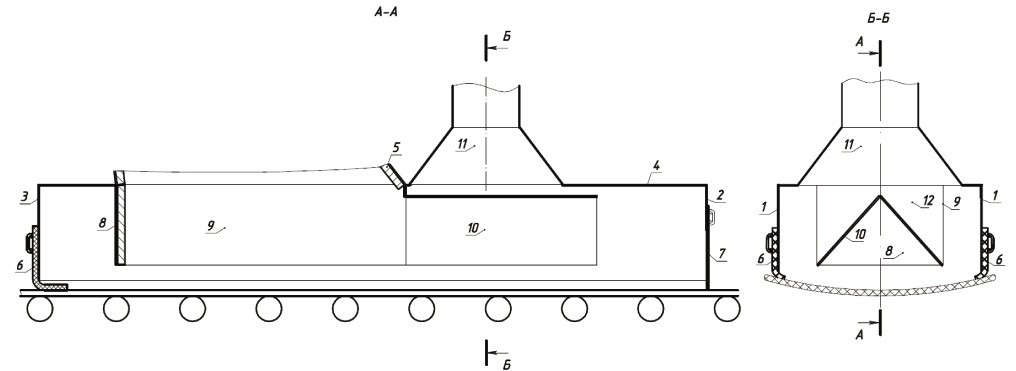
Рис. 1. Аспирационное укрытие мест перегрузки сыпучих материалов [2]: 1 – верхняя крышка; 2, 3, 4 – задняя, передняя и боковые стенки; 5 – перегрузочный желоб; 6, 7 - эластичные уплотнения; 8 – задняя стенка внутреннего короба; 9 – боковые стенки внутреннего короба; 10 – боковые наклонные стенки внутреннего короба; 11 – аспирационная воронка; 12 – передняя стенка внутреннего короба.
Коэффициент аэродинамического сопротивления предлагаемой конструкции укрытия не известен и его приближенное определение возможно только по [1].Необходимо произвести исследования с целью разработки математической модели по определению местного сопротивления разработанной конструкции укрытия [3, 8].
Анализируя конструкцию укрытия, можно предположить, что потери давления в укрытии будут осуществляться при повороте потока, изменении площади поперечного сечения и за счет трения о стенки укрытия.
Для получения математической зависимости, позволяющей провести количественную оценку величины гидравлического сопротивления разработанного аспирационного укрытия, был реализован двух факторный эксперимент. В качестве функции отклика определялась величина КМС аспирационного укрытия xау, рассчитываемая как перепад полных давлений до и после внутреннего короба укрытия, отнесенный к динамическому давлению эжекционного потока. Факторами, обуславливающими значение xау, являлись: угол поворота тракта «желоб-укрытие» (угол наклона желоба к конвейерной ленте) и степень сужения n=F1/F0.
Эксперимент проводился на лабораторном стенде (рис. 2, 3). Работа экспериментальной установки происходит следующим образом: вентилятор 1 подает воздух через воздуховод 2 в канал 3 имитирующий перегрузочный желоб (300х300 мм), после чего воздух попадает в аспирационное укрытие 4.
Изменение расхода эжектируемого воздуха Qж происходит за счет повышения или понижения частоты вращения вентилятора 1.
Определение объемов эжектируемого воздуха производилось при помощи термоанемометра TESTO 425, перепад давления измерялся дифференциальным манометромTESTO 510 с пневмометрической трубкой НИИОГАЗ.
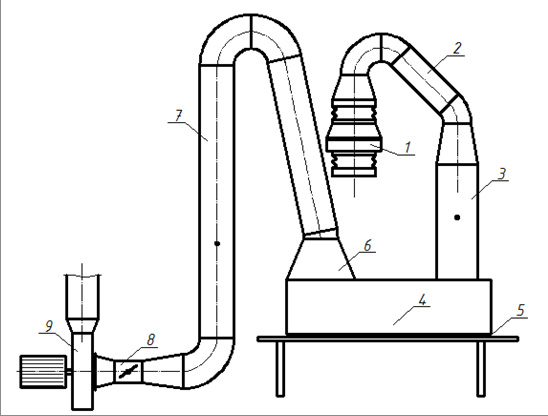
Рис 2. Эксперементальный стенд по исследованию аэродинамических характеристик аспирационных укыртий: 1, 9 – вентиляторы, 2, 3, 7 – воздуховоды; 4 – укрытие; 5 – неплотности в укрытии; 6 – аспирационная воронка; 8 – заслонка.
Обработка результатов эксперимента позволила получить уравнение регрессии в виде квадратичной функции:
Y=bo+∑bi · Xi+ ∑ bij · Xi · Xj + ∑ bii · Xi2
где Y - функция отклика; bo - свободный член уравнения; bi, bij, bii - коэффициенты, соответственно, при линейных параметрах, при эффектах взаимодействия и квадратичных членах; Xi, Xj– уровни варьирования факторов.
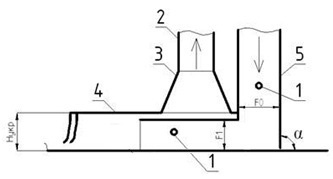
Рис. 3. Схема укрытия экспериментальной установки:1 – точки замера, 2 – воздуховод, 3 – аспирационная воронка, 4 – укрытие, 5 – желоб.
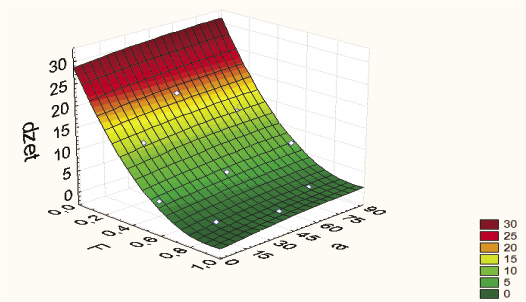
Рис4. Поверхность отклика функциональной зависимости
После проведения расчета коэффициентов уравнения регрессии и оценки их значимости выполненной в программе Statistica 6.0 было получено следующие выражение для определения КМС аспирационного укрытия:
ζау=28,83 -64,35·n+0,0422·a +34,69·n2 - 0,0002·a2,
Зависимость будет справедлива при α=150…900, n=0,2…1 и Re=104…2∙105.
где n=F1/F0 (отношения площади поперечного сечения внутреннего короба укрытия к площади желоба), α-угол наклона желоба к конвейерной ленте.
На основании полученного уравнения регресии был построен график функции отклика (рис4). Указанные значения свидетельствуют о существенном воздействии на коэффициент местного сопротивления соотношения площадей поперечного сечения внутреннего короба укрытия к площади желоба.
В результате проведения эксперимента были выявлены зависимости для определения КМС разработанного укрытия, использование которых позволит вести расчет объемов эжектируемого воздуха с учетом конструктивных особенностей предложенного укрытия.
Библиографическая ссылка
Кологривых А.С., Шумский А.С., Гольцов А.Б. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА МЕСТНОГО СОПРОТИВЛЕНИЯ АСПИРАЦИОННОГО УКРЫТИЯ // Современные наукоемкие технологии. 2014. № 7-2. С. 63-64;URL: https://top-technologies.ru/ru/article/view?id=34308 (дата обращения: 14.03.2026).



