От правильно выбранного лечения пациентов зависит не только их здоровье, но и жизнь, поэтому формализация и оценка методов лечения является очень важной задачей. Использование математических моделей может усовершенствовать выбор наиболее эффективного лечения с учетом затрат.
Для решения задачи поиска наиболее эффективной методики лечения бронхиальной астмы использован рекуррентный метод, реализующий дискретный Марковский процесс. Применение данного метода целесообразно в тех случаях, когда болезнь можно разделить на ряд последовательных фаз (стадий или степеней). Выбранная модель допускает, что пациент находится всегда в одном состоянии здоровья (из конечного количества состояний), которые называют состояниями Маркова; с течением времени возможен переход из одного состояния в другое с известной вероятностью и значением показателя «затраты – эффективность».
В основе выбора оптимальной методики лечения лежит метод «затраты – эффективность» клинико-экономического анализа, принципами которого являются: сравнимость, комплексность, всеобъемлемость, воспроизводимость и точность [1].
В решаемой задаче поиска наиболее эффективной методики лечения бронхиальной астмы выделены 3 состояния Маркова (N=3):
- подозрение на бронхиальную астму;
- обострение;
- ремиссия, то есть временное ослабление или исчезновение признаков астмы. Необходимо отметить, что бронхиальную астму невозможно вылечить окончательно; состояние, к которому необходимо стремиться при лечении, – длительная ремиссия, при которой обострения не отмечаются в течение многих лет.
В качестве стратегий могут быть выделены формы лечения:
- амбулаторное лечение,
- в дневном стационаре,
- в круглосуточном стационаре.
Также в качестве стратегий могут быть рассмотрены методы лечения, то есть некоторые совокупности медицинских вмешательств. Использование препаратов при лечении бронхиальной астмы зависит от состояния больного: одни препараты используются как базисная терапия для предупреждения обострения, другие для облегчения симптомов, третьи при тяжелых обострениях.
Затраты на каждую стратегию k при переходе из состояния i в состояние j (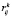
) оценены с помощью модели стохастического программирования, целью которой является нахождение оптимальных по стоимости и эффективности совокупностей медицинских вмешательств. Отметим, что 
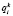– ожидаемые затраты при переходе из состояния i и выборе стратегии k, vi(n) – полные ожидаемые затраты при выборе i стратегии на шаге n.
Вероятности перехода пациента из состояния i в состояние j с помощью стратегии k (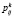
) найдем на основании статистики методов лечения. В состояние «подозрение на бронхиальную астму» невозможно перейти из стадий ремиссии и обострения, поэтому вероятность перехода в данных случаях равны 0.
За шаг моделирование принят 1 месяц, общее количество шагов равно n. При прохождении выбранного количества шагов моделирования находится решение di(n), равное значению оптимальных по стоимости и эффективности совокупностей медицинских вмешательств для каждого из N состояний.
При решении поставленной задачи необходимо следовать алгоритму [3]:
Шаг 1. Вычисление ожидаемых затрат за один переход при выходе из i-го состояния и при выборе стратегии k:
,
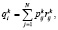
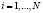где i, j – состояния пациента.
Шаг 2. Нахождение полных ожидаемых затрат за n шагов при оптимальном поведении, если система отправляется из состояния i:
.
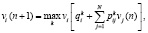
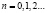Шаг 3. Нахождение решения
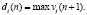
При заданных граничных затратах процесса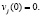 
Таким образом, в ходе решения задачи поиска наиболее эффективной методики лечения бронхиальной астмы выбирается оптимальная по критерию «затраты – эффективность» совокупность медицинских процедур для пациента, находящегося в одном из трех состояний заболевания. В докладе представлены предварительно найденные вероятности и математические ожидания затрат при различных формах и методиках лечения детей, дан сравнительный анализ и решение, полученное с помощью рассмотренного метода.
Библиографическая ссылка
Асмаева А.А., Николаева М.А., Нургалеева Р.Ш. МАРКОВСКИЕ ПРОЦЕССЫ С ДОХОДНОСТЬЮ В ЗАДАЧЕ ВЫБОРА ЭФФЕКТИВНОЙ МЕТОДИКИ ЛЕЧЕНИЯ // Современные наукоемкие технологии. – 2014. – № 7-1. – С. 181-182;URL: https://top-technologies.ru/ru/article/view?id=34274 (дата обращения: 19.04.2024).