Введение
При описании свойств произвольных деформируемых сплошных среды считается заданным либо поле 4-скоростей ( точка зрения Эйлера ), либо закон движения сплошной среды, устанавливающий связь между переменными Эйлера и Лагранжа. Пространство – время считается либо плоским – в случае специальной теории относительности (СТО), либо римановым – в случае общей теории относительности (ОТО). В СТО поля не искривляют пространства – времени, оставляя ее пространственно – временную геометрию плоской. Искривляются, быть может, только “ пространственные сечения. “ Такая точка зрения является наиболее распространенной в теории относительности (ТО). Мы хотим доказать ошибочность такого подхода, связанного с существующим переходом от ИСО к НСО.
1. О трудностях задания лагранжевых сопутствующих среде НСО в СТО
В задаче Дж. Белла [1] показано, что струна, соединяющая одинаковые точечные ракеты, движущиеся равноускоренно с одинаковыми постоянными ускорениями в системе в системе космонавтов разрывается, хотя ее длина в инерциальной системе осчета (ИСО) не меняется. Решение [1] использовано и для расчета движения электронного сгустка в линейных коллайдерах в постоянном электрическом поле [2]. Одной из трудностей является неопределенность в задании пространственной “физической” длины. Например, в НСО, сопутствующей сгустку, или струне в задаче Белла не существует правильной формулы для мгновенной длины. Пусть сигнатура пространства Минковского (+ – - -), греческие индексы изменяются от 0 до 3, а латинские от 1 до 3. Формула для вычисления элемента квадрата физического расстояния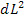 
c помощью пространственного метрического тензора [6]
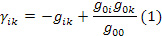
используется неправильно. Правильное (в рамках СТО) использование этой формулы на гиперповерхности ортогональной мировым линиям частиц сгустка, что и является мгновенным физическим пространством, сопутствующим среде наблюдателям, привела к соотношению [3-5]
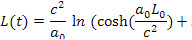
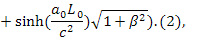
где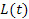 
– длина сгустка (или нити в задаче Белла) в сопутствующей сгусту системе отсчета, как функция времени ИСО 
, 
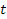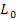– начальная длина сгустка (нити), 
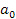– постоянное ускорение, 
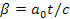. Последняя формула оригинальна и в научной литературе до работ [3-5] не встречалась. Стандартный расчет по формуле (1) из [6] в [2], [7]
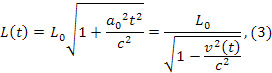
в котором пренебрегается кривизной пространственно подобной кривой, ортогональной мировым линиям частиц среды, дает в конце разгона в лагранжевой сопутствующей НСО увеличение длины сгустка в электронном коллайдере [2] до 10000 раз. Подход [8], основанный на вычислениии расстояния вдоль орта некоторой мгновенно сопутствующей системы отсчета ((МСИСО) от начала сгустка к концу приводит к практическому обнулению длины сгустка в конце разгона. В [3-5] при тех же условиях длина сгустка возрастает в 1.003 раза.
В задаче Белла, при условии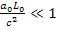 
все формулы из перечисленных работ совпадают. И все авторы приходят к выводу о разрыве нити в задаче Белла. Однако разрыв струны все перечисленные авторы (кроме [3-5]) связывают с лоренцевыми сокращениями. На наш взгляд это вообще неправильно. Согласно Паули и Герглотцу, которые заложили основы релятивистской теории упругости, именно уклонение от жесткости по Борну, а не лоренцевы сокращения приводят к деформациям и напряжениям в теле. Для определения истинных деформаций в теле (стержне) нужно следить именно за этим телом, а не сравнивать его длину с другим аналогичным стержнем в некоторой МСИСО. Ситуация напоминает сравнение длины столба с его тенью от солнца. Связывать преобразование Лоренца с переходом от одной ИСО к другой – грубая ошибка. Лоренцевы преобразования это правило пересчета геометрических объектов (полей) от одной ИСО к другой, которые никогда по определению не совпадали. Пусть для примера в одной ИСО находится хрупкий очень тонкий стеклянный стержень, который разлетается на куски при малейших деформациях. Пусть имеется набор с аналогичными стержнями в других ИСО, движущихся с релятивистскими скоростями. Для каждого из наблюдателей на стержне его стержень не ломается, а стержни других в согласии с лоренцевыми сокращениями должны разлететься на куски. Ситуация абсурдна, так как целостность или разрывы на куски для стержней есть инвариантный фактор. Это напоминает стендовую стрельбу по тарелочкам, когда один стрелок тарелочку разбивает вдребезги. А для наблюдателя из другой ИСО, кажется, что тарелочка остается целой и стрелок промахнулся. Трактовка преобразований Лоренца, как переход от одной ИСО к другой, аналогична действию пассажира вскочить с платформы в быстро мчащийся мимо экспресс.
При построении релятивистской теории упругости переходят в лагранжеву сопутствующую НСО, где лоренцевых сокращений нет по определению. Возникновение деформаций и напряжений в среде происходит в том случае, когда среда движется не как жесткое в смысле Борна тело. Уклонение от жесткости по Борну приводит к отличному от нуля тензору скоростей деформаций. С нашей точки зрения нить разорвется, если строго придерживаться подхода СТО, на основе общепринятых правил перехода от ИСО к НСО, но не за счет лоренцевых сокращений, как это утверждается в перечисленных работах, а за счет того, при таком движении нарушается релятивистская жесткость струны (по Борну) и в струне возникают деформации и напряжения.
2. Связь геометрии
пространства-времени с параметрами сплошной среды и с силовыми полями, решение задачи Белла
В ньютоновской механике и СТО материальная точка имеют нулевое абсолютное ускорение относительно ИСО, когда отсутствуют приложеннные к ней силы или их векторная сумма равна нулю. В ОТО этот правило не выполняется. Покоящееся на поверхности гравитирующего шара материальная точка, в согласии с ОТО имеет отличный от нуля вектор первой кривизны (4 – ускорение). Абсолютное ускорение направленно по внешней нормали к сфере и равно по величине ньютоновскому ускорению свободного падения вблизи поверхности. Сила реакции опоры со стороны поверхности сферы сбивает тело с его геодезической линии, имеющей нулевой вектор первой кривизны только при отсутствии реакции опоры. По Ньютону абсолютное ускорение материальной точки на поверхности сферы равно нулю. Для слабых полей уравнения Эйнштейна совпадают с теорией Ньютона, однако принцип соответствия по отношению к абсолютным ускорениям не применим.
О характере силового поля можно судить по движению или покою пробных частиц в этом поле. По определению пробные частицы друг с другом не взаимодействуют, а взаимодействуют только с внешним полем. Пусть пробные частицы одинаковы и представляют некоторую сплошную среду. Характеристиками сплошной среды в 4-пространстве – времени, являются 4-ускорение, тензор скоростей деформаций, и тензор угловой скорости вращения. 4 -ускорение входит в закон движения и при заданной плоской метрике интегрированием уравнения движения определяется поле 4 – скорости и основные тензоры среды. Сплошная среда в силовом поле задает некую систему отсчета (СО) Для СО с заданными из физических требований свойствами необходимо знать дополнительные условия, приписываемые основным тензорам среды, зависящим от 4 – скоростей и 4 – ускорений. Например, требовние о вращении и жесткости по Борну. Число уравнений для нахождения 4- скорости становится переопределенным и должны выполняться условия интегрируемости. Последние выполнятся, если искомыми будут не только 4 – скорости среды, но и метрические коэффициенты. Для существования решения нами получены условия интегрируемости (уравнения структуры) [11], [9], [16], [17] . В работах [3], [4], [5], [10], [15] подробно разобраны примеры их применения. Уравнения структуры, являясь точными, не связаны непосредственно с уравнениями Эйнштейна.
Для движущейся (или покоящейся) сплошной среды имеют место соотношения.
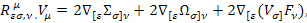
для которых в движущейся сплошной среды в четырехмерном пространстве – времени справедливы выражения
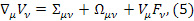
где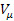 
– поле 4 – скорости , удовлетворяющее условию нормировки
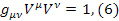
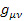– метрический тензор в системе отсчета Эйлера ,
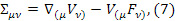
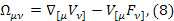
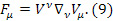
где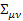 
– тензор скоростей деформаций, 
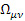– тензор угловой скорости вращения 
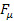– векторы первой кривизны мировых линий частиц среды.
Интегрирование системы (4-9), где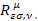 
– тензор кривизны, выражаемый через метрический тензор обычным образом , дает решение задачи о геометрии пространства – времени, в которой реализуется НСО с заданной структурой. В [9,10] доказана теорема, что жесткая по Борну равноускоренная среда может быть описана в рамках пространства Римана. Хотя уравнения структуры не связаны с ОТО, но накладывают дополнительные условия к уравнениям Эйнштейна. Доказана теорема, что все статические сферически-симметричные решения ОТО совместны с уравнением структуры. Одномерного решения вне плоского бесконечного массивного источника в ОТО не существует, а уравнение структуры имеет его и индуцирует метрику для постоянного однородного статического поля [10]. Расчет, проведенный в лагранжевой сопутствующей НСО приводит к метрике
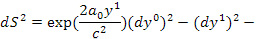
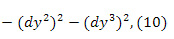
где ускорение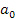 
считается положительным, если направлено вдоль оси 
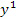и отрицательным, если против этой оси. Метрика (10) впервые получена в работе [11] и повторена в [12], [13]. Одна независимая компонента тензора кривизны, вычисленная по метрике (10), имеет вид
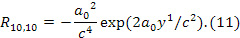
Для компонент тензора Риччи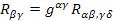 
и скалярной кривизны 
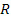имеем
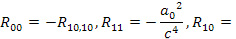
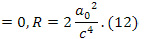
В равноускоренности НСО (12) можно убедиться непосредственно
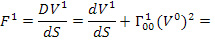
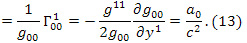
Остальные компоненты 4-ускорения равны нулю.
Метрику (10) можно трактовать и как равновесие пробных частиц в постоянном однородном силовом поле любой природы. Пусть на невесомых нитях в однородном постоянном электрическом поле подвешены одинаковые пробные заряды с одинаковой массой. Из физических соображений ясно, что заряды покоятся друг относительно друга (модель заряженной пыли) и натяжения всех нитей одинаковы.
Допустимы две точки зрения:
1. Пространство-время плоское и сумма сил на каждый из зарядов равна нулю. 2. Пространство- время риманово с плоским сечением и вектор 4-ускорения постоянен и вычисляется по (13).
Исследование электростатики в пространстве Римана подробно рассмотрено в [10], а система решений уравнений Эйнштейна-Максвелла, совместная с уравнениями структуры, найдена в [14,15].
Остановимся на решении задачи Белла. Будем развивать вторую точку зрения. В римановой геометрии, закрепленная в поле частица, имеет вектор первой кривизны (4- ускорение) отличный от нуля, а в пространстве Минковского эта же частица имеет прямую мировую линию с 4-ускорением равным нулю. Из принципа глобальной эквивалентности, закрепление частиц в однородном постоянном силовом поле эквивалентно их нахождению в жесткой по Борну релятивистски глобально равноускоренной НСО. В задаче Белла при старте двух точечных ракет с одинаковыми в системе космонавтов постоянными ускорениями после затухания колебаний, закрепленные на невесомой нити и ракетах идеальные невесомые акселерометры, покажут одинаковые величины. Из одинаковых физических условий обе ракеты в системе космонавтов взаимно неподвижны. Следовательно, метрика для нити в системе космонавтов совпадает с (10). И длина нити в НСО сохраняется. Парадокс возник из-за стандартного принятого на данный момент перехода от ИСО к НСО. О сомнениях к такому подходу неоднократно говорил В.И. Родичев [22], идеи которого незаслуженно забыты. А.А. Власов [23], рассматривая теорию роста кристаллических, плазменных и биологических структур с сохранением их подобия, пришел к результату, что рост таких структур возможен в неевклидовом пространстве-времени. Другие возможност переходов подробно изложены в [9, 16, 17, 11]. Хотя формула (2) пригодна и для больших, и для малых ускорений, она принципиально не решает парадокса Белла. Парадокс решается только при выходе из пространства Минковского в пространство Римана. Выведенная формула (2) в рамках СТО верна только в случае стандартного перехода от ИСО к НСО.
Отметим, что пространство – время искривлено в ускоренных точечных ракетах и нити только в пределе мировой полосы.
3. Релятивистская жесткая равномерно вращающаяся НСО
При рассмотрении вращающегося диска обычно выбирают неподвижную систему отсчета, в которой вводят цилиндрические координаты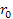 
, 
, 
, 
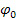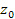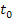и переходят к вращающейся системе отсчета 
, 
, 
, 
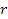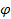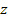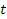согласно формулам:
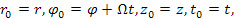
где угловая скорость вращения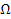 
относительно оси 
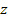считается постоянной. Элемент интервала имеет вид
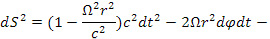
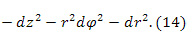
Формула справедлива, если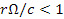 
. В работах [18, 19], обсуждаются другие распределения скоростей, которые ограничивают линейную скорость вращения диска при 
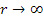величиной скорости света 
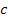, а при 
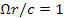дают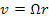 
. Однако критерию жесткости как классическому, так и релятивистскому (в смысле Борна) удовлетворяет только обычный закон распределения 
, 
.
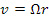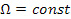Найдем метрику жесткой релятивистской равномерно вращающейся НСО с помощью нашего метода, полагая в формулах тензор скоростей деформаций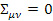 
и требуя постоянства инварианта, характеризующего релятивистское обобщение квадрата угловой скорости вращения диска 
.
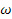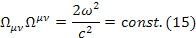
В лагранжевой сопутствующей системе отсчета, связанной с вращающимся диском, имеем
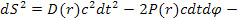
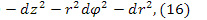
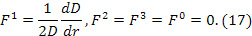
После громоздких вычислений имеем два независимых уравнения
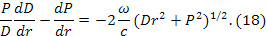
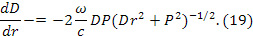
Условие (15) эквивалентно постоянству величины хронометрически инвариантного вектора угловой скорости [20] и постоянству величины угловой скорости в сопутствующих тетрадах [21].
Величины релятивистской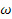 
и классической угловой скорости 
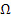связаны соотношением
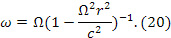
Для метрики (16) существует стационарное решение, применимое для всей области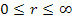 
, но реализуемое в римановом пространстве-времени. Решения системы (18), (19) в квадратурах получить не удалось. Численный анализ показал, что при 
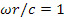метрика (16) совпадает с метрикой (14). Центростремительное ускорение во вращающейся НСО определяется формулой
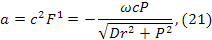
которая при малых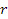 
переходит в классическую, а при 
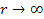дает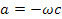 
. Вычисление независимых отличных от нуля компонент тензора кривизны громоздки и их опускаем, отсылая к работам [9], [11], [16], [17]. После упрощений система (18,19) представляется в форме
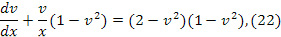
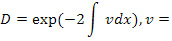
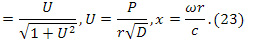
Физический смысл функции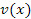 
означает безразмерную линейную скорость диска. Для малых скоростей (фор. 24)
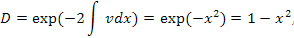
что эквивалентно классическому выражению. Из анализа (22) следует, что для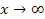 
уравнение имеет решение 
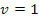. Это решение резко отличается от классического жесткого диска, где поле скоростей на бесконечности неограниченно велико. График численного решения (22) по виду напоминает график гиперболического тангенса или деформированной ступенчатой функции для 
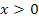. Считается [6] , что на вращающемся диске часы не могут быть однозначно синхронизированы во всех точках. «Поэтому, производя синхронизацию вдоль замкнутого контура и возвращаясь в исходную точку, мы получим время, отличающееся от первоначального на величину [6]»
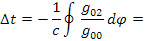
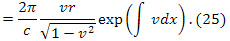
На наш взгляд, такое утверждение ошибочно. В формуле (25) контур в «физическом» пространстве не замкнут. Разобъем вращающийся диск на концентрические окружности и рассмотрим частицы на одной из них. Мировые линии частиц этой окружности в пространстве Минковского ( что справедливо для малых скоростей) образуют образуют конгруенцию винтовых линий на цилиндре радиуса r, а «физическим» пространством будет конгруенция пространственно подобных винтовых линий, ортогональных конгруенции мировых линий частиц окружности. Эта конгруенция находится из уравнения Пфаффа (по анологии с [3,4]) и приводит к формуле (25). Ясно, что точки 0 и 2π не совпадают друг с другом и разделены в пространстве-времени временным интервалом (25), хотя являются одними и теми же лагранжевыми пространственными точками. Временной зазор (25) равен шагу винтовой линии «физического» пространства, не совпадающего с шагом мировых винтовых линий частиц окружности. И ни о каком отсутствии однозначности синхронизации не идет речи. Просто временное расстояние до разных точек «физического» пространства или разных точек винтовой линии различно.
Рассмотрим распространение световых лучей по отношению к источнику в ИСО, расположенному в начале эйлеровых и лагранжевых координат. Световые импульсы испущены одновременно навстречу друг другу по окружности, совпадающей с одной из окружностей вращающегося диска. Скорость света в ИСО постоянна. Но так как диск вращается, то «догоняющий» импульс затрачивает больше времени до встречи с лагранжевой точкой 2π на величину (25). Импульс, распространяющийся навстечу линейной скорости на вращающейся окружности затрачивает меньше времени на эту же величину. По мировому времени разность времен достижения лагранжевой точки 2π равна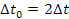 
. В нерелятивистском приближении для малых скоростей диска 
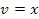найденный результат совпадает с результатом известного опыта Саньяка.
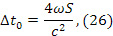
где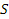 
– площадь диска. В ультрарелятивистском случае имеем
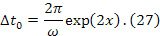
В заключение отметим, что расчет не противоречит СТО. Вспомним известный опыт опыт, когда фонарь включается внутри движущегося равномерно поезда, то свет достигает передней и задней стенок вагона одновременно по времени ИСО поезда, но если фонарь включается в ИСО платформы, то световой импульс достигает задней стенки раньше, чем передней. Путаница, связанная с опытом Саньяка, связана с непониманием понятия физического пространства, как гиперповерхности ортогональной мировым линиям частиц среды и неумением вычислять в них мгновенные расстояния (3), о чем подробно объяснено в [3,4].
Заключение
1. В пространстве Минковского невозможно поступательное глобально равноускоренное и жесткое по Борну движение сплошной среды. Если накладывать дополнительные условия на жесткость или вращения сплошной среды, то эти условия “выводят” движущуюся среду из плоского пространства – времени.
2. Приведена метрика жесткой по Борну глобально равноускоренной сплошной среды, реализуемая в римановом пространстве-времени. Метрика объединяет свойства метрики Меллера (жесткость по Борну) и свойства метрики Логунова (глобальная равноускоренность). Собственное время, которое получал Эйнштейн [24] , и которое называл точным, получается из метрики (10) для фиксированной лагранжевой частицы.
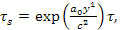
где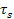 
– собственное время для данной точки пространства, 
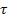– мировое время. Но Эйнштейн по неизвестным причинам отказался от точного выражения в пользу приближенного ( по Меллеру ).
3. Найдена релятивистская жесткая по Борну равномерно вращаюшаяся НСО без ограничения на величину радиуса и имеющая на бесконечности линейную скорость равную скорости света и конечное ускорение, но реализуемая в римановом пространстве времени.
4. Точные уравнения структуры ограничивают область применимости уравнений Эйнштейна, так как дают дополнительные условия, которые не всегда совместимы с решениями ОТО.
5. Решен парадокс Белла.
6. Наделение систем отсчета физическими свойствами эквивалентно введению квантовомеханического принципа дополнительности в ньютоновскую теорию гравитации. Точно так же, как и в квантовой механике атомные системы нельзя описывать независимо от средств наблюдений.
Библиографическая ссылка
Подосенов С.А. УРАВНЕНИЯ СТРУКТУРЫ В РЕЛЯТИВСТСКОЙ МЕХАНИКЕ СПЛОШНЫХ СРЕД И РЕШЕНИЕ ПАРАДОКСА БЕЛЛА // Современные наукоемкие технологии. 2014. № 3. С. 132-138;URL: https://top-technologies.ru/ru/article/view?id=34127 (дата обращения: 03.04.2025).