Введение
В современном обществе защита информации представляет собой комплекс мероприятий, направленных на предотвращение несанкционированной утечки, модификации и удаления информации, осуществляемых с применением технических, в том числе и программных, средств. Основной из основных задач обеспечения безопасности информационных компьютерных систем является защита информации от несанкционированного доступа (НСД) и ограничение круга лиц, имеющих доступ к этой критичной информации. Поэтому разработка математической модели системы защиты информации позволяющей зашифровывать поток данных в реальном масштабе времени является актуальной.
Основная часть
Развитие вычислительной техники, появление новых информационных технологий, обеспечивающих обработку и передачу больших объемов данных, требуют от современных систем защиты информации от НСД высокой производительности. В настоящее время этому требованию отвечают системы поточного шифрования [1,2]. Считается, что шифр, основанный на сложении потока псевдослучайных битов, полученных с помощью линейного регистра сдвига с обратной связью, с битами исходного текста по модулю два, в общем случае теоретически нераспознаваем. Однако такая система шифрования не отличается стойкостью и может быть мгновенно раскрыта при наличии определенного количества символов исходного и шифрованного текста. Уязвимость системы к атакам на основе исходных и подобранных текстов обусловлено тем, что при битовом шифровании потока данных сложение символов по модулю два является единственным способом построения обратимой функции шифрования [2].
В настоящее время одним из перспективных направлений шифрования потока данных является использование математического аппарата расширенных полей Галуа GF(pv). Системы шифрования, использующие поля Галуа GF(pv), обладают более широкими возможностями по реализации различных криптографических функций обеспечения конфиденциальности и целостности информации. Применение в таких системах основных аддитивных и мультипликативных операций, к которым можно отнести сложение по модулю, умножение по модулю, возведение в степень по модулю, и их различных комбинаций позволит повысить уровень защиты информации [3-9]. Наиболее трудоемкой операцией, реализуемой в конечных полях Галуа, является операция возведения в степень по модулю. Это, конечно, приводит к увеличению времени шифрования и дешифрования, но позволяет обеспечить требуемый уровень криптографической защиты от НСД.
Рассмотрим процедуру шифрования потока данных с операцией возведения в степень символов поля Галуа GF(pv). В данной системе выбирается неприводимый полином 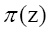
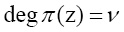 , порождающий все элементы мультипликативной группы данного поля. Входная последовательность разбивается на блоки по
, порождающий все элементы мультипликативной группы данного поля. Входная последовательность разбивается на блоки по 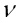 символов в каждом. Такой блок в полиномиальной форме имеет вид
символов в каждом. Такой блок в полиномиальной форме имеет вид
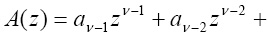
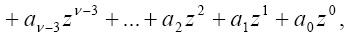 (1)
(1)
где 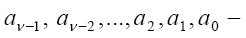 двоичный код блока,
двоичный код блока, 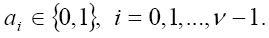
Этот блок считается элементом расширенного поля Галуа GF(pv). Для реализации процедуры шифрования на основе возведения в степень вычисляются значения псевдослучайной последовательности (ПСП) Х, значения которой снимаются с разных 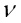 выходов линий задержки генератора. Тогда псевдослучайная последовательность можно представить в виде последовательности
выходов линий задержки генератора. Тогда псевдослучайная последовательность можно представить в виде последовательности
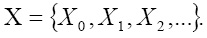 (2)
(2)
В этом случае процедура зашифрования определяется равенством
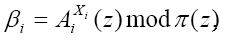 (3)
(3)
где 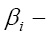 i-й блок зашифрованного сообщения; I = 0, 1, ….
i-й блок зашифрованного сообщения; I = 0, 1, ….
Повысить скорость шифрования можно за счет перехода и индексному представлению элементов полей Галуа, что позволяет свести низкоскоростную операцию возведения в степень по модулю к аддитивной операции [1-4]. В этом случае блок исходных данных в двоичном коде подается на входы устройства вычисления индекса, реализующего
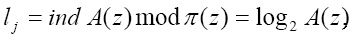 (4)
(4)
где l – индекс блока A(z); α – порождающий элемент мультипликативной группы поля Галуа GF(pv).
Вычисленный lj индекс в виде параллельного кода подается на первые входы умножителя по модулю рν-1. На вторые входы этого умножителя поступает параллельный двоичный код ключа xj ,снятого с выходов генератора ПСП. Умножитель по модулю рν-1 реализует модульную операцию
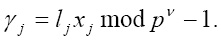 (5)
(5)
Полученный результат γj представляет индекс элемента поля GF(pv), который является результатом зашифрованного блока Аj согласно выражения (3). Он в параллельном виде подается на вход преобразователя «индекс – элемент поля»
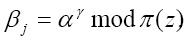 (6)
(6)
В результате зашифрованный блок данных βj, передается на приемную сторону.
Для дешифрования сообщения на приемной стороне решается обратная задача выражению (3). В этом случае j-й блок открытого сообщения j = 0, 1, 2… вычисляется согласно
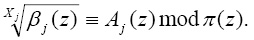 (7)
(7)
Применение полиномиальной системы классов вычетов (ПСКВ) позволяет повысить степень защиты информации от НСД, а также скорость закрытия информации [5]. Если взять для выработки генератор ПСП, в котором число линий задержек значительно превосходит степень 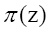 , то есть
, то есть 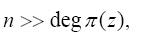 то число символов, которые можно использовать как показатели степени равно
то число символов, которые можно использовать как показатели степени равно
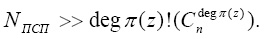 (8)
(8)
Так уже при n = 255 и седьмой степени полинома число возможных ПСП, снимаемых параллельно с выходов различных линий задержки, превысит число 1018, что свидетельствует о высокой степени криптографической защиты.
Кроме того, применение полиномиальной системы классов вычетов позволяет обеспечить защиту информации от возникающих ошибок в процессе передачи и обработки данных. В работах [6-9] представлены различные алгоритмы, позволяющие обнаруживать и корректировать ошибки с использованием избыточных кодов ПСКВ. Для этого необходимо вычислитель соответствующую позиционную характеристику, величина которой позволит однозначно определить местоположение ошибки и ее глубину. Проведенный анализ работ [6-9] показал, что наиболее перспективным методом коррекции ошибок выступает спектральный метод, аппаратная реализация которого приведена в работе [9].
Кроме того, рассматривая вопросы разработки математической модели системы защиты информации от НСД, функционирующей в ПСКВ, нельзя не отметить возможность использования данных кодов для построения схемы разделения секрета [4,10]. Построение такой схемы вызвано необходимости организации безопасной связи внутри групп абонентов с динамически меняющимся составом. Применение ПСКВ позволяет решить данную задачу на основе усовершенствования модулярной пороговой схемы (m, n) разделения секрета. Для этого выбирается полином pl(z), степень которого превышает полиномиальную форму секрета M(z).
Затем выбираются неприводимые полиномы pi(z), удовлетворяющие условию
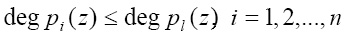 , (9)
, (9)
которые упорядочены по возрастанию степеней
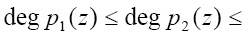
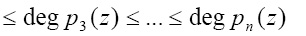 . (10)
. (10)
Для создания (m, n) схемы проверяется выполнение условия
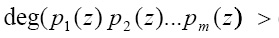
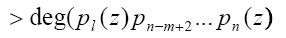 . (11)
. (11)
Чтобы определить доли секрета и их распределить между абонентами группы, выбирается полином r(z) и вычисляется значение
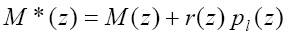 . (12)
. (12)
В качестве долей для каждого пользователя выступают остатки
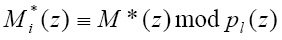 . (13)
. (13)
Используя китайскую теорему об остатках, m пользователей способны восстановить значение M*(z), а затем, зная r(z) и pl(z), определить секрет M(z). При этом группа из m-1 абонентов не способна будет получить значение M(z). Для эффективной работы схемы разделения секрета в ПСКВ необходимо вычислить предельное значение полинома r(z), которое позволило бы при меньших временных затратах вычислить M*(z), и найти значение M(z).
Рассмотрим пороговую схему разделения секрета, функционирующую в полиномиальной системе классов вычетов. Если в (m, n) модулярной полиномиальной пороговой схеме, в которой справедливо
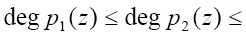
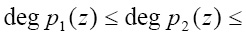 , (14)
, (14)
имеет место условие
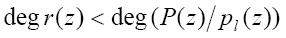 , (15)
, (15)
где 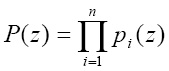 – полный диапазон,
– полный диапазон,
то такая пороговая схема обеспечивает восстановление секрета M(z) для любого набора m пользователей группы, состоящей из n абонентов.
Проведенные исследования показали, что использование полиномиальной системы классов вычетов в схеме разделения секрета позволяет в 2 раза сократить размер вспомогательного полинома r(z) при сохранении уровня защиты от НСД при использовании уже 11 разрядных оснований ПСКВ. При чем при увеличении разрядности оснований ПСКВ данных возрастает выигрыш в системе разделения секрета.
Выводы
В работе показано, что эффективность работы системы защиты информации от НСД во многом зависит от математического аппарата, положенного в основу ее работы. Применение в математической модели ПСКВ в нелинейных системах шифрования позволяет не только повысить скорость шифрования за счет применения индексного представления элементов расширенных полей Галуа, но и осуществлять процедуры поиска и коррекции ошибок, которые возникают в процессе передачи и обработки закрытых данных.
Библиографическая ссылка
Зюзякин Г.И., Калмыков М.И., Петрова Е.В. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ СИСТЕМЫ ЗАЩИТЫ ИНФОРМАЦИИ, ФУНКЦИОНИРУЮЩЕЙ В ПОЛИНОМИАЛЬНОЙ СИСТЕМЕ КЛАССОВ ВЫЧЕТОВ // Современные наукоемкие технологии. 2014. № 3. С. 128-131;URL: https://top-technologies.ru/ru/article/view?id=34126 (дата обращения: 12.03.2026).



