Введение
Существует множество традиционных методов анализа временных рядов. Каждый из них имеет определенные преимущества и недостатки. Одним из основных методов обработки нестационарных временных рядов является спектральный анализ (Фурье-анализ), который позволяет охарактеризовать частотный состав исследуемого сигнала. Недостаток преобразования Фурье заключается в том, что частотные компоненты не могут быть локализованы во времени, что накладывает ограничения на применимость данного метода к ряду задач. Поэтому для решения задачи исследования нестационарных процессов необходимы более современные методы анализа сигналов, изначально предназначенных для нелинейных и нестационарных временных рядов. В работе рассматривается моделирование временных рядов с применением математического аппарата вейвлет и фрактального анализа (ВФА).
Преимущества вейвлет- и фрактального анализа
Вейвлет-базисы могут быть хорошо локализованными, как по частоте, так и по времени. При выделении в сигналах хорошо локализованных разномасштабных процессов можно рассматривать только те масштабные уровни разложения, которые представляют интерес.
Вейвлет-анализ применяется для анализа нестационарных данных и вейвлет-преобразование представляется перспективным математическим аппаратом не только для задач, связанных с анализом сигналов различной природы, но и для решения уравнений, описывающих сложные нелинейные процессы в широких диапазонах масштабов. Он позволяет выявить пространственно-временные свойства изучаемого объекта, определить наличие перемежаемости, получить локальную высокочастотную и глобальную крупномасштабную информацию об объекте достаточно точно и без избыточности и позволяют судить о том, в какой момент времени появились те или иные компоненты сигнала.
Вейвлет-преобразования обладают практически всеми достоинствами преобразований Фурье, но в отличие от него, имеют достаточно много разнообразных базовых функций, свойства которых ориентированы на решение различных задач[2].
Особенность фрактального анализа временных рядов в том, что он учитывает поведение системы не только в период измерений, но и его предысторию. Фрактальная размерность, является показателем сложности кривой. Анализируя чередование участков с различной фрактальной размерностью и тем, как на систему воздействуют внешние и внутренние факторы, можно научиться предсказывать поведение системы, и что самое главное, диагностировать и предсказывать нестабильные состояния.
Целью настоящего исследования является математическое и численное моделирование временных рядов методами вейвлет и фрактального анализа.
Объектом исследования являются временные ряды, предметом исследования – вейвлет и фрактальный анализ. Методологической основой исследования являются: виды численного анализа, фрактальный, вейвлет-, статистический анализ.
Постановка задачи
С помощью предложенных методов вейвлет- и фрактального анализа применительно к временному ряду, представленному числовыми значениями, необходимо получить количественные и качественные оценки, характеризующие нестационарность или хаотичность исследуемого процесса.
Этапы решения задачи
Основной алгоритм обработки строится при условии существования временного ряда, то есть собранного в разные моменты времени статистического материала о значении каких-либо параметров исследуемого процесса, где учитывается взаимосвязь измерений со временем.
Первый этап – это обработка временного ряда методом вейвлет- и фрактального анализа. Комплексное применение этих двух анализов позволит получить более полную информацию об исследуемом процессе, описанного временными рядами.
В работе вейвлет-преобразование осуществляется с помощью прямого WT (Wavelet transformation)[3]:
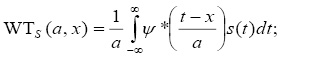
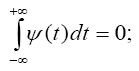
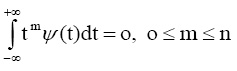
где a – масштабный параметр; х – перенос (сдвиг) материнского вейвлета; s(t) – исходный сигнал; Ψ(t) – вейвлет-функция
Расчет фрактальной размерности в данном исследовании производится поточечным методом. Алгоритм расчета поточечной размерности на сегодняшний момент общеизвестен и является классическим (рис. 1).
Полученные величины фрактальных размерностей исследуемых временных рядов применяются в качестве критерия устойчивости исследуемого процесса. По величине фрактальной размерности можно получить количественную оценку хаотичности исследуемого процесса, а также многофакторность и «насыщенность» предпосылок, вызвавших нестационарности процесса) [1]:
Вторым и заключительным этапом алгоритма модели является построение прогнозной оценки на основе выделения показателей, стремящихся к нестабильному состоянию и предопределяющих неудовлетворительное состояние процесса. Результаты могут быть визуализированы и представлены в виде построенных вейвлет-скалограмм, которые дают наглядную картину наиболее резко меняющихся компонент сигнала. Тем самым появляется возможность выделить наиболее нестационарные области и по выделенным областям более детально провести анализ причин возникновения данных нестационарных событий в сигнале применительно к различным прикладным областям.
Выводы
- Данный алгоритм может быть применен для исследования и прогнозирования, в том числе стохастических социальных процессов, зависящих от большого количества факторов и описанных временными рядами.
- Распределение вейвлет- коэффициентов позволяет выявить нестационарности исследуемого процесса на любых частотно-временных масштабах и тем самым является как качественной, так и количественной характеристикой нестационарности.
- Распределение фрактальных размерностей позволяет получать количественную оценку хаотичности исследуемого процесса
- Данный алгоритм позволяет строить прогнозные оценки с выделением факторов (показателей), предопределяющих неудовлетворительное состояние рассматриваемого процесса
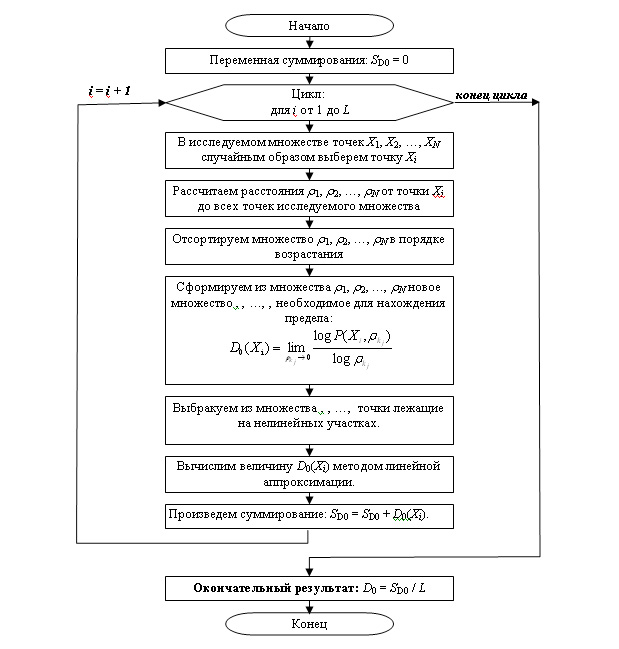
Рис. 1. Блок-схема алгоритма расчета фрактальной размерности Хаусдорфа
Библиографическая ссылка
Амосов О.С., Муллер Н.В. ПРИМЕНЕНИЕ МЕТОДОВ ВЕЙВЛЕТ И ФРАКТАЛЬНОГО АНАЛИЗА ДЛЯ МАТЕМАТИЧЕСКОГО И ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ ВРЕМЕННЫХ РЯДОВ // Современные наукоемкие технологии. 2014. № 3. С. 122-124;URL: https://top-technologies.ru/ru/article/view?id=34124 (дата обращения: 12.03.2026).



