Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Зайкин О.А. 1

---

1 ФГБОУ ВПО «Астраханский государственный технический университет»

В результате анализа тенденций развития современных конструкций приводов транспортно-технологических машин с целью создания нового качественного привода в качестве базового выбран планетарный бесшатунный механизм. При этом учтены следующие его положительные свойства: компактность, уравновешенность, технологичность звеньев, известная апробация в реальном ДВС, повышенный ресурс и КПД, экономичность и экологичность. В настоящей статье приведены результаты экспериментального исследования параметров движения выбранного в качестве базового бесшатунного зубчатого дифференциала, обеспечивающего поступательное движение выходного звена без направляющей. На основе полученных результатов выполнена апробация расчетных зависимостей и выводов, сформулированных на основе расчетных исследований.

Статья в формате PDF

1086 KB

привод

дифференциал

скорость

прямолинейная траектория

тензометрическая станция

датчик

крутящий момент.

1. Патент РФ № 5056238/28, 24.07.1992

2. Патент РФ № 94030365/28, 16.08.1994

3. Патент РФ № 98109210/28, 15.05.1998

4. Патент РФ № 98109187/28, 15.05.1998

Введение

Для приводов транспортно-технологических машин автором разработаны четыре схемы бесшатунных замкнутых дифференциалов зубчатого типа [1, 2, 3, 4] с улучшенными техническими параметрами. Исследования параметров их движения расчетным методом показали, что:

– они могут формировать точную прямолинейную траекторию выходного звена при особой кинематике сателлита и центрального колеса;

– колеса движутся с постоянной угловой скоростью, а точки прямолинейного движения – по графику синусной гармонической функции;

– при нарушении кинематики прямая вырождается в циклическую гипоциклоиду, описывающую окружность за множество цикловых повторений;

– при нарушении радиуса положения точки на сателлите с прямой траекторией прямая преобразуется в устойчивый эллипс с малой осью, равной удвоенному отклонению;

– сопротивление движению механизмов каждой схемы различно, поэтому не все схемы можно приводить в движение через водило;

– КПД при разных входных валах различный, что позволяет найти экономичную конструкцию при свободном выборе ведущего вала.

Эти результаты теоретических исследований свидетельствуют о повышенном качестве новых дифференциальных схем, но требуют практического подтверждения для правильного выбора их параметров при проектировании приводов машин. Для проверки эффективности работы новых схем в реальных приводах были изготовлены четыре модели механизмов и экспериментальная установка с измерительным комплексом.

Методика исследования
и оборудование

Модели дифференциалов изготовлены для обобщенного анализа и не связаны с конкретными приводами машин (рис. 1). Для всех схем принят прямолинейный ход 120 мм, который позволил при Zmin = 20 мм принять модуль m = 1,5 мм. В результате анализа возможных вариантов рассчитан эксцентриситет е = 30 мм для всех моделей, а величину отклонения радиусов сателлита и центрального колеса Δ (рис. 2) приняли с таким условием, чтобы оно имело общие сомножители с величиной е:

Схема 1 – Δ = + 15 мм,

Схема 2 – Δ = –15 мм,

Схема 3 – Δ = – 45 мм,

Схема 4 – Δ = – 75 мм.

Значения чисел зубьев колес и передаточное число замыкающей ступени моделей по схемам даны в табл. 1.

Для испытания моделей собрана исследовательская установка (рис. 3) не промышленного изготовления.

Рис. 1. Внешний вид моделей механизмов, по схемам 1, 2, 3, 4 слева направо и схема

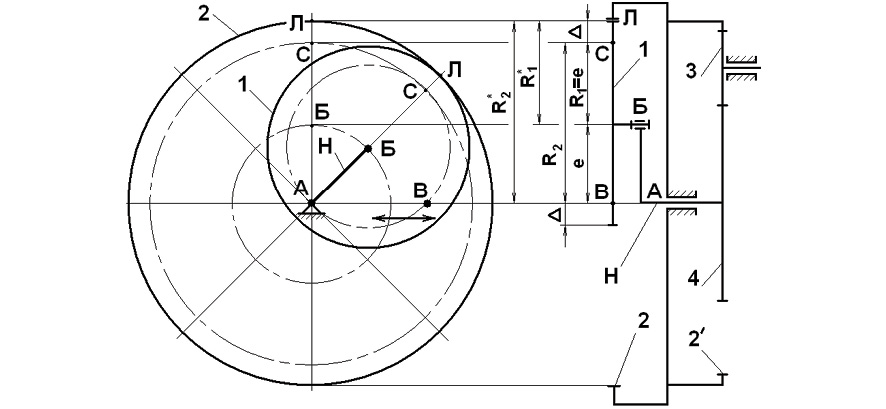
Рис. 2. Схема с обозначениями размеров на примере модели №1

Таблица 1

Параметры моделей для исследования

Рис. 3. Внешний вид экспериментальной установки и измерительного комплекса

Она состоит из рамы 1, каретки с датчиками движения 2, электродвигателя 3, редуктора 4, приводного вала 5 (жесткая пальцевая муфта, втулочные муфты, валы-удлинители), датчика крутящего момента 6, питающего элемента 7. Измерительная аппаратура (рис. 3) состоит из тензометрической станции А17-Т8, предназначенная для регистрации активных электросигналов с датчиков по 8-ми каналам одновременно, переносного компьютера для регистрации осциллограмм, часового тахометра и прибора контроля электросигнала.

Использованы самодельные датчики: перемещения подвижной каретки – реостатного типа, датчик линейной скорости – индукционного пассивного типа, датчик крутящего момента – тензометрический.

Результаты исследования

Для проверки условий существования прямой траектории в моделях получена картина обкатывания мнимой окружности на сателлите с радиусом е по геометрическому месту центров скоростей 2-го звена с радиусом 2е, как в базовом планетарном механизме (рис. 4).

Рис. 4. Картина обкатывания
мнимых окружностей

В соответствии с расчетами, обобщенная погрешность для радиусов схемы дифференциала равна:

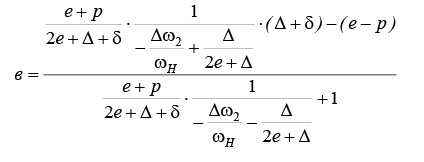
где в – ошибка в размере радиусов R и r.; δ – величина изменения Δ; р – зазор в подшипниках опор; Δω2 – приращение угловой скорости центрального колеса.

Для всех ошибок, включая ошибку положения k точки на сателлите, траектория точки В описывается координатами гипоциклоиды:

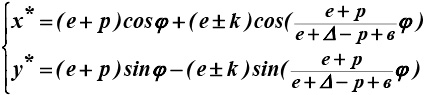
При обнулении ошибок, кроме k, получаем уравнение эллипса (рис. 5):

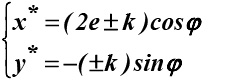
Уравнение показывает, что малая ось эллипса равна 2k, так как при обратном ходе получаем (–sin φ). А сам ход может быть короче или длиннее.

Исследование траектории точки на сателлите на прямолинейность выполнено методом киносъемки и методом вычерчивания траектории (рис. 5). При округлении числа зубьев колес замыкающей ступени образуется гипоциклоида (рис. 6).

Рис. 5. Формы траектории при наличии k – теоретическая сверху, экспериментальная снизу

а)

б)

в) г)

Рис. 6. Фотокартина положений и рисунки форм прямолинейной траектории точки:
а – фотокартина траектории движения точки; б – нормативная прямолинейная траектория;
в – гипоциклоида при отклонении в 1 зуб; г – при отклонении в 3 зуба

Теоретически получены уравнения моментов на потенциальных ведущих валах звеньев 2, 3, Н с учетом КПД шарниров ηш и зацеплении ηзуб:

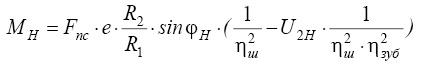
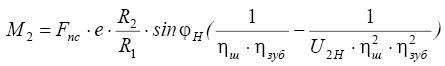
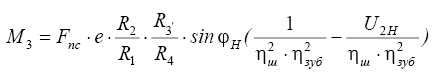
Рассмотрен также вариант с дополнительными моментами М2ДОП и М3ДОП, действующими извне на центральное колесо 2 и на замыкающий блок 3:

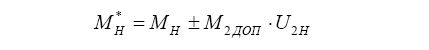
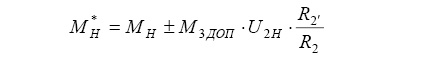
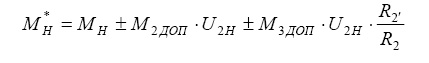
Кинематику исследовали визуально по картинам траекторий и осциллограммам перемещения и скорости точки точного прямолинейного движения. Осциллограммы изменения перемещения и скорости прямолинейного движения точки на сателлите записаны одновременно через тензометрическую станцию А17-Т8. (рис. 7).

Момент кручения так же записывался тензостанцией для всех моделей вместе с кинематикой. Анализ сходимости моментов с расчетом показан в таблице 2. Средняя сходимость результатов составила 11,3 %.

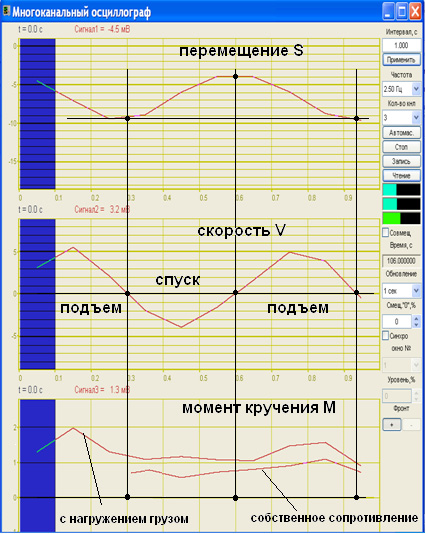
Рис. 7. Пример записи сигналов кинематики прямолинейного движения

Таблица 2

Анализ крутящего момента на водиле моделей

* – модель №4 проворачивалась через вал колеса №2

Выводы

В результате экспериментальных исследований:

– подтверждены наличие мнимой окружности качения сателлита, и формирование прямолинейной траектории без направляющей;

– показано, что кинематика соответствует гармоническому;

– показано, что при появлении ошибки в положении точки прямолинейного движения образуется стабильный эллипс;

– при округлении числа зубьев замыкающей ступени даже на один зуб появляется гипоциклоида с растущим нарушением прямой траектории;

– со средней ошибкой в пределах 11,3 % подтверждены уравнения моментов на ведущих валах Н, 2 и 3;

– показано, что модель № 4 [4] не проворачивается через водило Н из-за самоторможения. Меньшее сопротивление прокручиванию на валах замыкающей ступени 3 и центрального колеса 2.

Библиографическая ссылка