Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Григорьев И.Ю. 1 Ивашов Е.Н. 1 Панфилова Е.С. 1

---

1 ФГАОУ ВПО «Московский институт электроники и математики Национального исследовательского университета Высшая школа экономики»

Приведены главные особенности и основы проектирования устройств, которые позволяют осуществлять возвратно-вращательное (сканирующее) движение исполнительного элемента электромеханиечского привода, что даёт возможность выбрать оптимальный тип устройства.

Статья в формате PDF

891 KB

механизм сканирования

электропривод.

1. Артоболевский И.И.Теория механизмов и машин. – М.: Наука, 1988. – 640 с.

2. Зиновьев В.А. Курс теории механизмов и машин. – М.: Наука, 1972. – 384 с.

3. Крайнев А.Ф. Словарь-справочник по механизмам. – М., 1987.

4. Рощин Г.И. Несущие конструкции и механизмы РЭА. – М.: Высшая школа, 1981. – 375 с.

В технологическом оборудовании, устройствах сканирования (обзора) различных систем связи, наблюдения и контроля возникает задача создания электромеханического привода, имеющего мощность до 600 Вт, обеспечивающего возвратно-вращательное движение исполнительного элемента. В этом случае структура механических составляющих электропривода имеет вид, показанный на рис. 1а.

а)

б)

Рис. 1. Сканирующий электропривод

а) общая структура (ЭД – электродвигатель, ИЭ – исполнительный элемент)
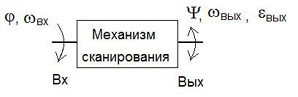
б) устройство сканирования

Здесь важным элементом электропривода является механизм сканирования (рис. 1б), который обеспечивает преобразование однонаправленного вращения входного звена в требуемое возвратно-вращательное движение выходного звена (исполнительного элемента), так как в таких приводах редуктор выполняет общеизвестные функции. При этом представляют интерес выбор конструкции механизма сканирования, анализ его кинематики и динамики.

При исследовании кинематики и динамики механизмов удобно скорости и ускорения звеньев (и их точек) выражать в зависимости от координаты (в данном случае – угловой) входного звена. Например, если определена функция положения механизма Ψ(φ) – зависимость угла поворота выходного звена – Ψ от угла поворота входного звена – φ, то угловая скорость выходного звена в любой момент времени может быть представлена в следующем виде:

,

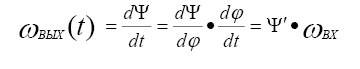где ωВХ – угловая скорость входного звена, рад/с; Ψ′ – безразмерная величина, которую называют аналогом угловой скорости выходного звена; если учесть, что в большинстве механизмов входное звено вращается равномерно ωВХ=const(t), то зависимость Ψ′(φ) позволяет оценить изменение скорости выходного звена от времени.

Аналогично, угловое ускорение выходного звена

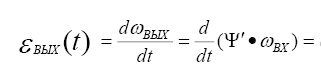
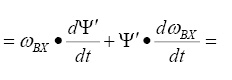
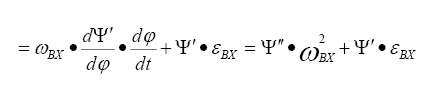
Здесь: εВХ – угловое ускорение входного звена, рад/с2; Ψ′′ – безразмерная величина, которую называют аналогом углового ускорения выходного звена.

Теоретически, с помощью сканирующего механизма можно получать самые различные законы движения выходного звена, но на практике используют только такие, которые обладают лёгкостью получения и удовлетворяют кинематическим и динамическим требованиям.

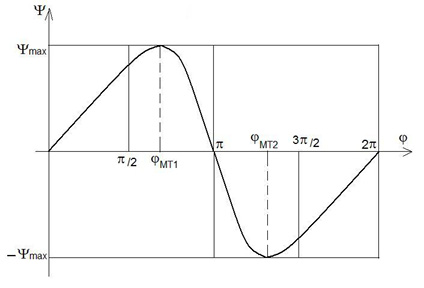
В общем виде функция положения для сканирующего механизма может быть представлена графиком, показанным на рис. 2.

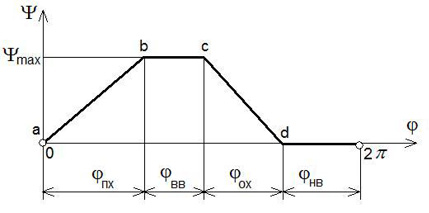
Рис. 2. Функция положения
сканирующего механизма в общем виде

На этом графике φПХ, φОХ, φВВ, φНВ, – соответственно углы прямого хода, обратного хода, верхнего выстоя и нижнего выстоя выходного звена; суммы этих углов определяют полный оборот входного звена вокруг своей оси. В системах сканирования обычно φВВ = φНВ и эти углы стараются сделать минимально возможными. Для технологического оборудования, где имеются медленный рабочий ход и быстрый холостой ход исполнительного элемента, часто делают так, чтобы φПХ > φОХ. Для систем обзора используют симметричный цикл: φПХ = φОХ.

Если функция положения на участках a-b и c-d будет линейной, то скорость выходного звена на этих участках постоянна. На рис. 3 показаны графики функции положения и аналога скорости для этого случая. Из графика аналога скорости видно, что в точках a, b, c, d возникают очень большие ускорения выходного звена (их реальная величина определяется жесткостью звеньев). Следствием этого является возникновение ударных нагрузок в механизме, что снижает его надёжность и повышает износ кинематических пар.

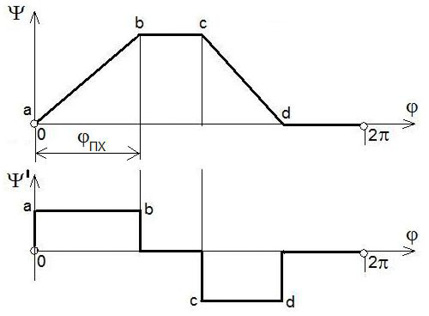
Рис. 3. Функция положения с линейными участками прямого и обратного хода

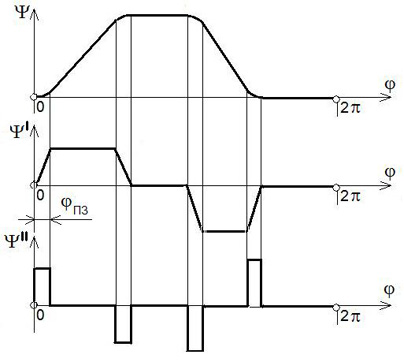
Для смягчения ударов в районе точек a, b, c, d делают переходные зоны φПЗ ≈ 0,15φПХ (рис. 4а), которые смягчают ударные нагрузки и позволяют решить эту проблему для тихоходных механизмов.

В положениях выходного звена (исполнительного элемента), где оно движется с ускорением εИЭ, на него действуют моменты сил инерции МДИН=JИЭ∙εИЭ, где JИЭ – момент инерции исполнительного элемента. Избежать сильных ударных нагрузок, что является весьма важным для быстроходных механизмов, можно при использовании треугольной (или синусоидальной) формы графика аналога ускорений (рис. 4б).

В узлах сканирования наиболее часто применяются кривошипно-коромысловые, кривошипно-кулисные и кулачково-коромысловые механизмы [1-3]. Каждый из них характеризуется комплексом свойств и особенностей, которые следует учитывать при проектировании.

а)

б)

Рис. 4. Функция положения механизма сканирования:

а) со смягчением ударных нагрузок
б) с малыми ударными нагрузками

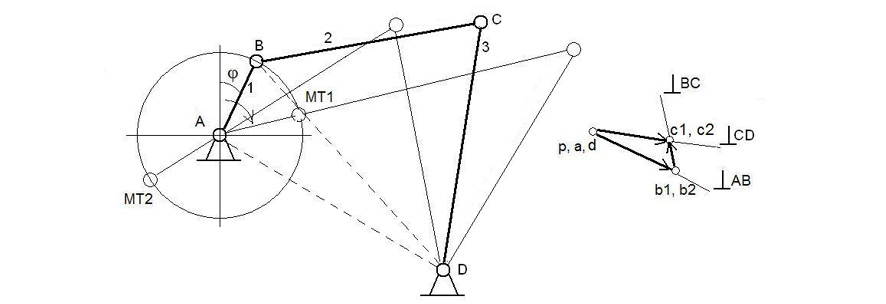
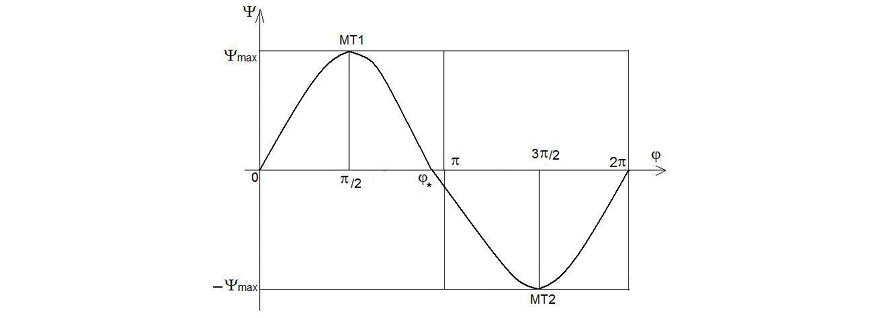
Кривошипно-кулисный механизм и план скоростей для него в выделенном положении представлены на рис. 5а. В положениях МТ1 и МТ2 – «мёртвых точках» – наблюдается остановка кулисы. Из рисунка видно, что

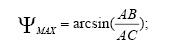
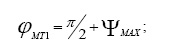
Важным преимуществом такого механизма является его компактность и простота конструкции. Прямой и обратный ход кулисы неодинаковы, поэтому рабочий ход (медленный) делают на участке от МТ2 до МТ1, а холостой ход (быстрый) на участке от МТ1 до МТ2. Кулиса здесь движется неравномерно. Примерный вид функции положения для изображенного на рис. 5а механизма показан на рис. 5б.

Выполним аналитический расчёт кинематики такого механизма. Рассмотрим треугольник АВС. В проекциях на оси координат x и y получим уравнения:

на ось x ABcosφ + AC = BCcosΨ, (1)

на ось y ABsinφ = BCsinΨ . (2)

Разделим (2) на (1):

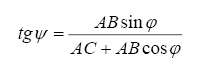
Тогда функция положения будет

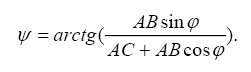
Если продифференцировать уравнение (2) по координате φ, то получим

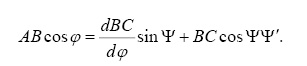
Из углов этого уравнения вычтем угол Ψ (то есть, применим метод обращения движения) и получим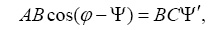  

откуда аналог скорости кулисы будет

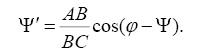
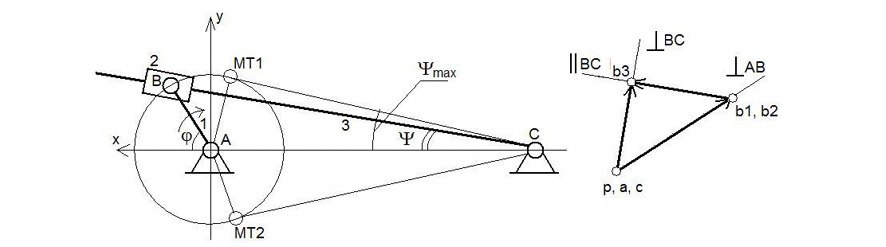
Рис. 5. Кривошипно-кулисный механизм: а) схема механизма и план скоростей

б)

Рис. 5. Кривошипно-кулисный механизм:
б) функция положения

В общем виде кривошипно-коромысловый механизм выглядит так, как показано на рис. 6а. При равномерном вращении кривошипа АВ коромысло CD совершает неравномерные качания относительно точки D.

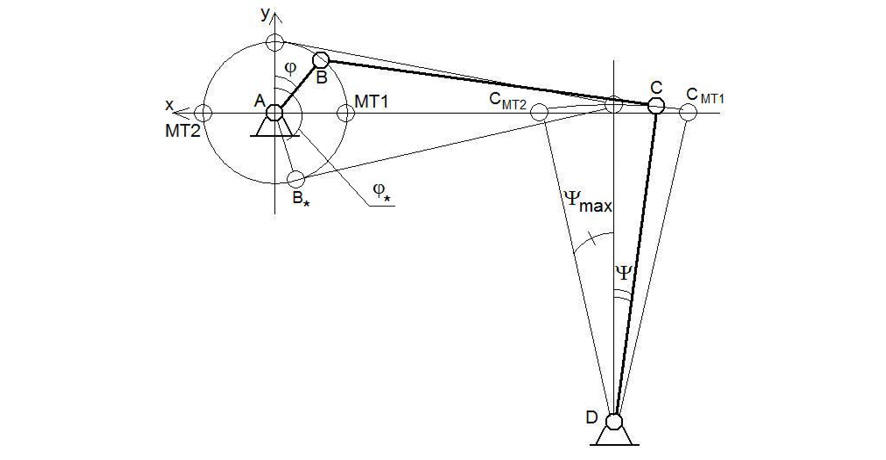
Представляет интерес частный вид кривошипно-коромыслового механизма, показанный на рис. 6б [3]. За половину оборота кривошипа коромысло совершает полное качание в одну сторону. Амплитуда качания коромысла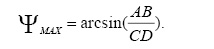  

Функция положения показана на рис. 6в). Из графика функции положения механизма видно, что качания коромысла в одну и в другую стороны почти идентичны (особенно, если длина кривошипа AB мала по сравнению с BC и CD.

Аналитический анализ кинематики кривошипно-коромыслового механизма (рис. 6а) можно выполнить, рассматривая сначала треугольник ABD (определить зависимость BD как функцию угловой координаты кривошипа), а затем треугольник BDC с использованием известных теорем планиметрии: теорем косинусов и синусов. В результате будет получена вычисляемая с большой точностью функция положения механизма. Подробно этот метод изложен в [1].

Кулачково-коромысловый механизм – механизм, ведущее звено которого – кулачок, имеющее поверхность переменной кривизны, взаимодействует с другим подвижным звеном – коромыслом, образуя высшую кинематическую пару (соприкосновение по линиям и точкам). Кулачки можно изготавливать дисковыми или цилиндрическими, а силовое замыкание между кулачком и коромыслом осуществляется упругим элементом (пружиной) или с помощью жёлоба.

Выбирая профиль кулачка, можно получить практически любой закон движения коромысла при равномерном вращении кулачка. Часто требуется получить линейную функцию положения коромысла на этапе его подъёма или опускания (рис. 3). В этом случае профиль кулачка на этом участке представляет собой фрагмент спирали Архимеда (её радиус: R = A∙φ, где A = const).

На рис. 7а показан механизм сканирования с дисковым кулачком, а на рис. 7б – план скоростей для указанного положения. При вращении кулачка изменяется угол давления − υ, угол между нормалью n-n к профилю кулачка в данном положении и направлением П, перпендикулярным к коромыслу (рис. 7а). Когда υ > υMAX ≈ 45O, то проекция силы давления коромысла F2N = F2sin υ становится весьма большой, из-за чего возникают значительные потери на трение (вплоть до заклинивания и самоторможения) и значительный износ в шарнирах. Если увеличить минимальный радиус кулачка − r0, то скорость точки В кулачка увеличится (VB1=ω1∙AB). Поэтому план скорости для одного и того же положения кулачка и при неизменном значении аналога скорости коромысла изменится как показано на рис. 7в. Из сравнения двух планов (рис.7б и в) следует, что с увеличением габаритных размеров кулачка (минимального радиуса − r0) при неизменной кинематике механизма угол давления уменьшается (υ′< υ).

При кинематический анализе кулачково-коромыслового механизма, показанного на рис. 7а, для определения функции положения коромысла при вращении кулачка с заданным профилем можно применить широко распространённые графические методы [1, 2].

Для снижения трения часто в точке В коромысла устанавливают вращающийся ролик радиусом rР. В этом случае реальный профиль кулачка выполняют по кривой, эквидистантной полученному профилю и расположенной на расстоянии rР от него (рис. 8б). Если силовое замыкание между кулачком и коромыслом обеспечивается пружиной (рис. 8б), то надо выбирать пружину достаточно жёсткой, чтобы не могло произойти размыкания между звеньями. С другой стороны, слишком жёсткая пружина увеличивает износ трущихся элементов механизма. Для пружины должно выполняться условие МПР МАХ ≈ (1,2…1,3)МДИН МАХ, где МПР МАХ – максимальный момент, развиваемый пружиной; МДИН МАХ – максимальный динамический момент коромысла МДИН МАХ = JКОР∙εКОР МАХ, JКОР – момент инерции коромысла, εКОР МАХ – максимальное угловое ускорение коромысла на участке его опускания. Можно использовать и геометрическое замыкание между кулачком и коромыслом (рис. 8в) с помощью жёлоба или канавки на кулачке. Но в этом случае изготовление кулачка сильно усложняется.

а)

б)

в)

Рис. 6. Кривошипно-коромысловый механизм:

а) общий случай б) частный случай в) функция положения для механизма рис.6б

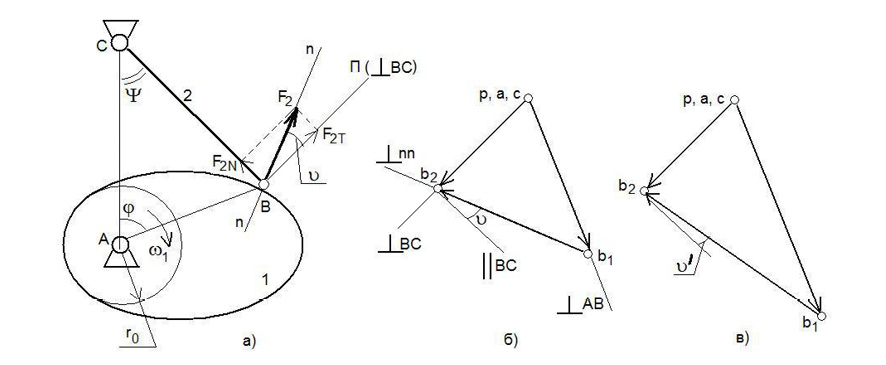
Рис. 7 Дисковый кулачково-коромысловый механизм

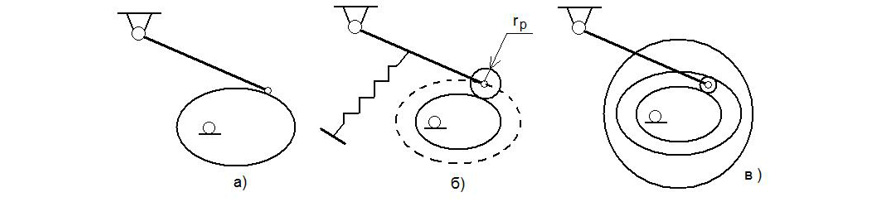
Рис. 8. Модификации кулачкового механизма

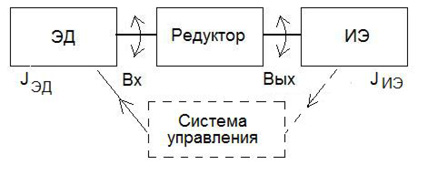
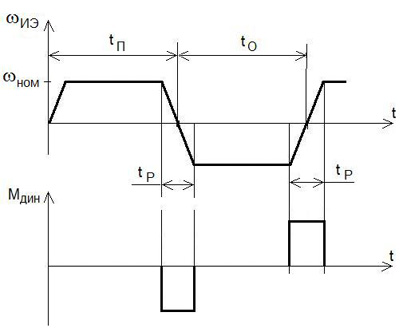
Электропривод, выполняющий сканирующие функции, можно сделать намного компактнее, если за счёт системы управления обеспечить быстрое и надёжное реверсирование ротора электродвигателя в процессе его работы. В этом случае структура механических элементов электропривода, по сравнению с изображённой на рис. 1, станет более простой (рис.9а), но возникнет необходимость в усложнении системы управления приводом, которую надо дополнить функцией реверса. Преимущество такой схемы, помимо компактности, заключается ещё и в том, что в ней можно реализовать движение исполнительного элемента с постоянной скоростью на всём этапе движения от одной крайней точки его положения до другой (рис. 3). Однако схема с реверсированием двигателя имеет ряд недостатков [4]. Во-первых, если не использовать сложную систему управления, то прямой и обратный ход выходного звена совершается при одной и той же частоте ротора двигателя, а это означает, что продолжительность прямого и обратного ходов будет одинаковой, что не является приемлемым для ряда технологических процессов. Во-вторых, в крайних точках положения выходного звена система управления должна осуществить быстрое реверсирование ротора электродвигателя. Этот переходный процесс (он показан на рис. 9б) занимает какое-то время – время реверса (обычно его лимитируют на уровне до 10% от продолжительности прямого или обратного хода исполнительного элемента) и сопровождается возникновением значительных динамических инерционных нагрузок в электроприводе. Величина возникающего на валу двигателя динамического момента будет определяться угловым ускорением ротора электродвигателя при реверсировании – εЭД и приведённым к валу электродвигателя моментом инерции – JПР: МЭД ДИН = JПР∙εЭД, Н∙мм. Здесь

, ,

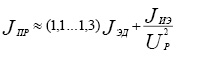
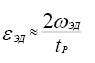
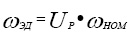
где JЭД, JИЭ – моменты инерции ротора двигателя и исполнительного элемента, Н∙мм∙с2; UР – передаточное отношение редуктора, ωЭД – номинальная угловая скорость вращения ротора, рад/с, при движении исполнительного элемента с номинальной угловой скоростью ωНОМ (рис. 9б), tР – продолжительность этапа реверсирования, с. При частых реверсах и значительных динамических моментах двигатель работает в тяжелом режиме (перемежающаяся нагрузка), что приводит к его перегреву, а все узлы трения привода подвергаются значительному износу.

а)

б)

Рис. 9. Реверсируемый сканирующий электропривод: а) структура привода
б) диаграммы скорости и динамического момента

Это неприятное явление может быть значительно ослаблено за счёт применения в электроприводе двух управляемых сцепных муфт, осуществляющих реверсирование исполнительного элемента при неизменном направлении вращения ротора двигателя (рис. 10). Сцепная муфта в зависимости от управляющего сигнала жестко соединяет или полностью разъединяет установленные на ней колесо К и шестерню Ш. Система управления электропривода поочерёдно подаёт управляющий сигнал на одну из муфт М1 или М2, в результате чего исполнительный элемент вращается либо непосредственно от выходной шестерни редуктора (муфта М1 – включена, а муфта М2 – отключена), либо через паразитное колесо, роль которого выполняет колесо К1 муфты М1, когда муфта М1 – отключена, а муфта М2 – включена. Сцепные муфты здесь могут быть как фрикционные, так и порошковые. В фрикционных сцепных муфтах соединение полумуфт (колеса К и шестерни Ш) осуществляется за счёт сил трения, а разъединение – благодаря электромагниту, раздвигающему фрикционные диски между ними. Иногда для увеличения передаваемого муфтой момента фрикционные поверхности заменяют торцовыми зубьями, но в этом случае срабатывание муфты происходит дольше и более жёстко (сопровождается микроударами). В порошковых сцепных муфтах полумуфты соединяются за счёт вязкой массы, состоящей из ферромагнитного порошка и смазочной жидкости. При отсутствии напряжения вязкость массы небольшая и полумуфты механически не связаны. При подаче управляющего сигнала ферромагнитные частицы намагничиваются и вязкость массы увеличивается, механически связывая полумуфты. При этом соединение происходит очень быстро (за 0,005…0,05 секунды) и мягко. К сожалению, со временем частицы порошка изнашиваются, поэтому ресурс таких муфт невелик.

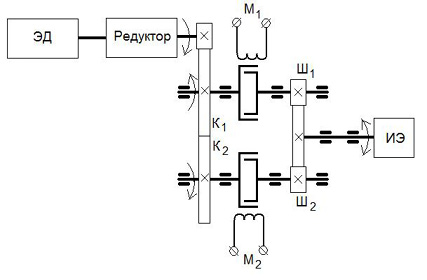
Рис. 10. Реверсивный электропривод
со сцепными муфтами

Подводя итог, можно отметить, что существует целый ряд различных конструктивных решений, обеспечивающих возвратно-вращательное движение исполнительного элемента, каждый из которых обладает своими особенностями. Для экспресс-выбора типа механизма эти особенности в укрупнённом виде можно свести в единую бинарную таблицу, где наличие указанного признака отмечено цифрой 1, а отсутствие – цифрой 0 (табл.1). Для более полного анализа при принятии решения необходимо проводить тщательный анализ различных конструкций с подбором их параметров и последующим сравнением полученных вариантов.

Таблица 1

Конструктивные особенности механизмов с возвратно-вращательным движением исполнительного элемента (ИЭ)

Библиографическая ссылка