На практике часто возникает необходимость провести анализ данных, представляющих собой нелинейную зависимость двух переменных. Нужно определить вид их функциональной связи и построить регрессионную модель, выравнивающую опытные данные. Для этого используют метод линеаризации модели. Данный метод основан на нахождении замены переменных, которая преобразует нелинейные уравнения в линейные, что в конечном итоге позволяет применять теорию линейной регрессии для построения нелинейной модели. Применение линеаризации модели позволяет лучше разобраться в качественных и количественных особенностях нелинейной системы. Так, например, можно определить вид зависимости коэффициента теплоотдачи (Y), от горизонтальной стенки к кипящей воде от разности температур стенки и кипящей воды (X):
|
X |
6,10 |
7,50 |
8,88 |
11,10 |
12,20 |
|
Y |
3185 |
5390 |
6860 |
10045 |
12740 |
Значительное число нелинейных зависимостей, встречающихся в химической практике, может быть описано следующими уравнениями:
y=a·bx; (1)
y=a·xb; (2)
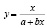 . (3)
. (3)
Первое и второе уравнения легко привести к линейному виду, прологарифмировав их:
lny=lna+x·lnb=>Y=A+Bx,
где Y=lny, A=lna, B=lnb;
lny=lna+b·lnx=>Y=A+bX,
где Y=lny, A=lna, X=lnx.
Для приведения третьего уравнения к линейному виду нужно выполнить преобразование:
y=x/(a+bx) => x/y=a+bx => Y=a+bx,
где Y=x/y.
Вычислив для каждого уравнения (1)-(3) парные коэффициенты корреляции (0,986574) (0,995185) и (–0,93835) соответственно, приходим к выводу что модель (2) наилучшим образом характеризует рассмотренную зависимость, так как величина коэффициента корреляции для нее наивысшая. Проводим замену переменных Y=lny, A=lna, X=lnx. Теперь уравнение имеет вид: Y=A+bX. Вычислив параметры регрессии, приходим к модели вида: y=106,627·x1,9067. Подставляя значения xi в полученное уравнение регрессии, найдем значения коэффициента теплоотдачи, выравнивающие опытные данные:
|
X |
6,1 |
7,5 |
8,88 |
11,1 |
12,2 |
|
Y |
3185 |
5390 |
6860 |
10045 |
12740 |
|
Yвыравн. |
3351,782 |
4970,141 |
6858,515 |
10495,68 |
12567,72 |
Построенная по вычисленным данным диаграмма представлена на рисунке.
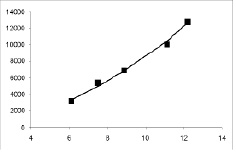
Диаграмма рассеяния и выравнивающая опытные данные линия регрессии
Полученная регрессионная модель хорошо отражает функциональную зависимость коэффициента теплоотдачи от стенок сосуда к кипящей воде.
Библиографическая ссылка
Мотченко А.О., Мухамбетов Е.Ю., Антипина С.Г. ИЗУЧЕНИЕ ЗАВИСИМОСТИ КОЭФИЦЕНТА ТЕПЛООТДАЧИ ОТ СТЕНОК СОСУДА К КИПЯЩЕЙ ВОДЕ // Современные наукоемкие технологии. 2014. № 5-2. С. 226-227;URL: https://top-technologies.ru/ru/article/view?id=34090 (дата обращения: 05.03.2026).



