Сушка – термический процесс принудительного удаления жидкости из твёрдых, жидких веществ или их смесей с помощью испарения. Чаще всего в качестве удаляемой жидкости выступают влага или летучие органические растворители. При сушке изменяется теплопроводность материала, снижается его объемный вес и повышается прочность. Чем выше качество материала, тем больше возможность его использования. Это может быть обеспечено при соответствующем режиме процесса сушки, который должен проводиться при определенной температуре, давлении и относительной влажности сушильного агента. Режим сушки зависит от свойств высушиваемого материала. Сушка широко применяется в химической, химико-фармацевтической, пищевой и других отраслях промышленности. В химической промышленности сушка обычно является завершающим процессом в производстве почти всех химических продуктов.
Цель сушки – улучшение качества веществ и материалов, подготовка их к переработке, использованию, транспортированию и хранению. Данный процесс часто является последней технологической операцией, предшествующей выпуску готового продукта. Именно поэтому оценка эффективности работы сушильного аппарата играет очень важную роль.
В ходе проведения эксперимента были получены следующие данные:
|
х |
0 |
20 |
40 |
60 |
80 |
100 |
|
у |
29,5 |
18,4 |
11,9 |
8,6 |
5,0 |
3,3 |
Признак х – время сушки в с, признак у – содержание влаги, в % от веса сухого остатка.
Определим вид функциональной зависимости, отражающий влияние времени сушки в секундах на вес сухого остатка.
Построим график зависимости величин х и у. Мы видим, что зависимость получается нелинейной. Построив же график зависимости х и lnу, наблюдаем расположение точек вдоль некоторой прямой. Т.е. при Y = lnу линейное уравнение Y = А + Вх отражает нелинейную зависимость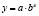 
, где 
.
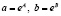Определим значение коэффициентов А и В. Вычислим числовые характеристики: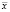 
= 50,00167; ȳ = 2,288067; Sx2= 1679,76; Sxy = – 30,3695. Тогда 
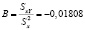, A =ȳ – В ∙ 
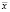= 3,192081. Запишем уравнение линейной регрессии: Y = 3,192081х – 0,01808. Тогда уравнение нелинейной регрессии будет иметь вид: у = 24,33902 ∙ 0,982083х. Подставив значения хᵢ в полученное уравнение, найдем значения ỹᵢ, выравнивающие экспериментальные данные. Построим диаграмму рассеяния и полученную линию регрессии.
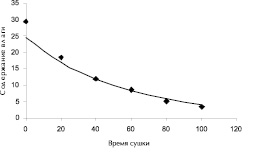
Полученная модель позволяет определять значения содержания влаги в зависимости от времени сушки для любых начальных данных. Однако, не следует брать значения для прогноза, выходящие за рамки размаха вариационного ряда более чем на 10-15 %, так как в этом случае ошибка прогноза резко возрастает.
Библиографическая ссылка
Звада А.А., Каткова Д.А., Антипина С.Г. ОЦЕНКА ЭФФЕКТИВНОСТИ РАБОТЫ СУШИЛЬНОГО АППАРАТА // Современные наукоемкие технологии. – 2014. – № 5-2. – С. 223-224;URL: https://top-technologies.ru/ru/article/view?id=34087 (дата обращения: 20.04.2024).