В настоящее время в различных областях современной науки широко применяется компьютерное моделирование (КМ). В физической химии, например, КМ позволяет исследовать структуру и свойства материалов. Широко применяемый в физической химии метод модекулярной динамики (МД) позволяет определить целый комплекс свойств (структурные, термодинамические, транспортные) и исследовать взаимосвязи наноструктуры и физико-химических свойств.
Важной характеристикой при МД-моделировании является размер (количество частиц) моделируемой системы. С увеличением числа частиц до 106 линейные размеры модельного куба достигают нанометров, что позволяет получать результаты нового качества, обладающих практической значимостью. Увеличение числа частиц моделируемой системы требует серьезных временных затрат на проведение КМ, что делает невозможным проведение КМ без привлечения высокопроизводительных вычислений.
Для проведения параллельного расчета системы N-частиц широко применяется вычислительный кластер, состоящий из вычислительных узлов(вычислителей) объединенных каналами связи. В большинстве случаев рассчитываемое множество частиц разбивается на одинаковые подмножества между вычислительными узлами кластера для проведения параллельного расчета. Но возникают ситуации, когда на кластерных системах вычислители обладают разной производительностью. Это означает, что время проведения КМ будет равно времени завершения своего расчета самым слабым (по производительности) узлом кластера.
Для обеспечения одновременного завершения расчетов всеми вычислителями, разработана модель балансировки нагрузки для параллельного расчета системы N-частиц на гетерогенной кластерной системе, что позволит существенно сократить время КМ.
Для определения размеров подмножеств частиц используется процентная доля производительности каждого из вычислительных узлов кластера, в соответствии с которой рассчитывается число частиц, направляемое вычислителю для расчета. Формула для вычисления мощности подмножества частиц, направляемых каждому вычислителю в зависимости от его производительности:
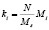 (1)
(1)
где ki – подмножество частиц направляемых для расчета вычислителю Pi, N – множество частиц в системе, Mi – производительность i-го вычислителя P, Ms – суммарная мощность всех вычислителей в системе.
На рисунке представлен алгоритм распределения нагрузки между вычислителями в соответствии с мощностями каждого вычислителя.
Определение мощности подмножества дескрипторов производится в тестовом режиме до начала моделирования системы N-частиц. Главный вычислитель проверяет готовность всех подчиненных вычислителей и передает для тестового расчета одинаковые подмножества дескрипторов {Dls(i)} и {Dlv(i)}. С учетом времени расчета каждым вычислителем своего подмножества дескрипторов главный вычислитель определяет мощность подмножества для каждого вычислителя по формуле (1). Вновь сформированные подмножества будут передаваться вычислителям во время процесса моделирования.
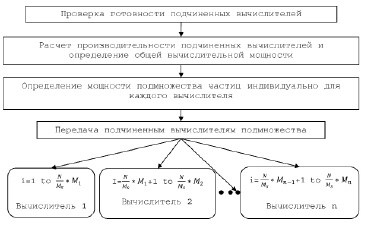
Алгоритм распределения нагрузки между вычислителями в соответствии с производительностью каждого вычислителя.
Для оценки эффективности разработанной модели распределенных вычислителей проведено тестовое моделирование системы оксид кремния SiO2 в программном комплексе ИИС «MD-SLAG-MELT»[5]. Тестирование проходило на 16 вычислителях AMD и Intel разной производительной мощности. В моделирование сравнивалось время, затраченное на проведение эксперимента с числом частиц в системе 105 и числом шагов 5000. Результаты компьютерных экспериментов показаны в таблице.
Результаты тестового моделирования системы SiO2 (в часах)
|
N Метод загрузки |
1000 |
4200 |
12000 |
100000 |
|
Равномерная загрузка |
0,9 |
1,75 |
3,7 |
11,5 |
|
Загрузка по вычислительным мощностям |
0,42 |
0,81 |
2,9 |
9,4 |
Таким образом, использования модели балансировки нагрузки позволит в равной степени задействовать все вычислители на максимальную мощность в течении всего времени выполнения моделирования системы N-частиц. Данный подход обеспечивает наиболее равномерное распределение нагрузки между вычислителями, т.к. позволяет гибко регулировать объемы обрабатываемых подмножеств и обеспечивает эффективность работы всей системы приближенную к оптимальной, что не позволяют обеспечить ранее описанные методы для гетерогенной вычислительной среды. Кроме того, данная модель позволяет обеспечить оптимальную эффективность использования вычислителей, как для гетерогенной, так и для однородной среды.
Библиографическая ссылка
Пилипчак П.Е., Воронова Л.И., Трунов А.С. МОДЕЛЬ БАЛАНСИРОВКИ НАГРУЗКИ ДЛЯ ПАРАЛЛЕЛЬНОГО РАСЧЕТА СИСТЕМЫ N-ЧАСТИЦ НА ГЕТЕРОГЕННОЙ КЛАСТЕРНОЙ СИСТЕМЕ // Современные наукоемкие технологии. 2014. № 5-2. С. 218-219;URL: https://top-technologies.ru/ru/article/view?id=34082 (дата обращения: 05.03.2026).



