Численное решение систем линейных алгебраических уравнений (СЛАУ) – одна из наиболее часто встречающихся задач в научно-технических исследованиях, математической физике, экономике, статистике. Все используемые на практике методы решения СЛАУ можно разделить на две группы: точные методы и итерационные методы.
Преимуществом итерационных методов является удобное применение в современной вычислительной технике, т.к. решения, полученные с помощью прямых методов, обычно содержат погрешность. Итерационные методы же позволяют получить решение данной системы с заранее заданной точностью.
Суть итерационных методов решения систем заключается в том, что СЛАУ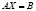 
мы приводим к итерационной форме 
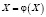. Задаем начальное приближение значений решений 
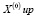решение системы ищем в виде последовательности 
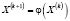, постепенно улучшающихся приближений. Итерационный процесс должен быть сходящимся и его продолжают до тех пор, пока два последовательных приближения не совпадут в пределах заданной точности. Примером обычных итерационных методов служат: метод итераций (метод Якоби), метод Зейделя, метод верхних релаксаций.
Мы подробнее остановимся на итерационном методе Зейделя, т.к. этот метод является одним из самых распространенных и наиболее легко программируемых.
Он представляет собой некоторую модификацию метода простых итераций. Идеей этого метода, а самое главное его особенностью является то, что полученное в первом уравнении значение сразу же используется во втором, а значения первого и второго – в третьем и т. д. Итерационный процесс продолжается до тех пор, пока значения неизвестных не станут отличаться от предыдущих приближений на заданную точность ε.
Мы рассмотрели применение метода Зейделя к решению системы
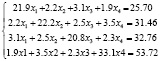
с точностью ε = 0,0001.
В данной системе наблюдаем преобладание диагональных коэффициентов, что является достаточным условием сходимости метода Зейделя. Приведем систему к виду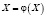 
и запишем итерационную формулу
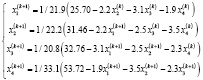
В ходе работы была написана программа в среде программирования C++ по реализации решения СЛАУ методом Зейделя. В качестве начального вектора выбрали свободные члены системы: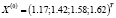 
. Оказалось, что достаточно трех итераций, чтобы получить решение данной системы с заданной точностью. В итоге мы получили следующий вектор решений 
.
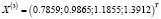Явным преимуществом итерационных методов является значительное превосходство над точными методами по скорости, и они удобнее реализуются на практике. Использование итерационных методов с помощью ЭВМ эффективно в решении СЛАУ с разряженными матрицами, а также для уточнения решения СЛАУ, полученного с помощью прямого метода. Главным недостатком этих методов является то, что вопрос сходимости итерационного процесса требует отдельного исследования.
Библиографическая ссылка
Савина Н.С., Зленко О.А., Матвеева Т.А., Агишева Д.К. РЕШЕНИЕ СЛАУ ИТЕРАЦИОННЫМИ МЕТОДАМИ И ИХ ПРЕИМУЩЕСТВА // Современные наукоемкие технологии. – 2014. – № 5-2. – С. 197-198;URL: https://top-technologies.ru/ru/article/view?id=34069 (дата обращения: 24.04.2024).