Очень часто для практических целей приходится обрабатывать экспериментальные данные так, чтобы по возможности точно отобразить общую закономерность зависимостиy от x, но вместе с тем сгладить случайные уклонения, связанные с неизбежными погрешностями самого наблюдения. Для решения подобных задач обычно применяется расчетный метод наименьших квадратов, разработанный знаменитыми математиками К. Гауссом и А. Лежандром.
Этот метод дает возможность при заданном типе зависимости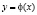 
так выбрать ее числовые параметры, чтобы сумма квадратов отклонений экспериментальных точек от сглаживающей кривой обращалась в минимум.
Мы рассмотрели применение данного метода к решению прикладной задачи: торговое предприятие имеет сеть, состоящую из 12 магазинов. Руководство предприятия хотело бы знать, как зависит размер годового товарооборота от торговой площади магазина.
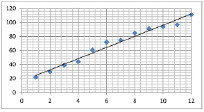
Для определения вида зависимости наших экспериментальных данных построим диаграмму рассеяния. Введем обозначения: пусть xk – площадь k-го магазина, тыс. м2; yk – годовой товарооборот k-го магазина, млн руб.
|
xk |
yk |
|
0,24 |
19,76 |
|
0,35 |
35,09 |
|
0,48 |
40,95 |
|
0,55 |
41,08 |
|
0,78 |
56,29 |
|
0,94 |
68,51 |
|
0,98 |
75,01 |
|
1,12 |
89,05 |
|
1,21 |
91,13 |
|
1,25 |
94,26 |
|
1,29 |
99,84 |
|
1,49 |
108,55 |
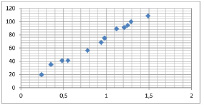
Диаграмма рассеивания экспериментальных данных
По внешнему виду данной диаграммы можно сделать выводо линейной зависимости.
В случае линейной зависимости сглаживающей кривой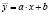 
минимизируем функцию
.
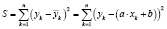Для этого необходимо, чтобычастные производные первого порядка функции по параметрам a и b равнялись нулю. В итоге получим систему линейных уравнений
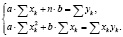
Вспомогательные вычисления производили в Excel. В нашем случае система имеет вид
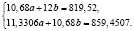
Решив её по правилу Крамера, получили неизвестные параметры a и b; и сглаживающая кривая примет вид: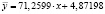 
.
Из этого следует, что при увеличении торговой площади на 1 тыс. м2 среднегодовая прибыль увеличивается на 71,26 млн руб.
Метод наименьших квадратов очень широко применяется в настоящее время в самых разных сферах жизни нашего общества. Его основным достоинством является простота и достаточно высокая точность.Хотелось бы отметить, что в результате выполнения работы данного вида мы получили навыки работы с этим методом, получили новые научные знания.
Библиографическая ссылка
Колеснёв А.С., Котин А.И., Матвеева Т.А., Зотова С.А. СГЛАЖИВАНИЕ ЭКСПЕРИМЕНТАЛЬНЫХ ЗАВИСИМОСТЕЙ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ // Современные наукоемкие технологии. – 2014. – № 5-2. – С. 193-193;URL: https://top-technologies.ru/ru/article/view?id=34065 (дата обращения: 22.11.2024).