Цель работы: описать, что представляет собой сетевое планирование и управление (СПУ); познакомить учащихся с подготовкой проекта; дать представление о методах СПУ.
Для достижения поставленной цели необходимо решить следующие задачи: познакомить учащихся с задачами СПУ и методами их решения; дать представление о графах и их применении; сформировать необходимые знания и умения для построения сетевых графиков простейших проектов и расчёта их отдельных параметров.
Для полноценного усвоения материала школьники должны знать основные элементы сетевого планирования и управления (сетевая модель, работа, событие, критический путь) и наглядные способы изображения проекта (граф, сетевой график, таблица).
Сетевая модель – это план выполнения некоторого комплекса взаимосвязанных работ, заданного в форме сети, графическое изображение которой называется сетевым графиком.
Главными элементами сетевой модели являются работы и события.
Термин работа в СПУ имеет несколько значений. Во-первых, это действительная работа – протяжённый во времени процесс, требующий затрат ресурсов (например, сборка изделия, испытание прибора и т.п.). Во-вторых, это ожидание – протяжённый во времени процесс, не требующий затрат труда (например, процесс сушки после покраски, старения металла, твердения бетона и т.п.). В-третьих, это зависимость, или фиктивная работа – логическая связь между двумя или несколькими работами (событиями), не требующими затрат труда, материальных ресурсов или времени. Продолжительность фиктивной работы равна нулю.
Событие – это момент завершения какого-либо процесса, отражающий отдельный этап выполнения проекта. Событие может являться частным результатом отдельной работы или суммарным результатом нескольких работ. Событие может свершиться только тогда, когда закончатся всё работы, ему предшествующие. Последующие работы могут начаться только тогда, когда событие свершится. При этом предполагается, что событие не имеет продолжительности и свершается как бы мгновенно.
Сначала планируемый процесс разбивается на отдельные работы, составляется перечень работ и событий, продумываются их логические связи и последовательность выполнения. Затем составляется сетевой график.
В качестве наглядного примера модели сетевого планирования и управления выбрана задача из известного всем детям произведения:
Ослик Иа решил пригласить на день рождения Винни-Пуха, Пятачка и Кролика. Однако Иа смог передать приглашение лично только Кролику, как самому умному и ответственному. Ослик решил, Кролик передаст приглашения остальным и приведёт их ко времени начала праздника. Гости приглашены на 1700. А так как Кролик был очень умный и не хотел опаздывать, то решил всё хорошо продумать. План его действий представлен в табл. 1.
Таблица 1
|
Дело |
Содержание дела |
Продолжительность (в часах) |
Предшествующие дела |
|
A |
Прийти к Пятачку |
1 |
–– |
|
B |
Передать Пятачку приглашение и подождать, пока он соберётся |
0,3 |
A |
|
C |
Рассказать Пятачку, что ослик Иа хотел бы получить в подарок |
0,1 |
B |
|
D |
Помочь Пятачку в выборе подарка |
0,5 |
A |
|
E |
Выслушать от Пятачка новости |
0,3 |
A |
|
F |
Помочь Пятачку оформить подарок |
0,3 |
C, D |
|
G |
Рассказать свои новости, чтобы не показаться недружелюбным |
0,4 |
E |
|
H |
Дойти с Пятачком до Винни-Пуха |
1,5 |
F, G |
|
I |
Сообщить Винни-Пуху о приглашении |
0,2 |
H |
|
J |
Помочь Винни-Пуху найти горшок с мёдом и собраться |
0,8 |
I |
|
K |
Ждать, пока Винни-Пух сочинит праздничную сопелку |
1 |
I |
|
L |
Дать время съесть Винни-Пуху мед из горшка |
0,4 |
J |
|
M |
Дать время придумать Винни-Пуху ответ на вопрос – «Почему горшок пустой?» |
0,5 |
L |
|
N |
Дойти от Винни-Пуха к ослику Иа |
0,5 |
J |
|
O |
Поздравить ослика Иа с Днём рождения ровно в 1700 |
0,1 |
K, M, N |
Необходимо помочь Кролику и его друзьям не опоздать на праздник. Определить самое позднее время выхода кролика из дома. На какие дела нужно обратить внимание, чтобы они не растянулись во времени?
После анализа задачи школьникам можно представить изображение таблицы в виде ориентированного графа (рис. 1). Стрелками представлены работы (дела), при этом длина стрелки никак не связана с длительностью самой работы. Пронумерованными кругами изображены события (моменты начала и окончания дел).
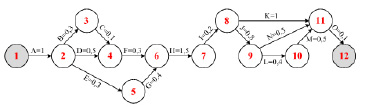
Рис. 1
В результате расчёта временных параметров (сроки начала и окончания каждого события) получим сетевую модель (рис. 2). Если значения в левом и правом секторах круга совпадают, то событие является критическим. Работы, соединяющие такие события, также являются критическим (на них надо обратить особое внимание, т.к. они не имеют резервов времени).
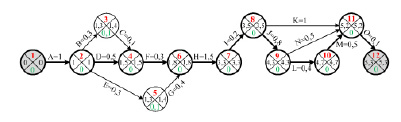
Рис. 2
На рис. 2 жирными стрелками выделен критический путь (он имеет максимально возможную длину). В нашем случае длина критического пути равна 5,3 или 5 часов 18 минут. Это означает, что Кролику следует выйти из дома не позднее 11 часов 42 минут, чтобы прийти на праздник вместе с друзьями вовремя.
Так на простом и наглядном примере можно познакомить школьников с решением серьёзных задач планирования и управления комплексами работ.
Библиографическая ссылка
Карижский С.А., Лащенов С.А., Агишева Д.К., Матвеева Т.А. СЕТЕВОЕ ПЛАНИРОВАНИЕ И УПРАВЛЕНИЕ В РЕШЕНИИ ЗАДАЧИ «ДЕНЬ РОЖДЕНИЯ ОСЛИКА ИА» // Современные наукоемкие технологии. 2014. № 5-2. С. 191-193;URL: https://top-technologies.ru/ru/article/view?id=34064 (дата обращения: 03.02.2026).



