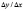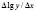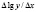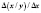Экспериментальное исследование зависимости физических величин, влияния условий на свойства и поведение исследуемых систем является весьма важной задачей в области инженерных исследований. Одним из наиболее разработанных и часто используемых для аппроксимации экспериментальных данных является метод наименьших квадратов.
В первую очередь при использовании этого метода необходимо выбрать вид функциональной зависимости между экспериментальными данными. Универсального способа выбора вида сглаживающей кривой нет. В некоторых случаях анализ графического изображения имеющихся данных, а также понимания механизма процесса помогают установить вид аналитической зависимости.
Значительное число зависимостей, встречающихся в практике научных исследований, можно описать следующими уравнениями: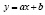 
(линейная), 
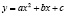(квадратичная), 
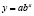(показательная), 
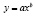(степенная) и 
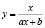(обратная зависимость). Показательную и степенную зависимости приводят к линейному виду путем логарифмирования обоих частей уравнений, обратную – с помощью замены.
Квадратичная зависимость обычно определяется из графических соображений. Для выбора между линейной, показательной и степенной или обратной зависимостями можно воспользоваться тем фактом, что для прямой величина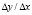 
есть постоянная и равная угловому коэффициенту прямой.
Технику выбора функциональной зависимости мы применили к решению следующей задачи. Торговое предприятие имеет сеть, состоящую из 12 магазинов. Необходимо установить зависимость размера годового товарооборота y (млн.руб) от торговой площади магазина x (тыс.м2).
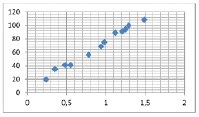
Используя имеющиеся статистические данные, произвели следующие вычисления с помощью программы Excel.
|
n |
x |
y |
|
|
|
|
|
1 |
0,24 |
19,76 |
̶ |
̶ |
̶ |
̶ |
|
2 |
0,35 |
35,09 |
139,36364 |
2,26724 |
1,522039 |
-0,01974 |
|
3 |
0,48 |
40,95 |
45,076923 |
0,515927 |
0,488948 |
0,01344 |
|
4 |
0,55 |
41,08 |
1,8571429 |
0,019665 |
0,023283 |
0,023813 |
|
5 |
0,78 |
56,29 |
66,130435 |
0,594786 |
0,901596 |
0,002036 |
|
6 |
0,94 |
68,51 |
76,375 |
0,533267 |
1,052935 |
-0,00085 |
|
7 |
0,98 |
75,01 |
162,5 |
0,98413 |
2,175086 |
-0,01639 |
|
8 |
1,12 |
89,05 |
100,28571 |
0,532248 |
1,284916 |
-0,00348 |
|
9 |
1,21 |
91,13 |
23,111111 |
0,111416 |
0,298726 |
0,007784 |
|
10 |
1,25 |
94,26 |
78,25 |
0,366652 |
1,038332 |
-0,00041 |
|
11 |
1,29 |
99,84 |
139,5 |
0,624428 |
1,825855 |
-0,00851 |
|
12 |
1,49 |
108,6 |
43,55 |
0,181626 |
0,580308 |
0,004029 |
|
Вид зависимости: |
линейная |
показательная |
степенная |
обратная |
||
Из таблицы видно, что наиболее близким к константе является столбец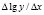 
, отвечающей показательной зависимости. Следовательно, зависимость товарооборота от площади может быть описана уравнением: y=abx.
Таким образом, если неизвестен характер зависимости между данными величинами x и y, то вид сглаживающей кривой является произвольным. Удачный выбор эмпирической формулы в значительной мере зависит от знаний исследователя в предметной области, используя которые он может указать класс функций из теоретических соображений. В других случаях одним из вариантов выбора является графическое изображение полученных данных и установления сходства с образцами известных кривых (визуальный способ). Другой вариант, как теоретически обоснованный выбор функциональной зависимости – это предложенный выше метод. Главным достоинством данной техники выбора сглаживающей кривой является ее простота и удобность использования.
Библиографическая ссылка
Давыдов А.С., Дьяконова К.С., Матвеева Т.А., Светличная В.Б. ВЫБОР ФУНКЦИОНАЛЬНОЙ ЗАВИСИМОСТИ СГЛАЖИВАЮЩЕЙ КРИВОЙ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ // Современные наукоемкие технологии. – 2014. – № 5-2. – С. 190-191;URL: https://top-technologies.ru/ru/article/view?id=34063 (дата обращения: 22.11.2024).