Магнитные жидкости являются уникальными средами способными достаточно сильно намагничиваться в магнитных полях небольшой напряженности при сохранении ими текучести. Сочетание данных свойств магнитных жидкостей открывает большие перспективы их практического применения. Большой интерес ученых и инженеров из разных стран к исследованию процессов теплообмена в кипящих магнитных жидкостях, связан с перспективой применения их в качестве управляемой при помощи магнитного поля закалочной среды, а также с возможным применением в качестве теплоносителя в теплообменных аппаратах и тепловых устройствах. Особого внимания, с точки зрения анализа теплообмена в кипящих жидкостях, в том числе и магнитных, заслуживает исследование процессов роста и отрыва пузырьков пара.
Существует несколько методов позволяющих измерять частоту отрыва и объем пузырьков пара при кипени жидкостей [1, 2]. Фотографический метод пригоден для исследования кипения прозрачных жидкостей и не пригоден для магнитных жидкостей, которые непрозрачны. Индукционный метод позволяют измерять частоту отрыва пузырьков пара при кипени, в том числе, и непрозрачных жидкостей, однако не позволяют оценить изменение формы и объема пузырьков пара при воздействии внешних магнитных полей.
Возможной альтернативой данным методам, применительно к магнитным жидкостям, является математическое моделирование процессов роста и отрыва парового пузырька при кипении магнитной жидкости во внешнем магнитном поле.
Рассчитаем равновесную форму капли магнитной жидкости находящейся на горизонтальной пластине в объеме немагнитной жидкости во внешнем однородном магнитном поле. Условие равновесия границы раздела намагничивающаяся жидкость-немагнитная среда во внешнем магнитном поле может быть описано уравнением [3]:
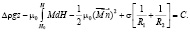(1)
Здесь z – вертикальная координата точки на поверхности капли, отсчитываемая от нижней части капли, R1 и R2 – радиусы кривизны поверхности раздела намагничивающаяся жидкость–немагнитная среда, определяемые выражениям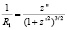и
и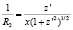 
,
µ0 – магнитная постоянная,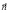 
– единичный вектор нормали к межфазной поверхности, С – постоянная величина. Первое слагаемое в выражении (1) – гидростатическое давление, второе и третье слагаемые – давления, обусловленные магнитным полем и скачком давления на границе раздела магнитная-немагнитная среда.
Рассмотрим случай, когда капля находится во внешнем однородном магнитном поле направленном горизонтально. Так как при больших высотах z капли ее форма слабо отличается от цилиндрической, то в этом случае можно допустить, что распределение магнитного поля на границе капли магнитной жидкости удовлетворяет соотношениям, справедливым для бесконечного цилиндра:
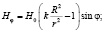
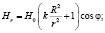
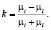(2)
Здесь 
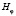и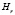 
– угловая и радиальная компоненты магнитного поля в цилиндрической системе координат, φ – полярный угол, отсчитываемый от направления внешнего магнитного поля 
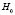, R – радиус цилиндра, r – расстояние от оси цилиндра до точки, в которой определяются компоненты магнитного поля. С учетом данного распределения поля, проекция уравнения (1) на плоскость xOz декартовой системы координат примет вид:
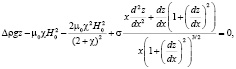(3)
на плоскость yOz:
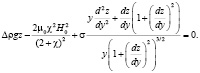(4)
Уравнения (3) и (4), описывающие форму капли МЖ во внешнем горизонтальном магнитном поле в двух взаимно перпендикулярных плоскостях, решались численно. На рис. 1 показаны интегральные кривые решения уравнения (3), описывающие форму капли магнитной жидкости в плоскости xOz.
Расчеты проводились для капли высотой z=0,012 м., при разных значениях напряженности магнитного поля. Устойчивые решения уравнения (3) удалось получить в интервале напряженности магнитного поля от 0 до 1,3 кА/м, для уравнения 6 в интервале от 0 до 2 кА/м. При увеличении величины напряженности поля выше указанных значений, решение становилось неустойчивым.
По представленным на рисунке зависимостям, видно, что ширина основания капли существенно возрастает c увеличением напряженности горизонтального магнитного поля. Так в поле напряженностью 1,3 кА/м ширина основания капли оказывается более чем в два раза больше, чем в случае отсутствия внешнего магнитного поля.
На рис. 2 изображены интегральные кривые уравнения (6), описывающие форму капли магнитной жидкости в горизонтальном магнитном поле в интервале напряженности от 0 до 2 кА/м в плоскости yOz.
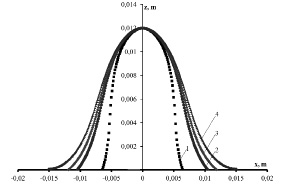
Рис. 1. Изменение формы капли магнитной жидкости высотой z=0,012 м в горизонтальном магнитном поле в проекции на плоскость xOz: 1 – 0 кА/м, 2 – 1 кА/м, 3 – 1,2 кА/м, 4 – 1,3 кА/м
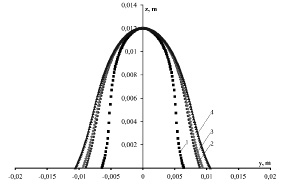
Рис. 2. Изменение формы капли магнитной жидкости высотой z=0,012 м в горизонтальном магнитном поле в проекции на плоскость yOz: 1 – 0 кА/м, 2 – 0,6 кА/м, 3 – 1,2 кА/м, 4 – 2 кА/м
Из рис. 2 видно, что с увеличением напряженности магнитного поля ширина основания капли в плоскости yOz также увеличивается, но в меньшей степени, чем в плоскости xOz, в которой лежал вектор магнитного поля. Таким образом, решения уравнений (3) и (4) показывают, что ширина основания капли магнитной жидкости увеличивается не только вдоль плоскости параллельной направлению действия силовых линий магнитного поля (плоскость xOz), но и в плоскости к ней перпендикулярной (плоскость yOz). Отношение ширины основания капли в проекциях на плоскости xOz и yOz меняется от 1 до 1,33, при изменении величины магнитного поля от 0 до 1,3 кА/м. Т.е. в отсутствие магнитного поля, поперечными сечениями капли будут являться окружности. При включении же магнитного поля капля вытягивается в обоих направлениях, и поперечные сечения капли приобретают эллипсоидальную форму.
Важно отметить, что, несмотря на то, что рост капли магнитной жидкости на горизонтальной поверхности, в экспериментах, происходит за счет поступления магнитной жидкости через отверстие в пластине, а рост пузырька пара при кипении магнитной жидкости происходил за счет испарения со всей поверхности раздела пар-жидкость, есть все основания считать, что процессы роста и формирования капли и пузырька качественно и количественно очень близки. Действительно, характерные времена роста и отрыва капель, в проводимых экспериментах, и пузырьков пара, одинаковы (порядка 1 сек.). Это означает, что инерционные силы и силы гидравлического сопротивления, возникающие при росте и отрыве капель и пузырьков, практически не различаются. Кроме того, слабо отличаются силы, влияющие на размеры и форму пузырька пара и капли магнитной жидкости, описываемые уравнением (2), так как величины входящие в это уравнение, в «холодном» для капли и в «горячем» для пузырька случае, разнятся менее чем на 30 %. Сказанное дает основание утверждать, что эксперименты по наблюдению за ростом и отрывом капли магнитной жидкости в немагнитной среде, адекватно описывают поведение пузырька пара при кипении магнитной жидкости.
Таким образом, теоретически определена величина деформации основания капли магнитной жидкости на горизонтальной поверхности в магнитном поле и дано объяснение влиянию магнитного поля на процессы образования, роста и отрыва капель магнитной жидкости в объеме немагнитной среды и пузырьков пара в намагничивающейся жидкости. Показано, что внешнее горизонтальное магнитное поле, изменяя периметр основания капли магнитной жидкости изменяет и время роста, отрывной диаметр и частоту отрыва капли МЖ от горизонтальной поверхности. Эти результаты дают основание считать, что аналогичные процессы будут наблюдаться и при образовании, росте и отрыве пузырьков пара при кипении магнитной жидкости в магнитном поле.
Работа выполнялась при финансовой поддержке РФФИ (грант № 14-01-00056).
Библиографическая ссылка
Яновский А.А., Спасибов А.С. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССОВ В КИПЯЩИХ НАМАГНИЧИВАЮЩИХСЯ СРЕДАХ // Современные наукоемкие технологии. – 2014. – № 5-2. – С. 183-186;URL: https://top-technologies.ru/ru/article/view?id=34057 (дата обращения: 22.11.2024).