Спрос в математическом смысле понимается как зависимость между ценой (P) и количеством товара (Q), который покупатели могут и желают приобрести по определенной цене, в определенный промежуток времени.
Спрос с точки зрения экономики это есть платежеспособная надобность покупателей в этом товаре при данной цене. Спрос характеризуется величиной спроса – количеством товаров, которое покупатели готовы приобрести по данной цене. Его величина показывает, что покупатели готовы купить такое количество товаров, но это не значит, что сделки действительно состоятся т.к. это зависит от ряда экономических факторов. Например, производители могут оказаться не в состоянии выпустить подобное количество товара. Под словом «готовы» понимается то, что у них есть потребность и наличие необходимых денежных средств для покупки товара в данном количестве. Можно рассмотреть как спрос конкретного покупателя, так и спрос всех покупателей, присутствующих на рынке. В экономике изучается общая величина спроса, так как конкретного покупателя зависит от личных предпочтений покупателя и не отражает действительной картины, сложившейся на рынке. Например, конкретный покупатель может не испытывать нужды в каком-либо товаре (например, самокате) но, на рынке спрос на этот товар будет существовать. Как правило, спрос на товар подчиняется закону спроса.
Прогнозирование спроса – это предсказание развития рынка во времени на основе изучения причинно-следственных связей, тенденций и закономерностей.
Прогнозирование спроса исполнять роль научно доказанного предвидение формирования платежеспособных потребностей населения на товары и услуги. При прогнозировании микроспроса распространенными являются следующие методы: с использованием структурных моделей; с использованием коэффициента эластичности спроса; экономико-математические.
Экономико-математические методы предлагают применение авторегрессионных, трендовых и факторных моделей.
Трендовые модели употребляются только если спрос является функцией времени: Y=f(t), где t – фактор времени; Y – фактор времени- показатель спроса. Эта зависимость описывает динамическое развитие спроса во времени. Формы зависимости спроса от времени могут быть различными. Существуют несколько видов прогнозирования спроса в экономике при помощи математического моделирования
Так же существуют следующие виды прогнозирования в зависимости от временного периода: оперативное (до 1 месяца); краткосрочное (от 1 до 2 лет); среднесрочное (от 2 до 5 лет); долгосрочное (от 5 до 10 лет).
Прямолинейная форма связи имеет вид: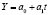 
где Y – показатель спроса; t – время; а0 а1 – параметры уравнения. Для определения параметров уравнения ад и а, в данном случае нужно решить следующую систему уравнений:
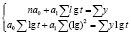
Применение данной модели предполагает снижение в динамическом ряду как абсолютных, так и относительных приростов спроса. Показательная форма связи имеет вид: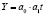 
. Для нахождения параметров уравнения а0 и а1 нужно решить следующую систему уравнений:
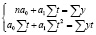
Использование предоставленной модели полагает приблизительно одинаковые показатели абсолютных приростов в динамическом ряду при снижении относительных темпов прироста.
Логарифмическая форма связи имеет вид: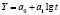 
. Для определения параметров уравнения а0 и а1 нужно решить следующую систему уравнений:
.
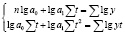Применение данной модели предполагает примерно постоянные относительные темпы прироста показателей спроса в динамическом ряду. Параболическая форма связи имеет вид: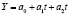 
. Для определения параметров уравнения а0, а1, а2 нужно решить следующую систему уравнений:
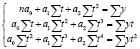
Необходимо оценить модель, рассчитав среднюю ошибку аппроксимации:
,
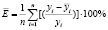где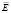 
– ошибка аппроксимации; 
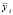– теоретические показатели ряда динамики, рассчитанные по модели; уi – эмпирические показатели ряда динамики; n – количество показателей в динамическом ряду.
Прогноз на основе рассчитанной модели может иметь смысл, если отклонение теоретических значений показателей спроса (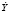
) от эмпирических (Y) в каждом конкретном случае не будет составлять больше 3-5 %, при этом средний процент отклонений также не должен быть больше 3-5 %.
Если отклонения и ошибка аппроксимации будут находиться в пределах нормы, то это значит, что предоставленную модель можно применять для прогнозирования. Для этого надо задать значение t для прогнозируемого периода и, подставив это значение в уравнение, рассчитать показатель Y для прогнозируемого периода.
Факторные экономико-математические модели полагают, что спрос является функцией нескольких факторов. В виде факторов могут быть цены, совокупный объем спроса, объем реализации заменяемого товара и др. Y=f(x), где Y – показатель спроса; х – фактор.
Зависимость характеризует изменение развития спроса в связи с динамикой выбранных факторов. В практике существуют разнообразные формы зависимости. Методика использования факторных моделей подобна рассмотренной методике трендовых моделей, только в качестве фактора берется не время (t), а другой показатель (х). Используются различные формы криволинейной зависимости (параболы, гиперболы, логарифмические и др.).
Разновидностью экономико-математических методов при прогнозировании спроса является авторегрессионная модель, которая имеет вид: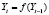 
, где Y –показатель спроса отчетного периода; Yi-1 – показатель спроса за предшествующий период.
Зависимость характеризует связь показателей отчетного периода с предыдущим. Форма связи имеет вид: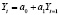 
, где Y – показатель спроса в отчетном периоде; Yt-1 – показатель спроса в предшествующем периоде; а0, а1 – параметры уравнения.
Для определения параметров уравнения а0 и а1 нужно решить следующую систему уравнений:
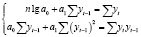
Для целей прогнозирования нам также необходимо оценить данную модель с точки зрения соответствия теоретических значений эмпирическим. Сложность использования для прогнозирования спроса разобранных моделей состоит в том, что довольно тяжело получить оперативную и статистическую информацию о реализации, как отдельных товаров, так и отдельных товарных групп на предприятиях торговли. Модель может быть применена при прогнозировании, если среднее значение отклонений будет равное не больше 3 – 5 %. В настоящее время отсутствует официальная статистическая отчетность о реализации по товарным группам. Однако предприятия торговли и общественного питания, имея современные средства обработки предоставляемых данных, такой информацией располагают, а, значит, могут вводить, разрабатывать и использовать соответствующие программы для прогноза реализации как в целом по отдельным группам товаров, так и по предприятию и даже отдельным товарам. Способность спроса повышаться или понижаться под влиянием воздействия различных факторов называется эластичностью спроса. Наиболее легким и приемлемым методом прогнозирования спроса для оперативных и краткосрочных целей является использование коэффициента эластичности.
Для количественного измерения воздействия какого-либо фактора на спрос применяют коэффициент эластичности. Коэффициент эластичности спроса – это показатель, характеризующий сравнительное изменение спроса под воздействием изменения фактора. Коэффициент эластичности можно рассчитать по формуле
,
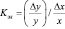где Кэл – коэффициент эластичности; ∆y – изменение спроса в отчетном периоде по сравнению с базисным; х – показатель фактора в базисном периоде; ∆x – изменение фактора в отчетном периоде по сравнению с базисным; у – показатель спроса в базисном периоде.
При прогнозировании спроса как фактора могут выступать спрос, цены в целом по предприятию, спрос на другой товар, на уровне региона – доходы на душу населения. Коэффициент эластичности показывает, на сколько процентов изменится спрос (Y) при изменении фактора (Х) на 1 процент. При расчете коэффициента эластичности изменение спроса (∆y –) и выбранного фактора (∆x) должно быть проанализировано не менее чем за 2-3 периода в ряду динамики. Показатели Y и X могут быть выражены как в относительных, так и в абсолютных показателях. Если показатели Y и X в базисном периоде равны 100 %, то формула коэффициента эластичности будет иметь следующий вид: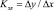 
Рассчитанный коэффициент эластичности может быть использован для краткосрочного прогнозирования если известно, на сколько изменится фактор в прогнозируемом периоде 
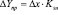, где ∆Yпр – изменение спроса в прогнозируемом периоде; ∆x – изменение фактора в прогнозируемом периоде; Кэл – коэффициент эластичности между спросом и выбранным фактором. По этой формуле можно рассчитать, на сколько процентов изменится последнее значение в ряду динамики и спрос в прогнозируемом периоде. После чего можно установить объем спроса в прогнозируемом периоде:
,
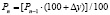где Рn – объем спроса в прогнозируемом периоде; Рn-1 – объем спроса в последнем периоде до прогноза.
Рассмотрим пример применения математического моделирования при прогнозировании спроса.
Имеется динамический ряд показателей.
|
Периоды |
Общий объем реализованного спроса по предприятию (Х), цепной темп роста, % |
Спрос на группу А(Y), цепной темп роста, % |
||
|
I вариант |
II вариант |
I вариант |
II вариант |
|
|
Базисный |
99,0 |
99,0 |
99,0 |
99,0 |
|
Предшествующий |
103,0 |
103,0 |
104,0 |
102,0 |
|
Отчетный |
106,0 |
106,0 |
108,0 |
105,0 |
Для I варианта
,
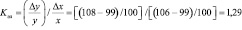или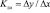 
= [(108-99)/(106-99)]=9/7=1,29.
Это значит, что при повышении совокупного объема спроса по предприятию на 1 % спрос на группу А растет на 1,29 %, то есть быстрее, чем общий объем реализованного спроса. Для II варианта
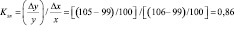или
.
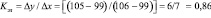Это означает, что при увеличении общего объема реализованного спроса в целом по предприятию на 1 % спрос на группу А растет на 0,86 %, т.е. медленнее, чем общий объем реализованного спроса. По имеющимся прогнозам, в планируемом периоде общий объем реализованного спроса по предприятию увеличится на 3 %. Тогда спрос на группу А в планируемом периоде возрастет: в 1 варианте – на 3,87 % (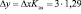
); во 2 варианте – на 2,58 % (
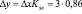). Если учесть, что в отчетном периоде объем реализации по группе А составил 1500 руб., в прогнозируемом периоде возможный объем спроса по данной группе может составить: в 1 варианте – 1558 руб. 
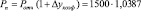; во 2 варианте – 1519 руб. 
.
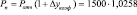При прогнозировании спроса могут быть применены и структурные модели, образованные на данных бюджетной статистики. В корне разработки таких моделей находятся данные опросов потребителей, при этом потребности группируются по выбранным признакам. Структурная модель имеет вид:
,
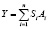где Y – показатель спроса; Аi – предпочтительный набор потребностей в i-й группе; Si – число потребителей в i-й группе; n – число групп потребителей. Допустим, что произведена первичная группировка потребителей по уровню среднего дохода на душу населения. Все опрошенные были распределены на 4 группы. Затем на основании опроса определяется спрос на какой-либо товар внутри каждой группы, либо предпочтение одного товара другим. Полученные данные применяются в формуле структурной модели.
Кроме рассмотренных нами методов могут применяться и другие, например экономико-статистические. В условиях рыночных отношений прогнозирование и изучение спроса на товары и услуги является необходимым условием благополучного функционирования предприятий торговли, общественного питания и сферы услуг.
Библиографическая ссылка
Шеин В.Г., Долгополова А.Ф. ОСОБЕННОСТИ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ПРИ ПРОГНОЗИРОВАНИИ СПРОСА // Современные наукоемкие технологии. – 2014. – № 5-2. – С. 181-183;URL: https://top-technologies.ru/ru/article/view?id=34056 (дата обращения: 23.11.2024).