Кривые второго порядка – это геометрическое место точек плоскости, прямоугольные координаты которых удовлетворяют уравнению вида
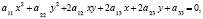
в котором как минимум один из коэффициентов не равен нулю.
Считается, что первым занялся изучением кривых второго порядка один из учеников Платона. Основываясь на траекториях отражения света, очертаниях растений и других природных явлениях, он предположил, что если взять две прямые, пересекающихся между собой, и начать вращать их вокруг угла ими же образованного, то получиться косинусовидная поверхность, которая при пересечении другой плоскостью станет образовывать сечение в виде различных геометрических фигур: эллипс, окружность, парабола, гипербола и др.
Потребовалось большое количество времени, прежде чем люди начали применять эти знания на практике.
Использование этих теорий началось примерно в XVII веке, когда люди усиленно изучали астрономию и выяснили, что планеты движутся по так называемым эллиптическим траекториям. А глобальное изучение кривых началось после выхода знаменитой книги Р. Декарта «Геометрия», в которой были опубликованы основы метода координат.
Открытие метода координат имело особо важное значение не только в математике, но и в физике, механике, астрономии, оптике и других дисциплинах.
Способы образования кривых
1. Кривая как линия пересечения данной поверхности плоскостью, положение которой определено. Этот способ изучался греческими математиками, которые определяли кривые второго порядка как сечение конуса.
2. Кривая как геометрическое место точек, обладающих данным свойством. Самый распространённый способ. При этом способе кривая рассматривается как геометрическое место точек, сохраняющее отношение расстояний от данной точки до прямой.
3. Кривая определяется как траектория точки, характер движения которой обусловлен тем или иным образом. В данном способе кривая имеет траекторию точки, движущейся одновременно в двух направлениях. Одно направление по прямой, другое по окружности.
4. Образование линий по способу сопряжения проективно соответствующих элементов. Этот способ рассматривают в курсе проективной геометрии, так как он является одним из последних. В его основе лежит идея соответствия проективных пучков или прямых.
Существуют два вида кривых второго порядка: невырожденные и вырожденные.
К невырожденным и относятся: эллипс, гипербола, парабола.
Как мы уже выяснили, кривой второго порядка является линия, определяющаяся уравнением:
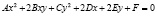
где A, B, C, D, E, F – действительные числа.
В зависимости от числовых значений A, B, C – получают различные виды кривых.
Уравнения геометрических фигур:
1. Каноническое уравнение окружности:
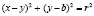
В случае, когда центр окружности совпадает с началом координат, уравнение имеет вид:
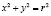
2. Каноническое уравнение эллипса:
.
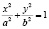Если центр эллипса находится в какой-либо точке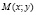 
, то для этого условия существует формула:
+ 
.
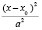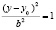3. Каноническое уравнение гиперболы:
.
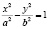4. Каноническое уравнение параболы:
.
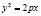При этом число p>0 (расстояние от фокуса до директрисы)- фокальный параметр.
Задачи в аналитической геометрии решаются с помощью кривых второго порядка.
Установить вид кривой
.
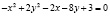Решение: Данное уравнение может описывать гиперболу. Выделим полные квадраты по переменным x,y. Для переменной x получаем квадрат суммы, для переменной y – квадрат разности
;
;
;
;
;
.
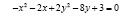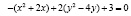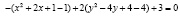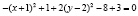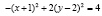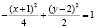Это уравнение описывает гиперболу, центр симметрии которой находится в точке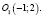 
Докажем это, введя обозначения 
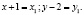Уравнения новых координатных осей 
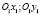имеют вид
.
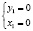Относительно старой системы координат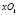 
новые оси записываются уравнениями:
; 
.
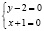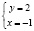В новой системе координат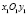 
заданное уравнение принимает канонический вид:
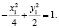
Это уравнение описывает гиперболу. Для более точного построения искомого графика найдем точки пересечения графика заданной гиперболы с координатными осями старой системы координат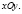 
Точки пересечения графика гиперболы с осью 
=> 
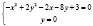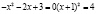
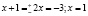
Точки пересечения графика гиперболы с осью
=>
.
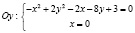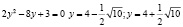Всё, что нужно для построения графика найдено.
Кривые второго порядка играют особую роль в геометрии. На них основываются знаменитые Теорема Паскаля и Теорема Брианшона.
В современном мире кривые второго порядка также используют в профессии закройщика. Конструирование одежды основывается на построении кривых и определении положения точек на дугах.
Библиографическая ссылка
Серикова В.С., Родина Е.В. КРИВЫЕ ВТОРОГО ПОРЯДКА // Современные наукоемкие технологии. – 2014. – № 5-2. – С. 175-177;URL: https://top-technologies.ru/ru/article/view?id=34052 (дата обращения: 18.04.2024).