Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Файлы
• Литература

Светличная В.Ю. 1 Орехова Н.В. 1 Мелешко С.В. 1

---

1 Ставропольский государственный аграрный университет

Статья в формате PDF

1075 KB

1. Мамаев И.И., Бондаренко В.В. Моделирование экономических процессов с использованием методов линейной алгебры // Аграрная наука, творчество, рост. – Ставрополь, изД-во «АГРУС», 2013. – Т.1,Ч.1. – C. 286.

2. Кострикин А.И., Манин Ю.И. Линейная алгебра и геометрия. – СПб.: Лань 2005.

3. Кремер Н.Ш. Высшая математика для экономистов. – Изд-во ЮНИТИ – ДАНА. М., 2007.

4. Сизова С.А., Мурдугова В.Ю., Мелешко С.В. Линейное программирование как область математического программирования при решении экономических задач // Teoretical & Applied Science. Международный научный журнал по материалам международной научно-практической конференции «World of Science», 30.06.2013, Hamburg, Germany. – №6, 2013. С. 16-20.

5. Цысь Ю.В., Долгополова А.Ф. Элементы линейной алгебры и их применение при решении экономических задач // Современные наукоемкие технологии. – 2013.– №6. – С.91-93.

В современное время математика интенсивно проникает в другие науки: во многом это происходит благодаря тому, что математики разделяется на ряд самостоятельных областей. Математический язык универсален, что является объективным отражением универсальности законов окружающего нас мира.

Экономика, как наука об основных причинах функционирования и улучшения общества, пользуется различными количественными характеристиками, а потому включает в себя множество математических методов.

Линейная алгебра неразрывно связана с экономикой. Одним из основных методов решения многих экономических задач является применение элементов алгебры матриц. Наиболее актуальным этот вопрос считается при разработке и использовании баз данных: при работе с ними почти весь материал содержится и обрабатывается в матричной форме. Таким образом, использование элементов линейной алгебры в значительной степени упрощает методы решения многих задач экономики.

Решение представленных заданий матричным способом нередко применяется в экономической деятельности. Это говорит о том, что основная часть математических процессов экономики закрепляется в наиболее простой, а главное – компактной матричной форме. Некоторые экономические зависимости удобно записывать в виде матриц.

В пример приведем таблицу распределения ресурсов по отдельным отраслям экономики (усл. ед.):

Эти данные можно представить в удобной форме в виде матрицы распределения ресурсов по отраслям:

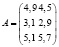
В данном примере, матричный элемент а11= 4,9 показывает, какое количество электроэнергии потребляет промышленность, а элемент а22= 2,9 – количество трудовых ресурсов в сельском хозяйстве.

Используя матрицы можно вычислить стоимость затрат сырья на единицу продукции, а также общую стоимость сырья.

Например, на предприятии производится продукция трех видов: P1, P2, P3 и используется сырье двух типов: S1, S2. Нормы расхода сырья представлены матрицей

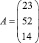
Каждый элемент 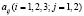определяет, сколько единиц сырья j-го типа затрачено на производстве – единицы продукции i-го вида. Порядок выпуска продукции отражен матрицей-строкой 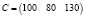, стоимость единицы каждого типа сырья (ден.ед.) – матрицей-столбцом:

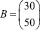
Решение 1.1.

Итак, затраты первого сырья составляют:

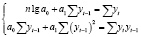ед.

и 2-го – ,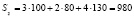

поэтому матрицу-строку затрат сырья S можно представить как произведение:

.

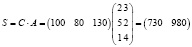Тогда совместная стоимость сырья 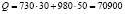денежных единиц, может быть записана в матричном виде:

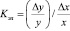
Общую стоимость сырья можно рассчитать и в другом порядке: вначале рассчитаем матрицу стоимостей затрат сырья на единицу продукции, т.е. матрицу:

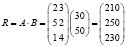
а затем общую стоимость сырья:

.

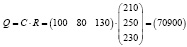Также наиболее широкое распространение в экономике получили системы линейных уравнений. С их помощью, возможно, решить множество экономических вопросов.

В пример можно привести следующую задачу.

Обувная фабрика специализируется по выпуску изделий трех видов: сапог, кроссовок и ботинок; при этом используется сырье трех типов: S1, S2, S3. Нормы расхода каждого из них на одну пару обуви и объем расхода сырья на 1 день заданы таблицей:

Необходимо найти ежедневный объем выпуска каждого вида обуви.

Решение 1.

Пусть ежедневно фабрика выпускает x1 пар сапог, x2 пар кроссовок, x3 пар ботинок. Тогда в соответствии с расходом сырья каждого вида имеем систему:

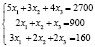
Решим систему методом Крамера

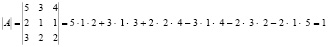
Следовательно, система имеет единственное решение:

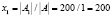
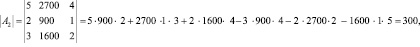
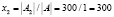
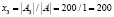
Значит, фабрика выпускает 200 пар сапог, 300 пар кроссовок и 200 пар ботинок.

Ответ: .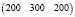

Итак, можно сделать вывод, что приведенные нами только самые основные задачи показывают, что знание элементов линейной алгебры, умение оперировать с матрицами и обратными матрицами, умение решать системы линейных уравнений позволяют решать реальные экономические задачи. Можно с уверенностью сказать, что применение математических методов в экономике, оправдает те надежды, которые на них возлагаются, вносит существенный вклад в экономическую теорию и хозяйственную практику.

Библиографическая ссылка